Chapter 12
Coupled
Oscillations
Two Coupled Harmonic Oscillators
Consider a system of two objects of mass M. The two objects are attached to two springs with spring constants k (see Figure 1). The interaction force between the masses is represented by a third spring with spring constant k12, which connects the two masses.
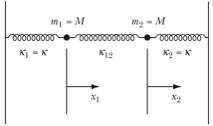
Figure 1. Two
coupled harmonic oscillators.
We will assume that when the masses
are in their equilibrium position, the springs are also in their equilibrium
positions. The force on the left
mass is equal to
![]()
The force on the right mass is equal
to
![]()
The equations of motion are thus
![]()
![]()
Since it is reasonable to assume
that the resulting motion has an oscillatory behavior, we consider following
trial functions:
![]()
![]()
Substituting these trial functions
into the equations of motion we obtain the following conditions:
![]()
![]()
These equations only will have a
non-trivial solution if
![]()
Note: the trivial solution is B1 = B2 = 0. The
requirement for a non-trivial solution requires that the angular frequency of
the system is equal to one of the following two characteristic frequencies (the
so called eigen frequencies):
![]()
![]()
For each of these frequencies, we
can now determine the amplitudes B1 and B2. Let us first consider the eigen
frequency w1. For this frequency we obtain the
following relations between B1 and B2:
![]()
or B1 = -B2. For the eigen frequency w2 we obtain the following
relations between B1 and B2:
![]()
or B1 = B2. The most general solution of the
coupled harmonic oscillator problem is thus
![]()
![]()
Another approach that can be used to
solve the coupled harmonic oscillator problem is to carry out a coordinate
transformation that decouples the coupled equations. Consider the two equations of motion. If we add them together we get
![]()
If we subtract from each other we
get
![]()
Based on these two equations it is
clear that in order to decouple the equations of motion we need to introduce
the following variables
![]()
![]()
The solutions to the decoupled
equations of motion are
![]()
![]()
where the frequencies are the
characteristic frequencies discussed before. Once we have these solutions we can determine the positions
of the masses as function of time:
![]()
![]()
We note that the solution h1 corresponds to an
asymmetric motion of the masses, while the solution h2 corresponds to an asymmetric motion of the
masses (see Figure 2). Since
higher frequencies correspond to higher energies, the asymmetric mode (out of
phase) has a higher energy.
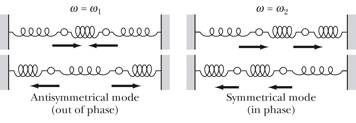
Figure 2. Normal
modes of oscillation.
Weak
Coupling
Coupled
oscillations, involving a weak coupling, are important to describe many
physical systems. For example, in
many solids, the force that tie the atoms to their equilibrium positions are
very much stronger than the inter-atomic coupling forces. In the example we discussed in the
pervious section, the weak coupling limit requires that k12 << k. In this approximation we can show (see
text book for details) that our solutions have a high-frequency component that
oscillates inside a slowly varying component (see Figure 3). The solutions are thus sinusoidal
functions with a slowly varying amplitude.
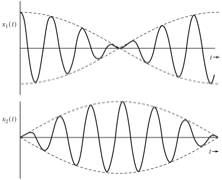
Figure 3. Examples of solution in the weak-coupling limit.
Example: Problem 12.1
Reconsider
the problem of two coupled oscillators discussion in Section 12.2 in the event
that the three springs all have different force constants. Find the two characteristic
frequencies, and compare the magnitudes with the natural frequencies of the two
oscillators in the absence of coupling.
![]()
The equations of motion are
![]() (1)
(1)
We attempt a solution of the form
![]() (2)
(2)
Substitution of (2) into (1) yields
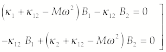 (3)
(3)
In order for a non-trivial solution to exist, the determinant
of coefficients of
![]() and
and
![]() must vanish.
This yields
must vanish.
This yields
![]() (4)
(4)
from which we obtain
![]() (5)
(5)
This result reduces to
![]() for the case
for the case
![]() (compare Eq.
(12.7)].
(compare Eq.
(12.7)].
If
![]() were held fixed,
the frequency of oscillation of
were held fixed,
the frequency of oscillation of
![]() would be
would be
![]() (6)
(6)
while in the reverse case,
![]() would oscillate with the frequency
would oscillate with the frequency
![]() (7)
(7)
Comparing (6) and (7) with the two frequencies,
![]() and
and
![]() , given by (5), we find
, given by (5), we find
![]()
![]() (8)
(8)
so that
![]() (9)
(9)
Similarly,
![]()
![]() (10)
(10)
so that
![]() (11)
(11)
If
![]() , then the ordering of the frequencies is
, then the ordering of the frequencies is
![]() (12)
(12)
Example: Problem 12.3
Two
identical harmonic oscillators (with masses M and natural frequencies w0)
are coupled such that by adding to the system a mass m, common to both oscillators, the equations of motion
become
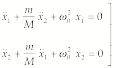
Solve this pair of coupled
equations, and obtain the frequencies of the normal modes of the system.
The equations of motion are
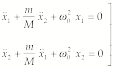 (1)
(1)
We try solutions of the form
![]() (2)
(2)
We require a non-trivial solution
(i.e., the determinant of the coefficients of
![]() and
and
![]() equal to zero),
and obtain
equal to zero),
and obtain
![]() (3)
(3)
so that
![]() (4)
(4)
and then
![]() (5)
(5)
Therefore, the frequencies of the normal modes are
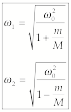 (6)
(6)
where
![]() corresponds to
the symmetric mode and
corresponds to
the symmetric mode and
![]() to the anti-symmetric
mode.
to the anti-symmetric
mode.
By inspection, one can see that the normal coordinates for this problem are the same as those for the example of Section 12.2. Another approach to find the normal coordinates is to try to find ways to add the two equations of motion in such a way that we get an uncoupled differential equation. Consider what happens when we multiply the first equation of motion by l and add it to the second equation of motion:
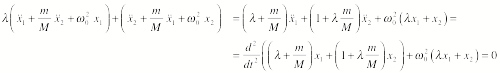
This will become an uncoupled equations if
![]()
This equation can only be correct if
![]()
and
![]()
Taking the last equation for g and substituting it into the second
to last equation we obtain
![]()
This shows that
![]()
and the normal coordinates are
proportional to x2 + x1 and x2 - x1.
General
Problem of Coupled Oscillations
The
results of our study of the coupled harmonic oscillator problem results in a
number of different observations:
o
The
coupling in a system with two degrees of freedom results in two characteristic
frequencies.
o
The
two characteristic frequencies in a system with two degree of freedom are
pushed towards lower and higher energies compared to the non-coupled frequency.
Let us now consider a system with n coupled oscillators. We can describe the state of this system in terms of n generalized coordinates qi. The configuration of the system will be described with
respect to the equilibrium state of the system (at equilibrium, the generalized
coordinates are 0, and the generalized velocity and acceleration are 0). The evolution of the system can be
described using Lagrange's equations:
![]()
The second term on the left-hand
side will contain terms that include the generalized velocity and the
generalized acceleration, and is thus equal to 0 at the equilibrium
position. Lagrange's equations
thus tells us that
![]()
However, since we know how to
express the kinetic energy of the system in terms of the generalized
coordinates we conclude that
![]()
where
![]()
For the potential energy U we conclude that
![]()
The potential energy can be expanded
around the equilibrium position using a Taylor series and we find that
![]()
where
![]()
We thus conclude that:
![]()
![]()
The equation of motion can now be
written as
![]()
The index k runs over all degrees of freedom of the system, and
we thus have n second order
differential equations. In order
to find the general solution we try a trial solution that exhibits the expected
oscillatory behavior:
![]()
With this solution, the equations of
motion become
![]()
This set of equations will only has
non-trivial solutions if the determinant of the coefficient must vanish:
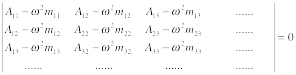
In general there will be n different values of the angular frequency. These frequencies are called the
characteristic frequencies or eigen frequencies. Depending on the coefficients, some of the characteristic
frequencies are the same (this phenomena is called degeneracy). For each eigen frequency we can
determine the ratio of the amplitudes; these amplitudes define an n-dimensional vector, also called the eigen
vector. Note: the eigen vector has
a pure harmonic time dependence.
The
general solution of the system is a linear combination of the solutions qi. Of course, it is only the real part of the solutions that is meaningful.
The
normal coordinates can be determined by finding the appropriate linear
combinations of solutions qi that oscillates at a single frequency. These normal coordinates are
![]()
The amplitude may be a complex
number. The normal coordinates
must satisfy the following relation
![]()
Since there are n equations of motion, we also expect to see n normal coordinates, and n decoupled equations of motion.
To
illustrate the detailed steps to be followed to solve a coupled oscillator
problem we will examine Example 12.4 from the textbook. In this example, the coupled pendulum
shown in Figure 4 is examined.
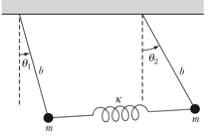
Figure 4. Coupled
pendulum of Example 12.4.
1.
Choose generalized coordinates. The proper generalized
coordinates in this problem are the angles q1 and q2. The kinetic and the potential energy of
the system can be easily expressed in terms of these angles. We make the assumption that the spring
is massless and there is thus no kinetic energy associated with the motion of
the spring. The kinetic energy of
the system is thus just equal to the kinetic energy of the two masses, and thus
equal to
![]()
The potential
energy of the system is the sum of the potential energy associated with the
change in the height of the masses and the potential energy associated with the
extension or compression of the spring. The total potential energy is thus equal to
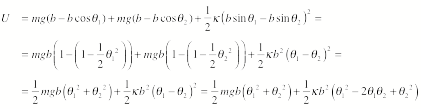
We have used the
small angle approximation in order to express the sin and cos of the angles in
terms of the angles.
2.
Determine the A and m tensors. In order to calculate these tensors we
use the expressions for T and U obtained in step 1. Since the kinetic energy obtained in step 1 does not contain
products of the generalized velocity of mass 1 and the generalized velocity of
mass 2, the mass tensor will be a diagonal tensor. We can see this by looking at the definition of the mass
tensor elements:
![]()
The mass tensor is
thus equal to
![]()
The A tensor is equal to
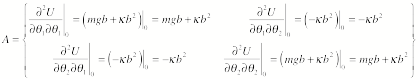
3.
Determine the eigen frequency and the eigen vectors. The
eigen frequencies can be determined by requiring that the determinant of the
coefficients of the equations of motions vanishes:
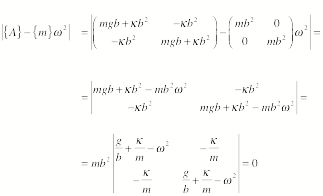
This requires that
![]()
or
![]()
The eigen
frequencies are thus equal to
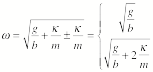
Consider the first
eigen frequency. For this frequency,
the eigen vector is (a11, a21). The equations of motion for this frequency are
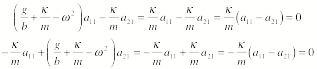
Each of these two
equations tells us that a11 = a21.
Since
the eigen vectors are orthogonal, we expect that the eigen vector for the
second eigen frequency is given by a12 = -a22. We come to the same conclusion if we
start from the equations of motion for that frequency and the eigen vector (a12, a22):
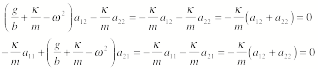
Each of these two
equations tells us that a12 =
-a22.
4.
Determine the scale factors required to match the initial conditions. In
this example, we do not need to match initial conditions (such as the initial
displacement or the initial velocity and we thus do not need to determine scale
factor).
5.
Determine the normal coordinates. The normal coordinates
are those coordinates that oscillate with a single frequency. In the current example we thus observe
the following normal coordinates:
![]()
![]()
Note: the constants
in these equations need to be adjusted to match the initial conditions.
The system will
carry out a motion with normal frequency 1 when h2 = 0. This requires that q1 = q2 and the motion is
symmetric. The system will carry out a motion with normal frequency 2 when h1 = 0. This requires that q1 = -q2 and the motion is
asymmetric.
Molecular
Vibrations
Our
theory of coupled oscillations has many important applications in molecular
physics. Each atom in a molecule
has 3 degrees of freedom, and if we are looking at a molecule with n atoms, we have a total of 3n degrees of freedom. Three different types of motion can be carried out by the atoms
in the molecule: translation (3 degrees of freedom), rotation (3 degrees of
freedom), and vibration (3n - 6
degrees of freedom).
Consider
a linear molecule (the equilibrium positions of all atoms are located along a
straight line) with n atoms. The number of degrees of freedom
associated with Vibrational motion is 3n – 5 since there are only 2 rotational degrees of
freedom. The vibrations in a
linear molecule can be longitudinal vibrations (there are n - 1 degrees of freedom associated with this type of
vibrations) and transverse vibrations (there are (3n - 5) - (n - 1) = (2n - 4) degrees of
freedom associated with this type of vibration). If the vibrations are planar vibrations (the motion of all
atoms is carried out in a single plane) we can specify any transverse vibration
in terms of vibrations in two mutually perpendicular planes. The characteristic frequencies in each
of these planes will be the same (symmetry) and the number of characteristic
frequencies will thus be equal to n - 2.
To
illustrate molecular vibrations let us consider the dynamics of a triatomic
molecule (see Figure 5).
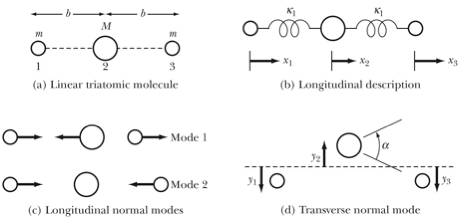
Figure 5. Vibrational motion of a linear triatomic molecule.
In order to determine the
vibrational modes of this system we look at the longitudinal and transversal
modes separately. Since we are not
interested in pure translational motion we can require that the center of mass
of the system is at rest. This
means that we do not have 3 independent position coordinates, but only 2. For example, we can eliminate the
position of the heavy atom:
![]()
In order to determine the normal
modes, we will follow the same procedure as we used in the previous example
(note: this differs from the approach used in the textbook).
1.
Choose generalized coordinates. The proper generalized
coordinates in this problem are the displacements x1 and x2. The kinetic and the potential energy of
the system can be easily expressed in terms of these displacements. The kinetic energy of the system is
thus just equal to the kinetic energy of the three atoms, and thus equal to
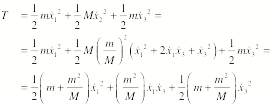
The potential
energy of the system is the sum of the potential energy associated with the
compression of the springs. The
total potential energy is thus equal to
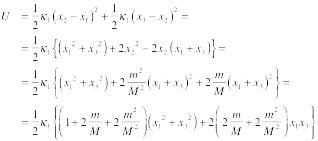
2.
Determine the A and m tensors. In order to calculate these tensors we
use the expressions for T and U obtained in step 1. Since the kinetic energy obtained in step 1 does not contain
products of the generalized velocity of mass 1 and the generalized velocity of
mass 2, the mass tensor will be a diagonal tensor. We can see this by looking at the definition of the mass
tensor elements:
![]()
The mass tensor is
thus equal to
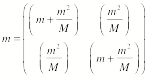
The A tensor is equal to
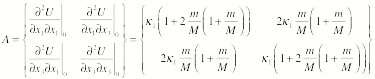
3.
Determine the eigen frequency and the eigen vectors. The
eigen frequencies can be determined by requiring that the determinant of the
coefficients of the equations of motions vanishes:
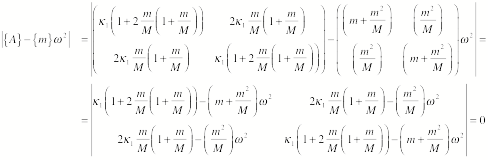
This requires that
![]()
or
![]()
Consider the two
signs. First the positive sign:
![]()
This is equivalent
to
![]()
or
![]()
Now consider the
negative sign:
![]()
This is equivalent
to
![]()
or
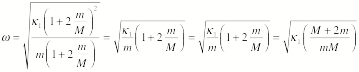
Consider the first
eigen frequency, and assume the corresponding eigen vector is (a11, a21). The
equations of motion for this frequency are
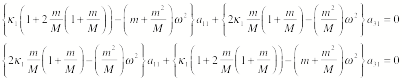
Substituting the
expression of the first eigen frequency in these equations we obtain for each
equation the following expression:
![]()
This equations
tells us that a11 = -a31. Since the eigen vectors are orthogonal, we expect that the eigen vector
for the second eigen frequency is given by a12 = a32.
4.
Determine the scale factors required to match the initial
conditions. In this example, we do not need to match initial conditions
(such as the initial displacement or the initial velocity and we thus do not
need to determine scale factor).
5.
Determine the normal coordinates. The normal coordinates
are those coordinates that oscillate with a single frequency. In the current example we thus observe
the following normal coordinates:
![]()
![]()
Note: the constants
in these equations need to be adjusted to match the initial conditions.
The system will
carry out a motion with normal frequency 1 when h2 = 0. This requires that x1 = -x3 and the motion is asymmetric. The system
will carry out a motion with normal frequency 2 when h1 = 0. This requires that x1 = x3 and the motion is symmetric.
Note: the normal
frequency 1 is equal to the frequency of a mass m on a spring whose other end remains fixed. This mode requires the central atom to remain fixed, and
this can be achieved when the motion is asymmetric since the forces exerted by
the two springs on the central mass cancel.
The transverse vibration of the
molecule can be specified in terms of a single parameter a. For this mode of vibration we will get a single
"uncoupled" differential equation with a single corresponding
characteristic frequency. The
calculation of this frequency is shown in detail in the text book and will not
be reproduced here.
Example: Problem 12.21
Three
oscillators of equal mass m are coupled
such that the potential energy of the system is given by
![]()
where
![]()
Find the eigen frequencies by
solving the secular equation. What
is the physical interpretation of the zero-frequency mode?
The tensors
![]() and
and
![]() are:
are:
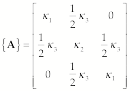 (1)
(1)
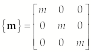 (2)
(2)
thus, the secular determinant is
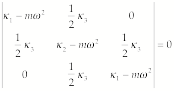 (3)
(3)
from which
![]() (4)
(4)
In order to find the roots of this equation, we first set
![]() and then factor:
and then factor:
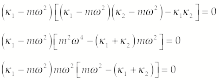 (5)
(5)
Therefore, the roots are
 (6)
(6)
Consider the case
![]() . The equation of motion is
. The equation of motion is
![]() (7)
(7)
so that
![]() (8)
(8)
with the solution
![]() (9)
(9)
That is, the zero-frequency mode corresponds to a translation of the system with oscillation.
The
Loaded String
A
good model of an elastic string is a string of particles of mass m, each separated by a distance d (see Figures 6 and 7). We will assume that the tension in the string is constant
and equal to t.
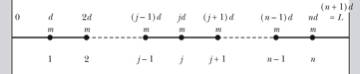
Figure 6. The
loaded string.
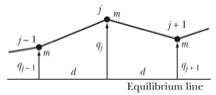
Figure 7. Calculation of the restoring force acting on mass j.
In examining this problem, we will
make the following assumptions:
·
The
masses can only move in the vertical direction (thus only the component of the
tension in the vertical direction matters).
·
The
potential energy of the system is the potential energy associated with the
tension in the string.
·
We
assume that the displacements from the equilibrium positions are small.
·
We
ignore the gravitational forces acting on the masses (and the associated
gravitational potential energy).
In order to calculate the force
acting on mass j we calculate the
vertical components due to the tension in the left and right section of the
string:

In the last step we have made the
assumption that the vertical displacement is small compared to the distance d. Since the force on mass j depends not only on the position of mass j but also on the position of masses j - 1 and j + 1. We can use the force on the n masses to obtain n coupled differential equations that we can try to
solve. Consider the following
trial function:
![]()
Substituting this function into our
differential equation we obtain
![]()
or
![]()
The amplitudes a can be complex. Based on the type of motion we expect the system to carry
out, we can try to parameterize the amplitude dependence on j in the following way:
![]()
where a is now a real number. Taking this expression for aj and substituting it into the previous equation we
obtain
![]()
This expression can be used to find
the following expression for the angular frequency:
![]()
or
![]()
Since there must be n eigen frequencies, we expect to find n distinct values of g.
Additional
constraints are imposed on the solution by requiring that the boundary
conditions are met:
·
a0 = 0: This condition requires that (note: we only consider the
real part of the amplitude)
![]()
or
![]()
·
an+1 = 0: This condition requires that
![]()
The argument of the
sin function must thus be an integer multiple of p:
![]()
or
![]()
where s = 1, 2, 3, …, n.
Since the boundary conditions
provide us with n different values of
the parameter g, we
expect that there will also be n unique
values of the angular frequency for this system:
![]()
where s = 1, 2, 3, …, n.
Putting
all the different pieces of information together we can now write down the
general solution of the loaded string problem:
![]()
and
![]()
We
can also use the Lagrangian method to find the normal modes of the system, but
as we will see, this approach is much less transparent than the approach just
used. In order to apply this
procedure we need to determine the kinetic energy and the potential of the
system in terms of the generalized coordinates. In this particular problem, the best choice for the
generalized coordinates is the vertical displacement of the masses. In terms of these displacements we can
write the kinetic energy as
![]()
In order to determine the potential
energy of the system, we first have to determine the potential energy of mass j. Since
we know the relation between the potential energy and the force, we can see
that the potential energy is equal to
![]()
Note: the index runs from j = 1 to j = n + 1. There are no masses at position 0 and
at position (n+1)d; these positions are the ends of the string. The displacement at these locations is
equal to 0.
Note: in order to verify that the
potential energy is correct, we need to show that its gradient is related to
the force on mass j:
![]()
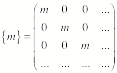
The mass tensor m for the system is given by
The potential tensor A for the system is given by
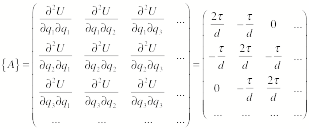
The eigen frequencies can now be
found by requiring that the secular determinant is equal to 0:
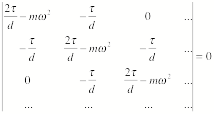
We can solve this equation for w but the results are more difficult
to interpret than the results obtained with out first approach.
Many important physics systems involved coupled oscillators. Coupled oscillators are oscillators connected in such a way that energy can be transferred between them. The motion of coupled oscillators can be complex, and does not have to be periodic. However, when the oscillators carry out complex motion, we can find a coordinate frame in which each oscillator oscillates with a very well defined frequency..
A solid is a good example of a system that can be described in terms of coupled oscillations. The atoms oscillate around their equilibrium positions, and the interaction between the atoms is responsible for the coupling. To start our study of coupled oscillations, we will assume that the forces involved are spring-like forces (the magnitude of the force is proportional to the magnitude of the displacement from equilibrium).