1. (50%) WeBWorK set # 5.
2. (25%) Consider a microscopic spring-mass system whose spring stiffness is k = 50 N/m and mass is m = 4 x 10-26 kg.
a. What is the smallest amount of vibrational energy that can be added to this system?
b. In a collection of microscopic oscillators, the temperature is high enough that the ground state and the first three excited states are occupied. What are the possible energies and wavelengths of the photons emitted by the oscillators.
3. (25%) Suppose we have reason to suspect that a certain quantum object has only three quantum states. When we excited such an object we observe that is emits electromagnetic radiation of three different energies: 2.48 eV (green), 1.91 eV (orange), and 0.57 eV (infrared). Propose two possible energy-level schemes for this system.
4. (Optional; 50% extra credit) From glowscript.org you can download a skeleton VPython code, DampedAndDriven, that simulates the motion of a harmonic oscillator exposed to both a damping and a driving force. In this problem we will study the resonance behavior of such a system in detail by focusing on a spring-mass system. The configuration to be studied is shown schematically in the figure below.
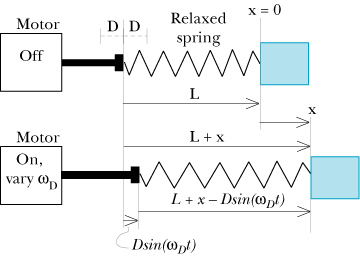 |
One
end of the spring is moved back and forth by a motor such that the
displacement from equilibrium of that end of the spring is given by D sin(wDt). Here, D is
the amplitude of the motion of the motor and wD is
the angular frequency of the motor; this frequency is adjustable. The natural frequency of the system, wF, is fixed and determined
by the spring constant k and
the mass m of the block: wF = √(k/m).
a. The python code you download from our webpage does not include the driving motion of the left end of the spring. Verify that without the driving force the angular frequency of the motion of the block is consistent with the natural frequency you expect to see, given the known spring constant and mass. You will see the effect of the damping force in your simulation, but we know that the frequency of the system should not be affected by the damping force (at least not for the case where the damping force is viscous, proportional to the velocity).
b. Modify the code to include the driving force. Turn off the friction force by setting uvisc to 0 and verify that the results of your simulations change qualitatively as you expect, based on what you know about driven harmonic motion (e.g., the steady-state frequency is equal to the driving frequency and the amplitude of the motion increases when the driving frequency approaches the natural frequency).
c. Turn the viscous damping force back on by setting uvisc to 0.003. Set the driving frequency to 90% of the natural frequency (wD = 0.90wF) and study the time evolution of the system. How long does it take before a steady state is reached? In the steady state, the energy dissipation per cycle is exactly equal to the energy input per cycle.
d. Vary the driving frequency in the range between 0 and 2.0wF with closely spaced values in the neighborhood of 1.0wF. For each driving frequency determine the steady-state amplitude and the phase shift (the difference in angle between the sinusoids for the motor and for the mass).
e. Sketch graphs of the steady-state amplitude and phase shifts as function of wD.
Send a summary of your study, including the graph, via email to Professor Wolfs (wolfs@pas.rochester.edu). Also submit the actual program , or a link to glowscript, via email to Professor Wolfs. The name of the files should start with hw05p04XXYYYYYYYY where XX are your initials and YYYYYYYY is your student id number. The subject of your email should be hw05p04XXYYYYYYYY.
Last updated on Thursday, June 6, 2024 7:52