Physics 141, Fall 2023.

1.     (50%) WeBWorK set # 3.

 

2.     (15%) There is no general analytical solution for the motion of a 3-body gravitational system.  However, there exists an analytical solution for the very special case shown in the Figure below.  In this Figure, three stars are shown, each of mass m, which move with the same speed in the plane of the page along a circle of radius r.  The three stars move in a clock-wise direction.  Calculate how long it will take for this system to make one complete revolution.

 

 

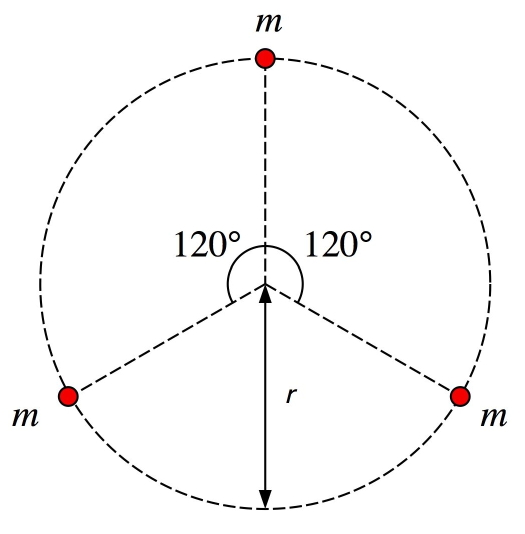3.     (20%) A hanging copper wire with a diameter of 2 mm has an initial length of 3 m and hangs vertically from the ceiling of your dorm room.  When a 5 kg mass is attached to its end, the wire stretches by 0.425 mm; when a 10 kg mass is attached to its end, the wire stretches by 0.85 mm.  The density of copper is 9 g/cm³ and one mole has a mass of 63 g.  Find the approximate value of the effective spring stiffness of the inter-atomic force.  Explain your analysis and any assumptions you may have made.

 

4.     (15%) In the software download area of the Physics 141 web site (located at http://teacher.pas.rochester.edu/phy141/Software/SoftwareIndex.htm) you will find two movies that shows someone tossing a ball in an elevator that is moving up (ElevatorMovie1.mov and ElevatorMovie2.mov).  Use Logger Pro to analyze the motion of the ball in both movies and answer the following questions:

a.     What is the acceleration of the ball in each toss?  In ElevatorMovie1.mov you will only be able to examine one toss, while in ElevatorMovie2.mov you will be able to examine multiple tosses.

b.     What can you say about the difference in the motion of the elevators in the two movies?

 

5.      (Optional; 25% extra credit) Place a spacecraft of mass 15000 kg at a location 10 Earth radii to the left of the center of the Earth and give it an initial velocity as shown in the Figure. 

 

 

Let it coast, subject only to the gravitational attraction of the Earth, whose mass is 6 × 10²⁴ kg.  Plot a trail behind the spacecraft so that you can see the shape of the trajectory.  At each step in the iteration, check for the spacecraft being closer than one Earth radius from the center of the Earth, and stop the program if that happens.

1. Predict what will happen when the initial speed of the spacecraft is zero.  Then try it.
2. Try various initial velocities.  What is the minimum speed required to go around the Earth without colliding?  This orbit can be shown to be an ellipse.
3. Cut the time step you used in your program by a factor of two and make sure that you essentially get the same trajectory seen in (2).  If there is a significant change in the trajectory, keep cutting the step size until you no longer see a change in the trajectory.  Repeat step (2) if your earlier step size was too large (resulting in poor accuracy and a strong dependence of the orbit in the step size).  On the other hand, if the orbit plots very slowly, you may have chosen a step size that is much smaller than necessary.  Try doubling the step size repeatedly until you start to see significant changes in the trajectory, then reduce the step size somewhat.
4. Using the step size that provides good accuracy, determine the launch speed that leads to a circular orbit.
5. Predict what will happen if the initial speed is somewhat greater than the speed that produces a circular orbit.  Now try it.
6. What is the minimum launch speed for which the spacecraft escapes, never coming back?
7. Try launching the spacecraft to the left, straight away from the Earth with the speed that produces a circular orbit in (4).
8. When launching to the left, what is the minimum launch speed for which the spacecraft escapes, never coming back.  Compare your answer with the results you obtained in (6)?

Submit the actual programs or a link to your public area of glowscript and your answers to the questions in pdf format via email to Professor Wolfs (wolfs@pas.rochester.edu).  The name of the file should be hw03p05XXYYYYYYYY.txt and hw03p05XXYYYYYYYY.pdf, where XX are your initials and YYYYYYYY is your student id number and the subject of your email should start with hw03p05XXYYYYYYYY.