When an object all of a sudden changes its velocity and/or direction, we can always find an interaction between that object and its surroundings that is responsible for this change. We state that the surroundings exert a force on the object studied. Under the influence of a force, an object will accelerate. All around us we observe that all moving objects will come eventually to rest, unless we apply a force to them. We need to keep pedaling if we want to keep a bicycle going with constant speed, we need to have our engine running if we want to keep driving with a speed of 55 miles/hour. In all these cases, friction will ultimately stop any moving object, unless the friction force is canceled by the force supplied by our legs, our engine, etc. If we reduce friction, the moving object will take longer to slow down, and the force needed to overcome the friction force will be less. In the limit of no friction, our object will keep moving with a constant velocity, and no force need to be applied. This conclusion is summarized in Newton's first law:
" Consider a body on which no net force acts. If the body is at rest, it will remain at rest. If the body is moving with constant velocity, it will continue to do so. "
If we exert the same force on several objects with different mass, we will observe different accelerations. For example, one can throw a baseball significantly further (and faster) than a ball of similar size made of lead. The unit of force is the Newton (N), and a force of 1 N is defined as the force that when applied to an object with a mass of 1 kg, produces an acceleration of 1 m/s^2. If we apply a force equal to 2 N, the corresponding acceleration is 2 m/s^2.
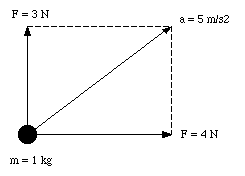
Experiments have shown that the force is a vector. This can be shown by demonstrating that the force has a magnitude and a direction. Suppose, we apply a force of 3 N to our standard object (mass 1 kg). The force is applied such that the resulting acceleration of 3 m/s^2 is upwards (positive y-direction). In addition, we apply a force of 4 N in the horizontal direction (this force is applied such that the standard object will accelerate with an acceleration of 4 m/s^2 in the direction of the positive x-axis if this is the only force applied). The situation is illustrated in Figure 1. If both forces are acting on the standard mass simultaneously, the acceleration of the object is measured to be 5 m/s^2, and the direction of the acceleration coincides with the direction of the vector sum of the two forces. The total force is 5 N and is equal to the magnitude of the sum vector of the two forces (if we assume that the direction of the force is equal to the direction of the acceleration). We conclude that indeed the force is a vector and that both the force and the corresponding acceleration have the same direction.

Figure 1. The Acceleration of the standard body under the influence of two forces.
The acceleration produced by a certain force depends on the mass of the object. The acceleration of an object with twice the mass of the standard mass under the influence of a certain force is half that of the acceleration of the standard mass due to the same force. The following list summarizes what we have learned so far about forces:
The conclusions are summarized in Newton's second law:'
![]()
where [Sigma]F is the vector sum of all forces acting on an object with
mass m, and ![]() is the resulting acceleration (note: the sum includes
only external forces). Newton's second law includes a formal statement of
Newton's first law: if there is no net force acting on an object ([Sigma]F
= 0 N) the acceleration is zero (and the velocity of the object is constant).
is the resulting acceleration (note: the sum includes
only external forces). Newton's second law includes a formal statement of
Newton's first law: if there is no net force acting on an object ([Sigma]F
= 0 N) the acceleration is zero (and the velocity of the object is constant).
© Frank L. H. Wolfs, University of Rochester, Rochester, NY 14627, USA
Last updated on Sunday, February 11, 2001 21:54