In a collision, strong mutual forces act between a few particles for a short time. These internal forces are significantly larger than any external forces during the time of the collision. The laws of conservation of linear momentum and energy, applied to the "before" and "after" situations, often allows us to predict the outcome of a collision. A great deal can be learned about the interactions between the colliding particles from the observed collision products.
Note:
A very important parameter that is often used in the description of collisions is the linear momentum of the objects involved. The linear momentum p of an object with mass m and velocity v is deined as
p = m v
The linear momentum is a vector. This means that it is characterized by both a magnitude and a direction. The direction of the linear momentum of an obejct is equal to the direction of the velocity of that object.
Under certain circumstances the linear momentum of a system is conserved. The linear momentum of a particle is related to the net force acting on that object. The rate of change of linear momentum of a particle is equal to the net force acting on the object, and is pointed in the direction of the force. If the net force acting on an object is zero, its linear momentum is constant (conservation of linear momentum).
Suppose a force F acts during a collision. The result of the collision force will be a change in the momentum of the particles involved. The amount of change depends not only on the average value of the force, but also on the time period during which it acts. The change in momentum dp is related to the collision force F as
![]()
The total change in the of momentum during the collision is given by
![]()
The total linear momentum p of a system of particles is defined as the vector sum of the individual linear momenta. If the net external force acting on a system of particles is zero, the linear momentum of the system is conserved.
Consider the collision shown in Figure 1. If there are no external forces acting on this system (consisting of the two masses) the total momentum of the system is conserved. The first class of collisions we will discuss are the elastic collisions. Collisions are called elastic collisions if the total kinetic energy of the system is conserved. This means that none of the energy associated with the motion of the objects involved in the collision is transferred into internal energy (like for example the energy associated with the deformation of the colliding objects).
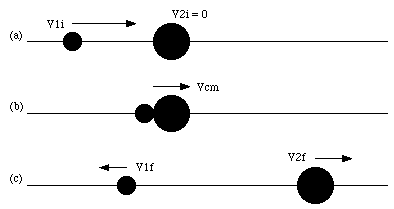
Figure 1. Collision in One-Dimension.
Using various conservation laws we can show that the final velocity of m1 is equal to
![]()
and the final velocity of mass m2 is equal to
![]()
It is clear that the velocity of m2 is always positive. The velocity of m1 can be either positive or negative, depending on the masses of the two objects: v1f is negative if m2 > m1, and positive if m2 < m1.
Some Special Cases
The previously derived equations show that in this case
v1f = 0 m/s
v2f = v1i
In head-on collisions, particles of equal mass simply exchange velocities.
Using the previously derived expressions for v1f and v2f we obtain
![]()
![]()
The projectile simply bounces back and the final velocity of the target will be a very small fraction of the initial velocity of the projectile.
Using the previously derived expressions for v1f and v2f we obtain
![]()
![]()
The velocity of the projectile is almost unchanged while the target will move with twice the initial velocity of the projectile.
If no external forces act on a system, its linear momentum is conserved. However, kinetic energy is not always conserved. An example of an inelastic collision is a collision in which the particles stick together (after the collisions). This type of a collision is a completely inelastic collision. The lost kinetic energy is converted into another form of energy: for example, thermal energy, energy of deformation etc.). Suppose a mass m1 is moving with an initial velocity vi and collides with a mass m2, which is initially at rest (see Figure 2). The two masses stick together. What is the final velocity of the system, and what is the change in the kinetic energy of the system ?
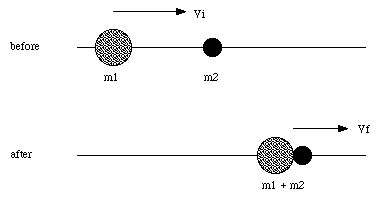
Figure 2. Completely Inelastic Collision.
The initial momentum of the system is
pi = m1 vi
The final momentum of the system is
pf = (m1 + m2) vf
Conservation of linear momentum implies
m1 vi = (m1 + m2) vf
or
![]()
The final velocity of the combined system will always be less than that of the incoming object.
© Frank L. H. Wolfs, University of Rochester, Rochester, NY 14627, USA
Last updated on Wednesday, March 14, 2001 10:43