Using a Motion Sensor
January 16, 21, & 23, 2002

Alice Tran

Lia Field


Abstract:
Motion is observable through many different facets. One facet is a motion sensor, in which the one-dimensional motion of an object can effectively be measured.

Theory:
Depending upon the variables of an experiment, different results occur under different conditions. Using the motion sensor, and viewing the data through a graph, one can view the motion of an object. The motion sensor uses pulses that reflect from an object back to the motion sensor, and determines the distance by the relative time difference between the emission of a pulse, and it’s reflection. With analysis, the data will show the starting point, displacement, velocity, and acceleration of an object during an experiment. Graphs are very important in the analysis of the experiment, as well as the reproduction of the motion.

Experimental:
1. The first task of the experiment was to set up the equipment. A support rod was secured to a base, and the motion sensor was placed on the rod at varying lengths depending upon the distance of the object. (If the object were close by, then the motion sensor would be placed only a few inches from the table, however, if it were a farther distance, the motion sensor should be place at the very top of the rod, to avoid interference from the table or other surrounding objects. And if we predicted the object to extremely far away, then we placed the base and rod on a chair, and the motion sensor on the top of the rod to measure this far away distance. If after a certain point there was interference from the floor, then we concluded that we could not measure any further, since we limited by our environment.) In addition, the motion sensor can be turned on by pressing REC in the control window, and it will automatically turn off after ten seconds. .

2. The second task of the experiment was to calibrate the motion sensor (which was a Pasco sonic motion sensor). This task was accomplished by taking a ruler and measuring the distance perpendicular to the front of the motion sensor. After measuring a certain distance, for example .5 meters (m), we placed a flat object at the .5 m mark, and turned on the motion sensor. If the motion sensor also measured .5 m, then we knew it was calibrated. Of course we repeated this several times at different lengths to reaffirm that the motion sensor was calibrated. Once the relative accuracy of the motion sensor was known, we tried to determine the minimum and maximum ranges of the motion sensor at different frequencies (120, 60, and 5 hertz).

3. In addition, we tried to reproduce the motion of and object in a given graph. After first analyzing the graph, and determining approximately where the object started, we tried moving the object back at a similar velocity as the graph, and then stopping at the moment the graph plateaued. After several tries, the given graph was somewhat (although not perfectly) reproducible.

4. From the data, we were able to draw some conclusion about the motion sensor, the different results obtained from different variables within the experiment (such as runs at different frequencies), the effects of velocity, and acceleration on the data.

Data Analysis:
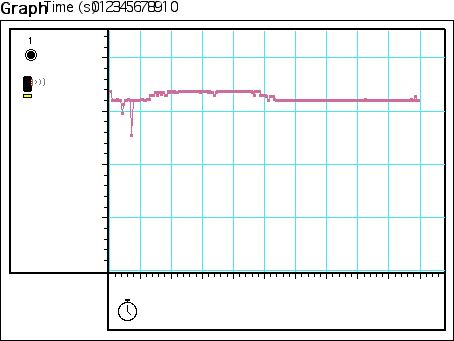
1. Data receive from the sensor could be observed through either looking at a time/position graph, or the digital meter. For the initial testing of the Motions Sensor (P00), the minimum reading possible was .4m (figure 1). This was determined after several tests of various measurements lower than .4m. The results of these tests would be much higher that what it should be (i.e. at .2 m, the senor would read .41m). The maximum was determined by seeing how far the sensor could read a distance before it was limited by the environment, or it started producing unexplainable readings. The maximum of P00 was 3.27m (figure 2). Note: that we were limited is several ways to determine the actual maximum range. First of all, we were limited by the environment, because even if the motion sensor had the ability to detect ranges farther than 3.27m, we could not measure it because, 3.27m was the boundary of the experiment setup (a black box at the other end of the table). In addition, since the sensor operates by sending sound in a cone, there is a slight discrepancy about the maximum range. The computer is technically only 3.14maway from the black box. However, since the motion sensor emits sound in a cone shape, the distance measure could have been the hypotenuse distance. This hypothesis is supported by the fact that according to Pythagorean’s theorem (a2+b2=c2), the hypotenuse distance would be 3.21m, which is close to the 3.27 meter indicated by the computer (diagram 1).

Figure 1
Figure 2


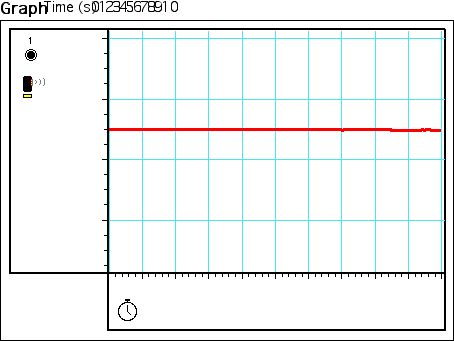
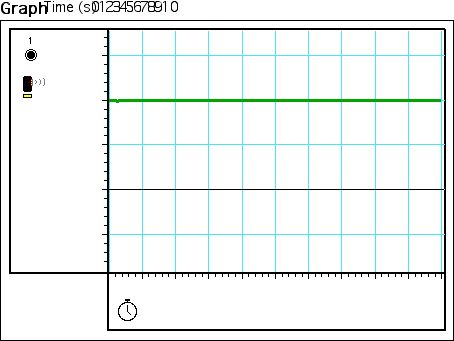
Both figures 3, and 4 show that motion sensor was calibrated, because at the measure of .5m, the sensor read .5m (figure 3), and at the measure of 1m, the sensor read 1m (figure 4).

 
Figure 3
Figure 4


Errors that might have occurred during experiment P00, (other that the measurement of the hypotenuse), included limitations of the experiment’s environment. These limitations include surrounding objects such as the computer, the back box, or other things like chairs, etc. A frequent limitation was the table. Since the sensor emitted sound as a cone, the cone often hit the table, and reflected back, before it hit the intended object. This problem could often be solved by raising the sensor higher, however the rod was only so tall, thus after a certain distance the sensor would eventually be hitting the table.


2. The experiments P00a, b, and c tested for the minimum and maximum ranges at different frequencies. P00a at 120 hertz, P00b at 60 hertz, and P00c at 5 Hertz.

Frequency (Hz)
Minimum Distance (m)
Maximum Distance (m)
120
.4
.6
60
.4
.85
5
.4
4.25*

* The true maximum of the sensor at 5 hertz could not be determine due to the limitations of the environment. Interference from the table, caused the readings to plateau. When we tried to adjust for this interference, by placing the rod and senor on a chair, (creating more distance between the senor and the floor) the sensor again plateaued but at a higher reading (4.25m). These tests shows that the when the distance between the sensor and wither the table or the floor increase, then the plateau increases. Thus the maximum measure possible is whatever the environment permits. In this case the maximum is therefore 4.25m.

** Note, that P00a did not work due to possible equipment defect. (Actual reason never determined, but after using a new motion sensor, results turned out normally.)

Due to the fact that that the motion sensors can’t distinguish between the burst it sends out, if the object is to far away, than a reflection of burst one, may be read as a reflection of burst 2, thus the object seems closer that it is in reality. Notice the spikes in most figures 5-13 (excluding calibration graphs). Thus the maximum distance a motion sensor can read is the distance at the first spike in the graph. It might have read an object further, away, but we can accurately determine if did because of the delay in reflection. Thus we determine that the 1st spike should be the indicator of the maximum distance.

In P00a, we determined the minimum by slowly moving an object farther away from the motion sensor, and analyzing the date output. We noticed that at points before .4m, the output were high, and consistent, then at .4m, it starting increasing. After several tests with the same results, we concluded that the minimum for 120hz was .4m (figure 5). The same method was use for finding the maximum. By moving an object slowly farther from the motion sensor, we looked at the data and observed any aberrations. We noticed that consistently, the slope of the graph increased after .4m, and sharply dropped at .6m (figure 6), even if the movement was a constant increase in distance. After several runs with the same results, we concluded that the maximum distance was .6m at 120hz. Figure 7 shows that the motion sensor in P00a was calibrated when the measurement was .6m, and the result was .61m (the difference could have been cause by human error).

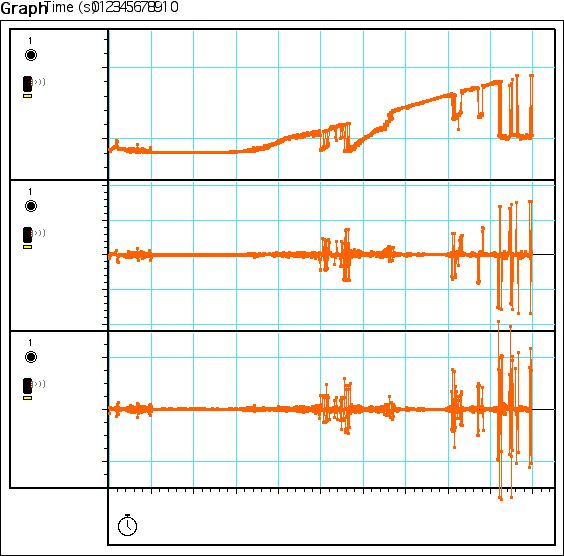Figure 5

Figure 6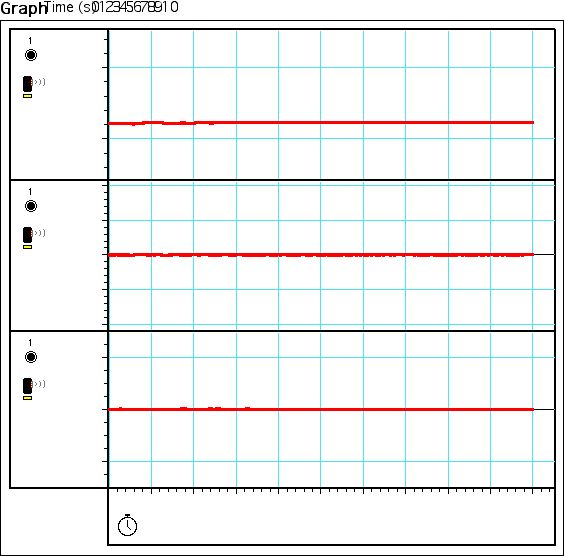

Figure 7

We used a similar procedure in P00b as in P00a, and found that the minimum was .4m (figure8) and the maximum was .85m (figure9), calibration at .6m equaled .6m (figure 10) at 60hz.

Figure 8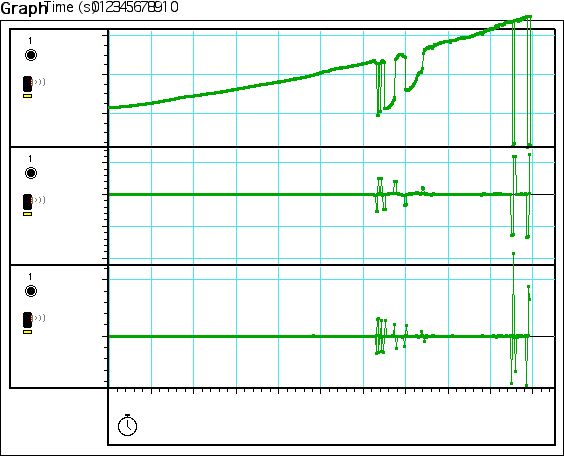


Figure 9

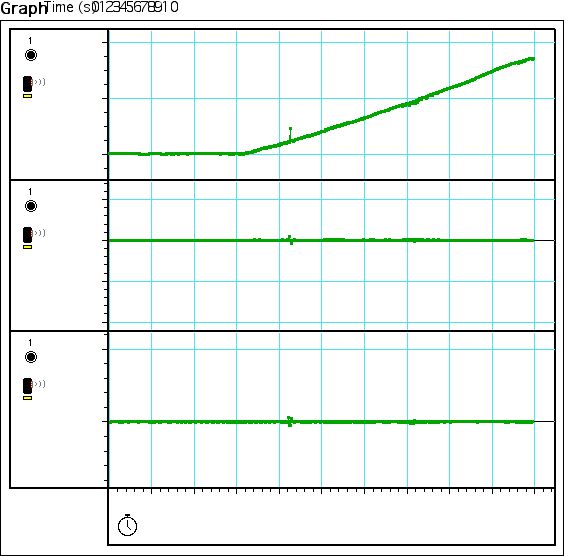
Figure 10

In experiment P00c, we also used a similar procedure to P00a and P00b. In determining the minimum we discovered that a points before .4m the results would increase to about .61, and then sharply decrease to .4m when at the measurement .4m. Thus we determined that this was the minimum point of the motion sensor at 5hz (figure 11). Starting at the minimum (.4m) we increased the distance, to determine the maximum distance. However we discovered that after a certain point the graph would plateau. We determined that this resulted in the interference from the table. So we attempted to compensate by raising the motion senor the maximum point on the rod, and then later by putting it on a chair (thus increasing the distance between the floor and the motion sensor) to determine the maximum distance. However even after these adjustments, we could only measure up to 4.25m (figure 12). This point was the maximum plateau. Although the sensor could have detected a larger distance, we were inhibited by the environment, thus to the best of our knowledge, the maximum at 5hz is 4.25m. The calibration for P00c is seen in figure 13, when a measurement of .5m resulted in an output of .5m.

Figure 11


Figure 12

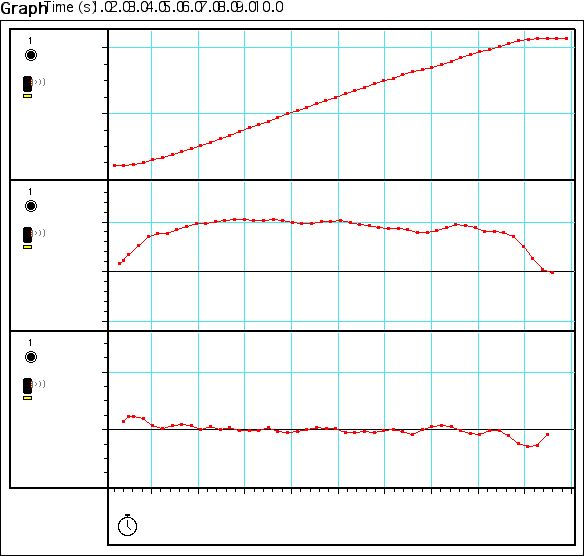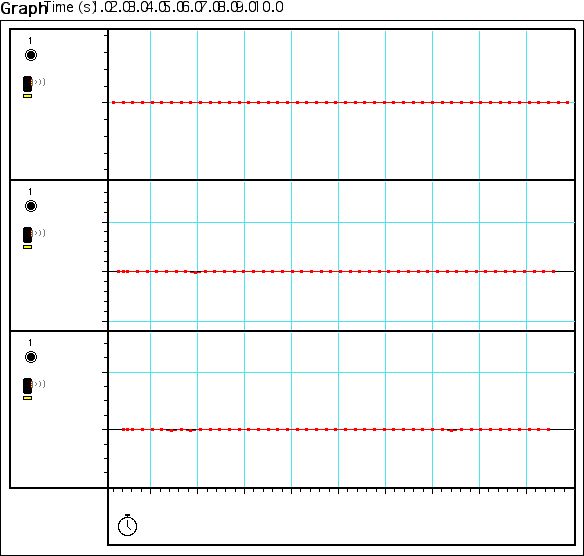Figure 13

Errors that might have occurred during P00a, b, and c, included the limitations of the experiment’s environment. These limitations included surrounding objects. The most common hindrance was the table. Since the sensor emitted sound as a cone, the cone often hit the table, and reflected back, before it hit the intended object. This problem could often be solved by raising the sensor higher, however the rod was only so tall, thus after a certain distance the sensor would eventually be hitting the table. In an attempt to determine a farther distance, we tried putting the base/rod on the chair, creating a taller effect, however eventually the cone hit the floor, and we had run out of solutions. Thus even if the motion sensor could read a longer distance, we could not prove this distance, due to the limitation of our environment. Conversely, if the sensor was too high, and the object too small, the cone could have missed the object completely (although we usually accounted for this, and thus had no data with this type of error).


3. In experiment P001 attempted to duplicate and experiment by tracing over the initial experiment’s graph. First we analyze the graph, and determined the starting point to be .4m. It is plateau at .4m, which indicated that the object is stationary. Then the distance increased at a certain velocity, and again plateaus at around 2.7m. With this information and the use of trail and error, we were able to reproduce the experiment with close degree of accuracy. In figure 14, the graph appears to quite similar to the original graph, with a chi-square of .085342. However we were able to improve the chi-square in figure 15 to .060071. The difference between the two graphs is very interesting because although figure 14 looks better than figure 15, figure 15 has more accurate points, and thus is a better reproduction of the experiment. Thus proving that looks can be deceiving, and analysis of a graph can’t a superficial glance at a graph, but also a more in depth look at the data.

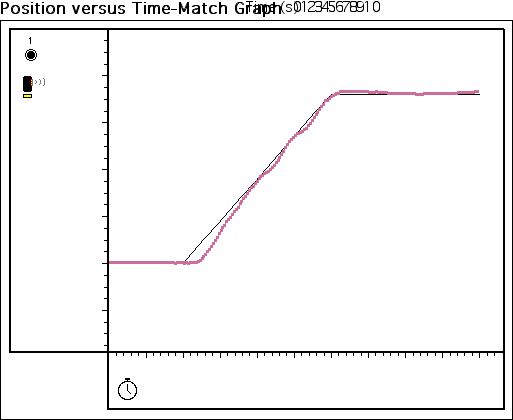Figure 14


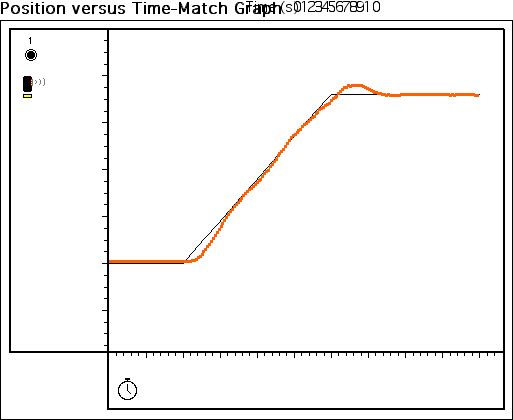Figure 15

Conclusions:
This experiment showed that at different frequencies, the range of measurement different. Hence the lower the frequency the longer the distance that could be measure, because the difference between burst was longer. Also, the motion sensor experiment has showed that one can’t take the data result at face value. One must not only analyze the graphs, but also determine what they mean. A graph may seem to show the distance of an object, however in reality, a slight aberration that could easily be over looked, may have important meaning. Although a graph may continue to increase as the object increases after a spike, this does not mean that it is a correct distance. A spike is an indication that the object is out of range, that the first burst is being reflected back after the second had been emitted, creating faulty data if interpreted wrongly. Thus once a spike occurs, we determined that at this point is the maximum distance the motions sensor can measure. In addition, when the graphs each experiment we look into closely, we noticed that there were several small aberrations, even though the digital meter may have output a consistent number. This shows that the graph may seem accurate; there may be slight discrepancies. However for the most part, the motion sensor measures distance within acceptable parameters.

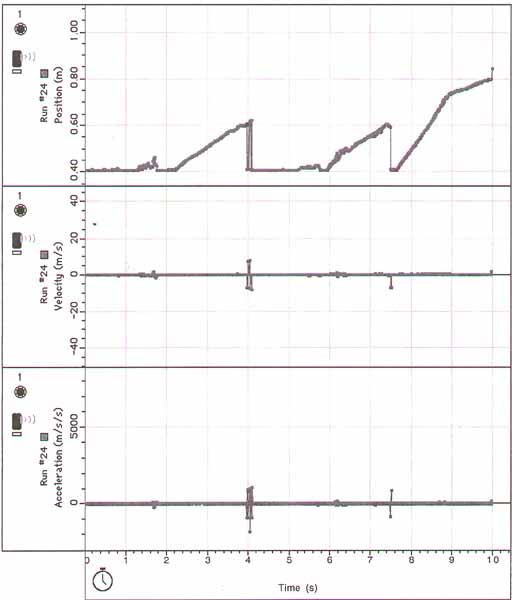
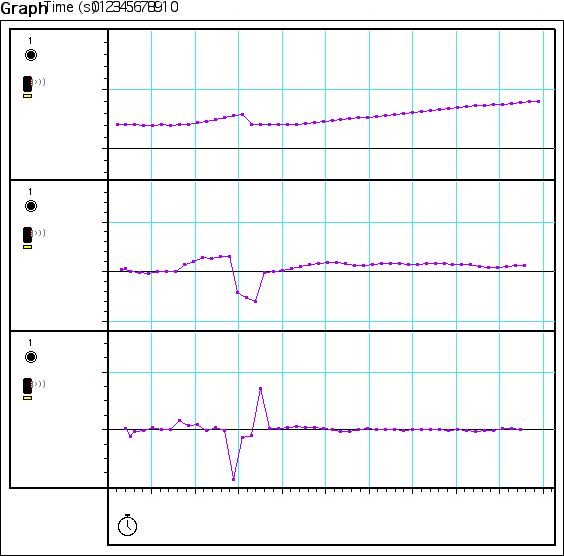
Also, after observing the velocity and acceleration graph while moving an object, I noticed that velocity was positive, when the object moved further away, and was negative when there was a decrease in distance. In addition, the acceleration was positive when the velocity increase, but was negative when it decreased.

Finally, errors occurred usually due to physical limitations, such as surround object interfering with reading the moving object, and the limited range caused by lack of height. Other errors included measuring the horizontal distance, when the sensor when the hypotenuse distance, and simple human error. However for the most part, this lab went smoothly as predicted.


Remarks:
This experiment was very useful in showing that error often occurs, and that one must closely analyze the data before coming to a conclusion. And although we never were able to determine why the experiment didn’t work the second day of class, I was thankful, that the experiment began to go well the follow lab.