Superconductivity
Purpose:
To observe the levitation of the magnet due to the Meisner Effect,
calculate the critical temperature of a superconducting material by direct
observations of the levitation and by measuring the resistance of the superconducting material as a function
of temperature.
Introduction
The flow of current in normal conductors dissipates energy (producing
heat). This "frictional" dissipation is measured by the resistivity of the
material and is the origin of Ohm's Law.
At lower temperatures some materials called superconductors lose measurable
electrical resistivity. Without any driving voltage, superconducting currents
will flow indefinitely with no discernible decay. This phenomenon was
originally discovered in 1911 by the Dutch physicist Heike Kamerlingh-Onnes
(Nobel Prize: 1913) as a byproduct of his ability to liquefy Helium.
The superconducting transition occurs over a relatively small change in
temperature. The temperature at which it occurs, which is called the critical
temperature
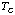 ,
depends on the material. Until recently the known superconductors had a
,
depends on the material. Until recently the known superconductors had a
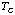 below 23K. The new (Nobel Prize: 1987) ceramic superconductors used in this
experiment have much higher critical temperatures (around 90K) and have less
abrupt transitions than those of the original metallic superconductors. Since
easily available liquid nitrogen boils at 77K these materials make
superconducting phenomenon observable above 77K.
below 23K. The new (Nobel Prize: 1987) ceramic superconductors used in this
experiment have much higher critical temperatures (around 90K) and have less
abrupt transitions than those of the original metallic superconductors. Since
easily available liquid nitrogen boils at 77K these materials make
superconducting phenomenon observable above 77K.
The theoretical understanding of the phenomena of superconductivity in these
materials is not entirely understood. Before the discovery of the ceramic
superconductors in 1986, the accepted model was the BCS theory (Bardeen, Cooper
and Schrieffer). According to this theory a superconducting current is carried
by bound pairs of electrons (Cooper pairs) which move through a metal without
energy dissipation. The mechanism for the new ceramic superconductors remains
unknown and is the subject of present day research.
Another striking feature of superconductors is that they are perfectly
diamagnetic. When superconducting, a superconductor will not allow any
magnetic field to penetrate it. The presence of an external magnetic field
that would penetrate an ordinary conductor produces a "supercurrent" on the
surface of a superconductor which generates a magnetic field that precisely
cancels the external field in the interior of the superconductor. This induced
field, opposing the external field, repels it. A magnet, for instance,
producing such an external field will be repelled. Therefore, this magnetic
repulsion phenomenon is called the Meissner Effect named after the
person who discovered it in 1933. It is a unique signature of
superconductors.
The purpose of this laboratory is to introduce students to superconductivity
and demonstrate the characteristic properties of superconductors. By use of
the ceramic high temperature superconductors provided, you will observe the
Meissner effect in which a magnetic field is excluded from the interior of a
superconductor. Also you will observe that the electrical resistance vanishes
when the material becomes superconducting, and you will measure the critical
temperature and determine the Resistance vs. Temperature characteristic.
In the process you will learn the principle (based on Ohm's law) of the use of
a four point probe to measure the resistance of a material (in spite of the
interfering effects of contact resistance) by making voltage and current
measurements.
Prelab Homework
This prelab homework must be done at home and handed to the lab TA
before you start the lab. Students should read the instructions for this lab,
and consult the sections on Electricity and Magnetism in your textbook in order
to answer the questions below.
Questions
- State the expression for Ohm's law. If a voltage of 10 Volts is
placed across a 3 Ohm resistor, what is the current through the
resistor?
- What is the critical temperature for a superconducting material?
- What voltage given by the thermocouple in the experiment
corresponds to the temperature of liquid nitrogen? (Use the table in the appendix).
- The critical temperature of your sample lies
between 77K and 90K. What is the corresponding range of thermocouple voltages ?
- Suppose your thermocouple has a systematic error:
at 77K it gives 6.12 mV. What temperature of the sample corresponds to 5.63 mV?
The Experiment: Part I
A: The Meissner Effect. Levitation of the Magnet.
With a strong enough magnet, the repulsion due to the Meissner effect can be
sufficient to support the weight of the magnet. Such a magnet will levitate
above a superconductor.
Precautions
In this experiment you will handle liquid nitrogen which can cause
severe "burns" because of its extremely low temperature. Certain precautions
need to be taken. You should read the following instructions carefully and
practice these safety measures in the experiment.
- Wear safety glasses at all times in the presence of liquid nitrogen. Do not
allow any liquid nitrogen to touch your body, and do not touch anything that
has been immersed in it until that item warms to room temperature.
- Be extremely careful not to overfill or to spill liquid nitrogen from any
vessel. Never store liquid nitrogen in a container with a tight-fitting lid
because over pressure by the evaporated nitrogen may cause an explosion.
- The superconductors are made of metal oxides that may be potentially toxic.
For your safety, never handle the superconductor with your bare hands. Use the
tweezers provided. Wash your hands with soap and water after the experiment is
completed.
Procedure for Part IA:
- Carefully pour a small amount of liquid nitrogen in the
cylindrical section of styrofoam tray. Wait until it stops boiling.
- Using the plastic tweezers provided, place the superconductor disk
flat in the liquid. Wait until it stops boiling. The liquid should be level
with the top of the disk.
- Using the tweezers pick up one of the magnets provided and place it
on top of the superconductor disk. Observe whether the magnet is touching the
surface of the disk.
- Record your qualitative observations of this phenomena.
B: Meisner Effect. The Critical Temperature of the Superconductor.
You can determine 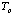 by observing the Meissner effect. Above the critical temperature a material
will be in a normal state and will no longer expel magnetic field. By
measuring the temperature at which the Meissner effect disappears as the
superconductor is warming up you can determine the
by observing the Meissner effect. Above the critical temperature a material
will be in a normal state and will no longer expel magnetic field. By
measuring the temperature at which the Meissner effect disappears as the
superconductor is warming up you can determine the
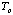 .
.
The temperature of the superconductor will be determined with a thermocouple
attached to the superconductor. Figure 9.1 the actual device and gives the
color code of the six leads. At this stage only the thermocouple leads (blue
and red) will be used.
The thermocouple junction thermometer consists of two different metals
connected at a point to form a junction. This kind of bi-metallic junction
produces a small electrical voltage which varies with the temperature of the
thermocouple junction. The voltage to temperature conversion is given in Table
9.1.
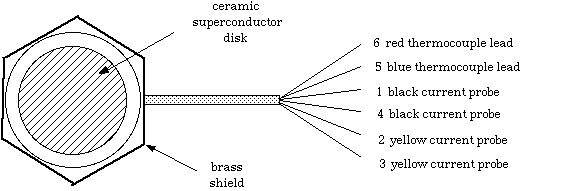
Figure 9.1
Procedure for Part IB:
- Connect the thermocouple leads to the voltmeter provided.
- Select the right range to read to an accuracy of 0.01 mV.
- Immerse the superconducting device completely in liquid nitrogen.
Wait until the boiling stops. The voltmeter should read 6.43 mV corresponding
to the liquid nitrogen temperature of 77K. If your voltmeter reads a different
value then there is an error which may be due to contact potentials or changes
in the thermocouple. You can assume that when immersed in liquid nitrogen that
the temperature of the thermocouple is 77K. For example if the thermocouple
reads 6.23 mV, then you must add 0.20 mV to all readings to determine the
temperature in all later measurements.
- Remove the device from the liquid nitrogen and place it flat on an
insulating surface with the superconductor's surface exposed. The
superconducting material will start to warm up from 77K.
- Carefully place the magnet provided on top of the superconductor so
that it "floats" over the center of the disk via the Meissner Effect.
- When the magnet drops onto the surface of the superconductor disk,
record the voltmeter reading of the thermocouple. The corresponding
temperature from the table is the superconducting transition temperature
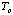 .
The expected transition temperature is about 90K or less for some of the
samples. You will see from the table that this is a change of about 0.5 mV. The
magnets will drop after about 40 to 120s depending on your apparatus.
.
The expected transition temperature is about 90K or less for some of the
samples. You will see from the table that this is a change of about 0.5 mV. The
magnets will drop after about 40 to 120s depending on your apparatus.
- Repeat procedure one more time.
The Experiment: Part II
Resistance vs Temperature.
You will measure the resistance of the superconductor device as a
function of temperature to determine
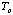 .
You will use the thermocouple to measure the temperature, as above, and use a
four point probe to measure the resistance.
.
You will use the thermocouple to measure the temperature, as above, and use a
four point probe to measure the resistance.
When a simple measurement of the resistance of an electrical test sample is
performed by attaching two wires to it, the resistance of the wire-to-sample
contact point or bond is also inadvertently included. If the sample resistance
is very small, the contact resistance can dominate and completely obscure the
temperature dependence of the sample resistance. The solution to this problem
is to use the four point probe shown schematically in the Figure 9.2. A
constant current
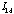 (~ 0.5 A)
is made to flow the length of the sample through two probes labeled 1 and 4.
If the sample has any resistance to the flow of the electrical current, there
will be a voltage drop
(~ 0.5 A)
is made to flow the length of the sample through two probes labeled 1 and 4.
If the sample has any resistance to the flow of the electrical current, there
will be a voltage drop
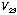 between the two center probes labeled 2 and 3. The voltage drop between probes
2 and 3 can be measured by a voltmeter. The high input impedance of the
voltmeter minimizes the current flow through it. Then the potential drop
across the contact resistance associated with probes 2 and 3 is negligible.
Therefore, the resistance of the sample between probes 2 and 3 is the ratio of
the voltage drop
between the two center probes labeled 2 and 3. The voltage drop between probes
2 and 3 can be measured by a voltmeter. The high input impedance of the
voltmeter minimizes the current flow through it. Then the potential drop
across the contact resistance associated with probes 2 and 3 is negligible.
Therefore, the resistance of the sample between probes 2 and 3 is the ratio of
the voltage drop
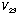 to the current
to the current
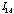 ,
,
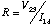 . (9.1)
. (9.1)
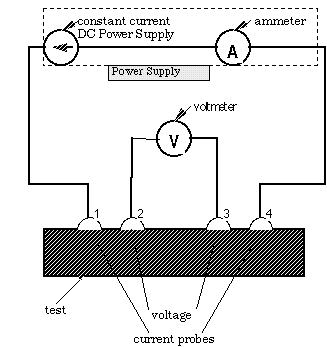
Figure 9.2. Schematic of a Four Point Probe
Procedure for Part II.
Data Analysis
- Plot
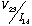 vs. temperature.
vs. temperature.
- Discuss the
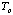 determined both by measuring the resistance and by observing the Meissner
Effect. Is there any difference? Why?
determined both by measuring the resistance and by observing the Meissner
Effect. Is there any difference? Why?
Questions
- The Meissner Effect allows a magnet to float above a superconductor
(or vice versa). Can you think of any potential applications using this
effect?
References
Ashcroft and Mermin, Solid State Physics. New York: pp.
726-755
Tinkham, Superconductivity. New York:
Prochnow, David. Superconductivity, Experimenting in a New
Technology. Blue Ridge Summit, PA: TAB Books Inc., 1989.
Kinzie, P. A. Thermocouple Temperature Measurement. NY: Wiley-Interscience,
1973.
Table for converting Voltage given by thermocouple (mV) to Temperature (K)
0K 0 1 2 3 4 5 6 7 8 9 10 deg.K
60 7.60 7.53 7.46 7.40 7.33 7.26 7.19 7.12 7.05 6.99 6.92 60
70 6.92 6.85 6.78 6.71 6.64 6.56 6.49 6.42 6.37 6.33 6.29 70
80 6.29 6.25 6.21 6.17 6.13 6.09 6.05 6.01 5.97 5.93 5.90 80
90 5.90 5.86 5.83 5.79 5.75 5.72 5.68 5.64 5.60 5.56 5.52 90
100 5.52 5.48 5.44 5.41 5.37 5.34 5.30 5.27 5.23 5.20 5.16 100
110 5.16 5.13 5.09 5.06 5.02 4.99 4.95 4.91 4.88 4.84 4.81 110
120 4.81 4.77 4.74 4.70 4.67 4.63 4.60 4.56 4.53 4.49 4.46 120
130 4.46 4.42 4.39 4.35 4.32 4.28 4.25 4.21 4.18 4.14 4.11 130
140 4.11 4.07 4.04 4.00 3.97 3.93 3.90 3.86 3.83 3.79 3.76 140
150 3.76 3.73 3.69 3.66 3.63 3.60 3.56 3.53 3.50 3.47 3.43 150
160 3.43 3.40 3.37 3.34 3.30 3.27 3.24 3.21 3.18 3.15 3.12 160
170 3.12 3.09 3.06 3.03 3.00 2.97 2.94 2.91 2.88 2.85 2.82 170
180 2.82 2.79 2.76 2.73 2.70 2.67 2.64 2.61 2.58 2.53 2.52 180
190 2.52 2.49 2.46 2.43 2.40 2.37 2.34 2.31 2.29 2.26 2.23 190
200 2.23 2.20 2.17 2.14 2.11 2.08 2.05 2.02 1.99 1.96 1.93 200
210 1.93 1.90 1.87 1.84 1.81 1.78 1.75 1.72 1.69 1.66 1.64 210
220 1.64 1.61 1.59 1.56 1.54 1.51 1.49 1.46 1.44 1.41 1.39 220
230 1.39 1.36 1.34 1.31 1.29 1.26 1.24 1.21 1.19 1.16 1.14 230
240 1.14 1.11 1.09 1.07 1.04 1.02 0.99 0.97 0.94 0.92 0.89 240
250 0.89 0.87 0.84 0.82 0.79 0.77 0.74 0.72 0.69 0.67 0.65 250
260 0.65 0.62 0.60 0.58 0.55 0.53 0.50 0.48 0.45 0.42 0.40 260
270 0.40 0.38 0.36 0.34 0.32 0.30 0.28 0.26 0.24 0.22 0.20 270
280 0.20 0.18 0.16 0.14 0.12 0.10 0.08 0.06 0.04 0.02 0.00 280
290 0.00 -.02 -.04 -.06 -.08 -.10 -.12 -.14 -.16 -.18 -.20 290
300 -.20 -.22 -.24 -.26 -.28 -.30 -.32 -.34 -.36 -.38 -.40 300
deg.K 0 1 2 3 4 5 6 7 8 9 10 deg.K
Table 9.1. Conversion from mV to K for the thermocouple
Send comments, questions and/or suggestions via email to wolfs@nsrl.rochester.edu.
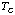 ,
depends on the material. Until recently the known superconductors had a
,
depends on the material. Until recently the known superconductors had a
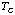 below 23K. The new (Nobel Prize: 1987) ceramic superconductors used in this
experiment have much higher critical temperatures (around 90K) and have less
abrupt transitions than those of the original metallic superconductors. Since
easily available liquid nitrogen boils at 77K these materials make
superconducting phenomenon observable above 77K.
below 23K. The new (Nobel Prize: 1987) ceramic superconductors used in this
experiment have much higher critical temperatures (around 90K) and have less
abrupt transitions than those of the original metallic superconductors. Since
easily available liquid nitrogen boils at 77K these materials make
superconducting phenomenon observable above 77K. 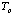 by observing the Meissner effect. Above the critical temperature a material
will be in a normal state and will no longer expel magnetic field. By
measuring the temperature at which the Meissner effect disappears as the
superconductor is warming up you can determine the
by observing the Meissner effect. Above the critical temperature a material
will be in a normal state and will no longer expel magnetic field. By
measuring the temperature at which the Meissner effect disappears as the
superconductor is warming up you can determine the
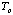 .
.
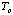 .
The expected transition temperature is about 90K or less for some of the
samples. You will see from the table that this is a change of about 0.5 mV. The
magnets will drop after about 40 to 120s depending on your apparatus.
.
The expected transition temperature is about 90K or less for some of the
samples. You will see from the table that this is a change of about 0.5 mV. The
magnets will drop after about 40 to 120s depending on your apparatus. 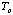 .
You will use the thermocouple to measure the temperature, as above, and use a
four point probe to measure the resistance.
.
You will use the thermocouple to measure the temperature, as above, and use a
four point probe to measure the resistance.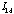 (~ 0.5 A)
is made to flow the length of the sample through two probes labeled 1 and 4.
If the sample has any resistance to the flow of the electrical current, there
will be a voltage drop
(~ 0.5 A)
is made to flow the length of the sample through two probes labeled 1 and 4.
If the sample has any resistance to the flow of the electrical current, there
will be a voltage drop
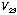 between the two center probes labeled 2 and 3. The voltage drop between probes
2 and 3 can be measured by a voltmeter. The high input impedance of the
voltmeter minimizes the current flow through it. Then the potential drop
across the contact resistance associated with probes 2 and 3 is negligible.
Therefore, the resistance of the sample between probes 2 and 3 is the ratio of
the voltage drop
between the two center probes labeled 2 and 3. The voltage drop between probes
2 and 3 can be measured by a voltmeter. The high input impedance of the
voltmeter minimizes the current flow through it. Then the potential drop
across the contact resistance associated with probes 2 and 3 is negligible.
Therefore, the resistance of the sample between probes 2 and 3 is the ratio of
the voltage drop
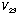 to the current
to the current
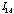 ,
,
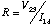 . (9.1)
. (9.1)
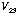 .
The voltage of the thermocouple will be measured with another voltmeter which
is supplied.
.
The voltage of the thermocouple will be measured with another voltmeter which
is supplied.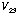 ,
your voltmeter will show a small voltage.
,
your voltmeter will show a small voltage. 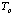 .
.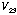 vs. temperature measurements.
vs. temperature measurements.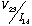 vs. temperature.
vs. temperature.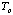 determined both by measuring the resistance and by observing the Meissner
Effect. Is there any difference? Why?
determined both by measuring the resistance and by observing the Meissner
Effect. Is there any difference? Why?