NOTE
This manual describes the laboratory experiment used during the 1996 - 1997 academic year. Significant changes have been made since then, and the manual used during the current academic year is in NOT available yet on the WEB. Hardcopies can be purchased at the bookstore.
To observe two of the fudamental properties of superconductors. The first is the levitation of a magnet by a superconductor which illustates the Meisner Effect. Secondly, direct measurement of the resistance of the superconducting material as a function of temperature reveals the zero resistance state below a certain temperature. (Hence the name superconductor).
The flow of current in normal conductors dissipates energy (producing heat). This "frictional" dissipation is measured by the resistivity of the material and is the origin of Ohm's Law.
At lower temperatures some materials called superconductors lose measurable electrical resistivity. Without any driving voltage, superconducting currents will flow indefinitely with no discernible decay. This phenomenon was originally discovered in 1911 by the Dutch physicist Heike Kamerlingh-Onnes (Nobel Prize: 1913) ..
The superconducting transition occurs over a relatively small
change in temperature. The temperature at which it occurs, which
is called the critical temperature 
,
depends on the material. Until recently, the known superconductors
had a 
below 23K. The new ceramic
superconductors (Nobel Prize: 1987) used in this experiment have
much higher critical temperatures ( 90-100K) than those of the
original metallic superconductors. Since easily available liquid
nitrogen boils at 77K ,these materials make superconducting phenomenon
easily observable above 77K.
The theoretical understanding of the phenomena of superconductivity in these materials is not entirely understood. Before the discovery of the ceramic superconductors in 1986, the accepted model was the BCS theory (Bardeen, Cooper and Schrieffer. Noble Prize 1957). According to this theory a superconducting current is carried by bound pairs of electrons (Cooper pairs) which move through a metal without energy dissipation. The mechanism for the new ceramic superconductors remains unknown and is the subject of present day research.
Another striking property of superconductors is that they are perfectly diamagnetic.
When superconducting, a superconductor will not allow any magnetic field to penetrate it. This is the Meisner Effect!( named after the person who discovered this effect in 1933). Any external magnetic field which would penetrate the superconducting material is cancelled by an opposing field produced by electric currents induced in the superconductor. If this external field comes from a magnet, then the expulsion results in a repulsive force on the magnet The magnet, if above the superconductor ,will be levitated. This magnetic repulsion phenomenon is a manifistation of the the Meissner Effect .
The purpose of this laboratory is to introduce students to superconductivity and demonstrate the characteristic properties of superconductors. With the use of the ceramic high temperature superconductors provided, you will observe the Meissner effect in which a magnetic field is excluded from the interior of a superconductor. Also you will observe that the electrical resistance vanishes when the material becomes superconducting, and you will measure the critical temperature and determine the Resistance vs. Temperature characteristic. In the process you will learn the principle (based on Ohm's law) of the use of a four point probe to measure the resistance of a material (in spite of the interfering effects of contact resistance) by making voltage and current measurements.
This prelab homework must be done at home and handed to the lab TA before you start the lab. Students should read the instructions for this lab, and consult the sections on Electricity and Magnetism in your textbook in order to answer the questions below.
1) State the expression for Ohm's law. If a voltage of 10 Volts is placed across a 3 Ohm resistor, what is the current through the resistor?
2) State the expression for Hook's law. If superconductor has a weigh of 10 g and it levitated 5 cm. What is constant of superconductor if it was on normal earth atmosphere ?
3) What is the critical temperature for a superconducting material?
4) a. What voltage given by the thermocouple in the experiment corresponds to the temperature of liquid nitrogen? (Use the table in the appendix).
b. The critical temperature of your sample lies between 77K and 90K. What is the corresponding range of thermocouple voltages ?
c. Suppose your thermocouple has a systematic error: at 77K it gives 6.12mV. What temperature of the sample corresponds to 5.63 mV?
5) What is the purpose of using the sand crystals?
With a strong enough magnet, the repulsion due to the Meissner effect can be sufficient to support the weight of the magnet. Such a magnet will levitate above a superconductor.
In this experiment you will handle liquid nitrogen which can cause severe "burns" because of its extremely low temperature. Certain precautions need to be taken. You should read the following instructions carefully and practice these safety measures in the experiment.
* Wear safety glasses at all times in the presence of liquid nitrogen. Do not allow any liquid nitrogen to touch your body, and do not touch anything that has been immersed in it until that item warms to room temperature. Keep it away from the water.
* Be extremely careful not to overfill or to spill liquid nitrogen from any vessel. Never store liquid nitrogen in a container with a tight-fitting lid because over pressure by the evaporated nitrogen may cause an explosion.
* The superconductors are made of metal oxides that may be potentially toxic. For your safety, never handle the superconductor with your bare hands. Use the tweezers provided. Wash your hands with soap and water after the experiment is completed.
(The components [Colorado Superconductor] for this part are listed in the end. Your TA will show them to you)
1) Carefully pour a small amount of liquid nitrogen in the cylindrical section of the styrofoam tray. Wait until it stops boiling.
2) Using the plastic tweezers provided, place the superconductor disk flat in the liquid. Wait until it stops boiling. The liquid should be level with the top of the disk.
3) Using the tweezers pick up one of the magnets provided and place it on top of the superconductor disk. Observe whether the magnet is touching the surface of the disk.
4) Record your observations of this phenomena.
(The components [Superconductive Components] for this part are listed in the end. Your TA will show them to you)
1) Place the superconducting levitator ring assembly in the Petri dish and slowly pour liquid N2 until the ring is completely cooled and the liquid N2 has settled to a slow boil.
2) Pick up the magnet ring and carefully move it toward the sample. One should feel a strong repulsive force as the magnet is moved towards the sample.
3) Stabilize the magnet [ push it down and release it] and give it a small spin. The magnet will keep rotating for some time, though it will slow down primarily because of air drag.
[The following steps 5-7 are optional for the fall 1996 term.]
4) Place the plastic plate on the magnet ring.
5) Add weigh on top of plastic plate (it already mark weigh , 10g, 20g, 50g, ...) and record weigh. Record levitate distance between magnet ring and levitator ring assembly.
6) Repeat step 5) until magnet ring falls down completely.
7) Plot the data , Force Vs distance.
You can determine 
by observing
the Meissner effect. Above the critical temperature a material
will be in a normal state and will no longer expel magnetic field.
By measuring the temperature at which the Meissner effect disappears
as the superconductor is warming up you can determine the
.
The temperature of the superconductor will be determined with a thermocouple attached to the superconductor. Figure 9.1 the actual device and gives the color code of the six leads. At this stage only the thermocouple leads (blue and red) will be used.
The thermocouple junction thermometer consists of two different metals connected at a point to form a junction. This kind of bi-metallic junction produces a small electrical voltage which varies with the temperature of the thermocouple junction. The voltage to temperature conversion is given in Table 9.1.
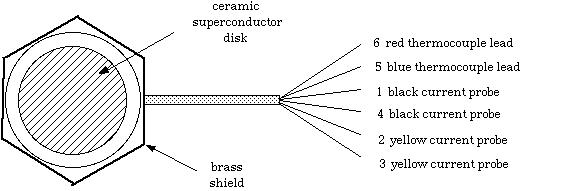
Figure 9.1
1) Connect the thermocouple leads to the voltmeter provided.
2) Select the right range to read to an accuracy of 0.01mV.
3) Cover the sample and holder with a plastic bag before immersing in liquid nitrogen. ( This will prevent moisture from condensing.) Wait until the boiling stops. The voltmeter should read 6.43mV corresponding to the liquid nitrogen temperature of 77K. If your voltmeter reads a different value then there is a systematic error which may be due to contact potentials associated with the thermocouple. If this is the case, you should assume that when immersed in liquid nitrogen that the temperature of the thermocouple is 77K. For example if the thermocouple voltage reads 6.23mV, then you must add 0.20mV to all readings to determine the temperature in all later measurements.
4) Remove the sample and holder from the liquid nitrogen and remove the plastic. Place it into the styofoam holder with the superconductor's surface exposed and close the cover. The superconducting material and holder will start to warm from 77K.
5) Open the cover and carefully place the provided magnet on top of the superconductor so that it "floats" over the center of the disk (via the Meissner Effect!).
6) When the magnet drops onto the surface of the superconductor
disk, record the voltmeter reading of the thermocouple. The corresponding
temperature from the table is the superconducting transition temperature
. The expected transition
temperature is about 110K( or somewhat less for some of the samples).
You will see from the table below that this is a change of about
1.23mV ( or less). The magnets will fall after about 40 to 120s
depending on your apparatus.
7) Repeat one more time.
You will measure the resistance of the superconductor device
as a function of temperature to determine 
.
You will use the thermocouple to measure the temperature, as above,
and use a four point probe to measure the resistance.
When a simple measurement of the resistance of an electrical
test sample is performed by attaching two wires to it, the resistance
of the wire-to-sample contact point or bond is also inadvertently
included. If the sample resistance is very small, the contact
resistance can dominate and completely obscure the temperature
dependence of the sample resistance. The solution to this problem
is to use the four point probe shown schematically in the Figure
9.2. A constant current 
(~0.25A)
is made to flow the length of the sample through two probes labeled
1 and 4. If the sample has any resistance to the flow of the electrical
current, there will be a voltage drop 
between the two center probes labeled 2 and 3. The voltage drop
between probes 2 and 3 can be measured by a voltmeter. The high
input impedance of the voltmeter minimizes the current flow through
it. Then the potential drop across the contact resistance associated
with probes 2 and 3 is negligible. Therefore, the resistance of
the sample between probes 2 and 3 is the ratio of the voltage
drop 
to the current
,
(9.1)
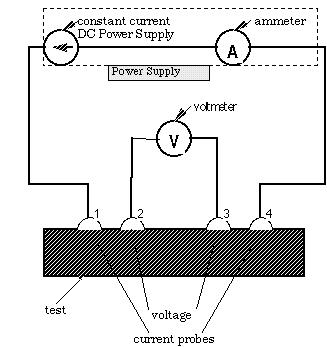
Figure 9.2. Schematic of a Four Point Probe
1) Set up equipment shown in fig 2 for the four point probe.
The color code of the leads is given in Figure 9.1. In this section
the voltmeter that you used to measure the voltage will now be
used to measure 
.
2) Put the superconductor and holder into the Crystat chamber (Plastice Cup) (see fig 9.3). Pour the sand into of cup until the superconductor is covered by sand ( Do not fill the entire cup). Carefully pour some liquid nitrogen into the cup and wait until the boiling stops. Continue to pour the liquid nitrogen until thermocouple reachs 6.43mV or comes to equilibrium near this value as discribed above.
3) Adjust the DC power supply to have a current of about 0.25A
through electrical lead and 4. Even though the resistance is supposed
to be zero and hence 
, your voltmeter
will show a small voltage. (Due to some resistance in the electrical
leads.)
Caution: Don't leave the current passing through the sample is above 200K for very long or it will cook and damage the sample.
4) Record simultaneously, the readings of the voltmeter connected to electrical leads 2 and 3 and of those connected to the thermocouple as the superconductor device warms up. This takes about 20 to 30 minutes. Try to take these readings as the thermocouple changes by 0.1mV increments and record the time . You may stop taking data when T has reached about 130K.
5) Repeat the 
vs. temperature
measurements.(Go back to step 2)
6) The ceramic superconductors are sensitive to moisture and will degrade in a humid environment. After completing the experiment, warm (don't cook it!) it carefully with hair dryer (at least 12 inches away!) for about 3 minutes (only!) to completely dry it.
Figure 9.3: Cross Section of the Sand Cryostat containing a CSI four-point probe device
1) Plot temperature and R (= V23 / I14) vs time.
2) Plot R (= V23 / I14) vs. temperature. From this plot indicate the transition temperature.
3) Discuss the 
determined
both from the above plot and by the observation the Meissner Effect.
Is there any difference? Why?
1) The Meissner Effect allows a magnet to float above a superconductor (or vice versa). Can you think of any potential applications using this effect?
1) Ashcroft and Mermin, Solid State Physics. New York: pp. 726-755
2) Prochnow, David. Superconductivity, Experimenting in a New Technology. Blue Ridge Summit, PA: TAB Books Inc., 1989.
3) Kinzie, P. A. Thermocouple Temperature Measurement. NY: Wiley-Interscience, 1973.
0K
0
1
2
3
4
5
6
7
8
9
10
deg.K
60
7.60
7.53
7.46
7.40
7.33
7.26
7.19
7.12
7.05
6.99
6.92
60
70
6.92
6.85
6.78
6.71
6.64
6.56
6.49
6.42
6.37
6.33
6.29
70
80
6.29
6.25
6.21
6.17
6.13
6.09
6.05
6.01
5.97
5.93
5.90
80
90
5.90
5.86
5.83
5.79
5.75
5.72
5.68
5.64
5.60
5.56
5.52
90
100
5.52
5.48
5.44
5.41
5.37
5.34
5.30
5.27
5.23
5.20
5.16
100
110
5.16
5.13
5.09
5.06
5.02
4.99
4.95
4.91
4.88
4.84
4.81
110
120
4.81
4.77
4.74
4.70
4.67
4.63
4.60
4.56
4.53
4.49
4.46
120
130
4.46
4.42
4.39
4.35
4.32
4.28
4.25
4.21
4.18
4.14
4.11
130
140
4.11
4.07
4.04
4.00
3.97
3.93
3.90
3.86
3.83
3.79
3.76
140
150
3.76
3.73
3.69
3.66
3.63
3.60
3.56
3.53
3.50
3.47
3.43
150
160
3.43
3.40
3.37
3.34
3.30
3.27
3.24
3.21
3.18
3.15
3.12
160
170
3.12
3.09
3.06
3.03
3.00
2.97
2.94
2.91
2.88
2.85
2.82
170
180
2.82
2.79
2.76
2.73
2.70
2.67
2.64
2.61
2.58
2.53
2.52
180
190
2.52
2.49
2.46
2.43
2.40
2.37
2.34
2.31
2.29
2.26
2.23
190
200
2.23
2.20
2.17
2.14
2.11
2.08
2.05
2.02
1.99
1.96
1.93
200
210
1.93
1.90
1.87
1.84
1.81
1.78
1.75
1.72
1.69
1.66
1.64
210
220
1.64
1.61
1.59
1.56
1.54
1.51
1.49
1.46
1.44
1.41
1.39
220
230
1.39
1.36
1.34
1.31
1.29
1.26
1.24
1.21
1.19
1.16
1.14
230
240
1.14
1.11
1.09
1.07
1.04
1.02
0.99
0.97
0.94
0.92
0.89
240
250
0.89
0.87
0.84
0.82
0.79
0.77
0.74
0.72
0.69
0.67
0.65
250
260
0.65
0.62
0.60
0.58
0.55
0.53
0.50
0.48
0.45
0.42
0.40
260
270
0.40
0.38
0.36
0.34
0.32
0.30
0.28
0.26
0.24
0.22
0.20
270
280
0.20
0.18
0.16
0.14
0.12
0.10
0.08
0.06
0.04
0.02
0.00
280
290
0.00
-0.02
-0.04
-0.06
-0.08
-0.10
-0.12
-0.14
-0.16
-.0.18
-0.20
290
300
-0.20
-0.22
-0.24
-0.26
-0.28
-0.30
-0.32
-0.34
-0.36
-0.38
-0.40
300
deg.K
0
1
2
3
4
5
6
7
8
9
10
deg.K
Conversion from mV to K for the thermocouple
Table 9.1