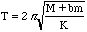 ,
(4.1)
,
(4.1)
Moment of Inertia and Oscillations
To measure the moment of inertia of three different objects about a specified rotational axis and to verify the parallel axis theorem.
The prelab homework must be done at home and handed to the lab TA before you start the lab. Read the instructions for this lab.
The period of oscillation of a mass M on a spring of mass m is,
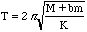 ,
(4.1)
,
(4.1)
where K is the spring constant. Calculate the following for small elongations of the spring, and for small values of m/M, b=1/3.
[You should get
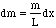 ].
].
Hint: The anchored end of the spring is always stationary, so for, say, x = 0, then v = 0. The end where the mass M is attached moves at the same velocity as M, so for x = L, then v = V. Thus, for example at a point halfway between, at x = L/2, then v = V/2. You may assume that the velocity varies linearly from x=0 to x=L.
[You should get
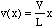 .]
.]
[i.e. integrate
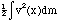 with limits for x=0 to x=L]
with limits for x=0 to x=L]
Consider a rigid body rotating around an axis. If the angular velocity
is [[omega]], each point in the body will move with linear speed
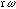 .
.
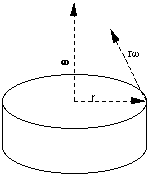
Figure 4.1
where r is the perpendicular distance of the point from the axis. The total angular momentum L of the rotating body points along the axis and is equal in magnitude to,
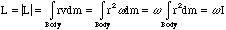 ,
(4.2)
,
(4.2)
where
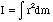 is called the moment of inertia of the body about the axis of rotation.
is called the moment of inertia of the body about the axis of rotation.
In the m.k.s. system of units, the units of I are
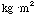 .
If the axis of rotation is chosen to be through the center of mass of the
object, then the moment of inertia about the center of mass axis is call
Icm. For example, Icm=
.
If the axis of rotation is chosen to be through the center of mass of the
object, then the moment of inertia about the center of mass axis is call
Icm. For example, Icm=
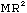 for a thin ring of mass M and radius R for the case where the
axis is the symmetry axis of the ring
for a thin ring of mass M and radius R for the case where the
axis is the symmetry axis of the ring
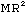 .
Table 4.1 are examples of Icm for different kinds of objects (e.g. see
Ohanian, Chapter 12).
.
Table 4.1 are examples of Icm for different kinds of objects (e.g. see
Ohanian, Chapter 12).
The parallel-axis theorem relates the moment of inertia Icm about an axis through the center of mass to the moment of inertia I about a parallel axis through some other point. The theorem states that,
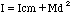 ,
(4.3)
,
(4.3)
Object Axis Icm ------------------------------------------------------------------------ Thick Ring Symmetry Axis(Mass M, radii R1 and R2) Disk Symmetry Axis
(Mass M, radius R) Thin Spherical Shell About a Diameter
(Mass M, radius R) Solid Sphere About a Diameter
(Mass M, radius R) ------------------------------------------------------------------------
Table 4.1
where M is the total mass of the body and d is the distance between the two axis. This implies Icm is always less than I about any other axis.
When working with rotational motion for rigid bodies, many of the equations are identical to the equations for linear motion with proper substitutions. The angular velocity is used instead of linear velocity, and the moment of inertia I is used instead of the mass M.
The following is a summary of the correspondence between linear and rotational kinematics for rigid bodies:
Linear Kinematics Rotational Kinematics ---------------------------------------------------------------------- Velocity : v Angular Velocity :Mass : M Moment of Inertia : I Momentum : P = Mv Angular Momentum : L = I
Kinetic Energy : K =
Kinetic Energy : K =
----------------------------------------------------------------------
Table 4.2
The apparatus consists of a rotary table on which you can mount
the object whose moment of inertia is to be measured. A torsion spring
restricts the motion of the table and provides a restoring torque. If the
table is rotated by an angle
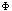 ,
the torque acting on it will be equal to,
,
the torque acting on it will be equal to,
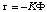 ,
(4.4)
,
(4.4)
where K is a constant which has to be measured. If the sum of the
moment of inertia of the table
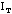 and of the object on top I is equal to
and of the object on top I is equal to
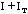 ,
the table will perform a rotary oscillation with the frequency,
,
the table will perform a rotary oscillation with the frequency,
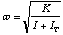 , (4.5)
, (4.5)
which corresponds to a period,
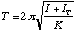 . (4.6)
. (4.6)
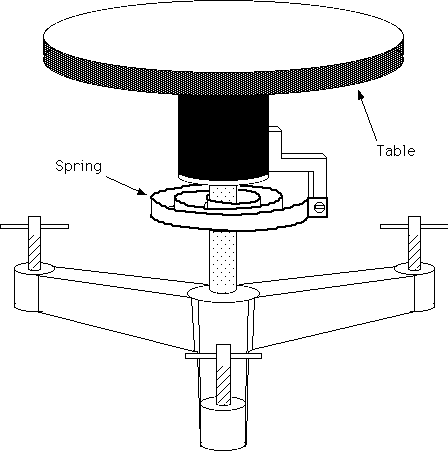
Figure 4.2
Note that there are two unknown parameters of the apparatus
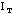 and K. To determine these, you need to measure the period of the bare
table
and K. To determine these, you need to measure the period of the bare
table
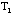 ,
and the period
,
and the period
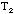 resulting when an object of a known moment of inertia
resulting when an object of a known moment of inertia
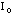 is set on the table.
is set on the table.
Now,
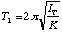 ,
(4.7)
,
(4.7)
and,
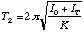 .
(4.8)
.
(4.8)
So by squaring both equations and then adding we obtain,
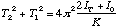 ,
(4.9)
,
(4.9)
and by subtracting,
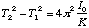 .
(4.10)
.
(4.10)
This solves for one of the table constants,
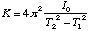 .
(4.11)
.
(4.11)
The other can be obtained by dividing,
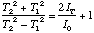 ,
(4.12)
,
(4.12)
or
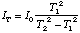 .
(4.13)
.
(4.13)
By this means the unknown constants of the table
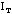 and K can be determined if a body of known moment of inertia is
available. Note that the moment of inertia
and K can be determined if a body of known moment of inertia is
available. Note that the moment of inertia
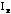 of an unknown object can be found using the above equation, i.e.,
of an unknown object can be found using the above equation, i.e.,
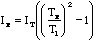 ,
(4.14)
,
(4.14)
where
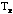 is the period with the unknown object on the table.
is the period with the unknown object on the table.
 .
.
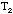 .
.
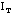 for the table using equation (4.13). [In this lab K is somewhere
between 0.25 and 1.0 N/m].
for the table using equation (4.13). [In this lab K is somewhere
between 0.25 and 1.0 N/m].
 with
theoretical methods and compare it to the measured value taken when the disk
axis is centered on the table. Use the difference as an estimate of the
errors.
with
theoretical methods and compare it to the measured value taken when the disk
axis is centered on the table. Use the difference as an estimate of the
errors.
It is often assumed that a long spiral spring obeys Hooke's law if it is not stretched too far. If the spring is hung vertically from a fixed support and a mass is attached to its free end, the mass can then oscillate vertically with simple harmonic motion. The period of oscillation depends upon the mass M accelerated and the force constant K of the spring. The period is measured by lifting the weight and letting it go. The time it takes for the weight to return to the start position is defined as the period. If the mass of the spring m is negligible, the period T is,
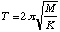 . (4.15)
. (4.15)
However, since the spring also moves, its mass m if not negligible, must enter into the equation for the period. Since the equation must remain dimensionally correct, the mass of the spring can only enter in the following way,
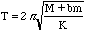 ,
(4.16)
,
(4.16)
where b is a constant number without dimensions.
According to Hooke's Law, the extension of the spring should be proportional to the applied force on the spring. F = - Kx, where F is the force, x is the extension, and K is the force constant of the spring.
Be careful not to destroy the spring!by over- stretching it. NEVER USE MORE THAN 100g OF WEIGHT! Attach the weights gingerly to the oscillator. Set the oscillator into motion by LIFTING the weight gently (thus compressing the spring) and then releasing.
Error Analysis. You may neglect the errors in the masses. Just plot the errors in T on the graph and estimate the errors from the graph as needed.