Coulomb's Law
Purpose
To verify the proportionality of Coulomb's Law that the electric force
between two point charges is directly
proportional to the product of the charges and is indirectly proportional to
the square of the distance between them.
Introduction
Coulomb's Law gives us the static electrical force F, exerted by a point
charge Q1 on another point charge Q2 in terms of r, the distance between them
:
F = Q1 Q2 / (4 pi eo r^2)
In this experiment, we will verify this law and enroute learn how to use an
optical lever to magnify a small rotation into a large displacement. Finally we
will learn about systematic errors and how to correct for them.
PreLab Homework
The prelab homework must be done at home and handed to the lab TA before
you start the lab.
Questions :
- The electric force as stated above depends on the distance r, in a certain
way. Can you think of another force in nature which also obeys an " inverse
- square" law ?
- Plot the function y = x^n (for n = -2 ) on log - log paper (to be found in a
folder outside of the lab) and obtain the value of n from this plot.
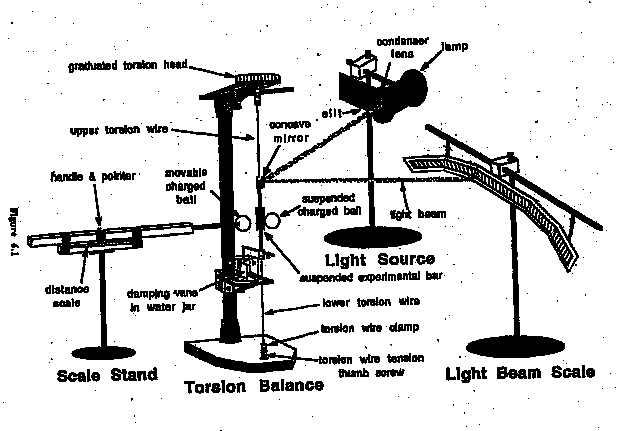
The Experiment
Description
The verification of Coulomb's Law proceeds as follows :
Procedure
The actual experiment will be executed as follows :
I. Setting it up
- Clean the spheres and insulators with alcohol; dry them with tissue
paper and drier. This ensures that no charges apart from the ones we place on
the spheres influence the experiment.
- The optical lever system for measuring theta must be adjusted. Adjust the torsion
head so that the wire is taut and the damping vane is at the center of the
beaker so that it can move without being obstructed by the glass walls.
- Adjust the lamp and place the stand of the scale 1.2 m away from the mirror to
get a sharp image about 25 cm from the right end (looking from the mirror) of
the circular scale, on which each graduation is 1 cm. make sure that the image
does not go off the scale for maximum deflection theta0 of the light beam.The light
source, the mirror and the scale should all be in a horizontal plane.
II. Measuring the relaxation time of the torsion fiber
Although we are interested in the static deflection theta of the optical
lever system to infer the force F, we have to acknowledge that this system is a
torsion oscillator and the transient behavior to static changes must be
determined. There is an oscillatory period t0 and a damping or relaxation time
tr. The angular displacement due to these transients is given by :
theta( t ) = theta0 exp ( - t / tr ) cos ( 2 pi t / t0 )
from where we can see that at time t = t r
theta( t ) = theta0 exp ( -1 ) ~ theta0/3
(Here we have used the fact that for critical damping, t0 ~ tr ). So the reason
we wait till the displacement becomes a third of the original theta0 is that the
time interval t then equals tr. tr is called the " relaxation time" and is
the approximate time that the torsion oscillator takes to settle down to its
equilibrium value. Actually 1/3 is here an approximation for the number 1/e =
1/ 2.71... and is therefore not fundamental and is only an approximation.
Each time we vary the charge or the distance, we should wait ~ 3tr seconds
before taking down a reading.
- Touch the spheres with the grounding probe - this makes them totally
neutral.
- Perturb the optical lever system by blowing on the sphere attached to the
torsion. Obtain about 15-20 cm displacement (theta0). Note theta0 , and start the
timer. Stop when displacement theta = theta0 /3. The time measured will then equal tr.
III. Measuring the leakage of charge
Because of air currents and humidity, charge tends to leak off from the
spheres. The leakage is not negligible and has to be accounted for. This will
enable you to make a correction to the charge in your later measurements.
- Adjust the movable sphere such that the pointer on the scale reads 3.0 cm ;
bring the movable sphere and stand as near as you can to the sphere on the
torsion without making them touch. Since the radius of each sphere is 1.5 cm
the distance between their centers ( 3 cm ) can now be directly read off the
scale ( 3 cm ! ). The heights of the spheres from the table should be equal. The
stand should not be moved for the rest of the experiment.
- Rub the lucite rod with silk. " Scrape" ( your TA will demonstrate this)
across the sphere attached to the torsion to transfer charge. This will introduce an opposite " image" charge on the sphere attached to the
fiber. It will move towards the movable sphere attached to the scale, finally
touching it. Once the spheres touch, the charges will be equally distributed
between them and since they now will have the same charge, they will
begin to repel each other. The sphere on the torsion fiber will now
begin to move away from the movable sphere, and the light image will register a
deflection on the circular scale. You should keep increasing the charge till theta
= theta0 ~ 25 cm ( This is not critical ; 20 or 32 cm will work just as well). Start
the timer.
- Note the decrease of theta as time elapses; that is, record theta vs. t every
centimeter as theta = 25, 24, 23, ..., 0 cm. The leakage of charge might turn out to be
an exponential decay, i.e. the displacement at any time t would be given by :
theta( t ) = theta0 exp ( - t / td )
where theta0 is the initial displacement and the decay is characterized by a "time
constant" td . To find td we wait for the displacement to become a third of
initial value just as we did for tr.
- Plot a normalized deflection [ theta / theta0 ] "decay curve" on semi-log paper
provided by the TA. If the deflection is exponential, you should observe a
straight line. Whatever curve you measure will be used to correct for leakage
in later readings of theta in the Q1 and r sections (Parts IV and V below ) by
reading off the fraction of charge that has been lost ( the amount by which the
displacement has resultantly decreased ) and adding it to whatever theta you have
measured.
IV. Varying the charge Q1
Now we will actually begin making measurements to test Coulomb's Law. In
this section we vary the charge Q1.
- Ground spheres ; obtain equilibrium.
- Set sphere on scale to 3.5 cm. Charge spheres to get 20-30 cm
deflection.
- Set sphere on scale to 5 cm.Start timer ; note, after the transient dies
out. (Do not stop the timer.)
Note :If we set r = 5 cm before charging , the
amount of charge we will have to put on the spheres to get a 20-30 cm deflection is going
to be rather large - remember that the electric force F ( here ) is
proportional to 1/r^2 , i.e., it weakens rapidly with distance. If
we still keep r = 3.5 cm after charging , we might find ourselves in
the regime where there are complications due to the image charges
that the spheres induce in each other. Hence we start taking
readings with r = 5 cm.
- Ground test sphere ; touch it to the movable sphere, thus halving its
charge. Record , t when the displacement stabilizes.
Here we used the fact that the uncharged test sphere, when brought into contact
with the sphere on the torsion fiber ( carrying charge Q1 ) will take away half
its charge, leaving it with Q1 /2. To vary Q1 further, we will ground
the test charge and touch it to Q1 /2, halving it to Q1 /4 and then record
the corresponding , t.
- Repeat the halving procedure until you reach Q1 /8 or the deflection is
too small to measure.
V. Varying the distance r between the spheres
The procedure is similar to that of Part IV above.
- Ground spheres ; obtain equilibrium.
- Set the movable sphere to 3.5 cm.Charge spheres to get 20-30 cm deflection.
- Set the movable sphere to 5 cm to make the image charge effects small. start timer; note , t after the transients have died down. Do not stop the timer.
- Set the sphere on the scale to 10, 15 & 20 cm ; record , t after each change of scale.
VI. Leakage of charge ( again )
Due to possible changes in humidity and other conditions of the air we
measure the decay curve and plot it on the same graph as Part III above.
Data Analysis
- Compare the before and after plots of normalized
deflection [ /0 ] vs. time t. If they are different use their average - which
is NOT just a line half - way between the two - as the correction for the
corresponding - values. The difference between the average and the two curves
will be the error (i.e. the error bars will touch both the plotted lines ).
- Plot the deflection ( decay-corrected ) vs. charge data taken in part IV
above on linear - linear paper.
- Plot the deflection ( decay - corrected ) vs. separation data taken in part V
above on log - log paper. Here :
- You may wish to neglect the points for small separations where the image
charge effects are the largest and the graph might deviate from a straight
line. Draw a best - fitting straight line. What is the slope of this line ?
- Do the results indicate a " power law" ? If so, what is your best
estimate of the exponent ?
Send comments, questions and/or suggestions via email to wolfs@nsrl.rochester.edu.

