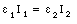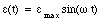
The current from a 110-V outlet is an oscillating function of time. This type is called Alternating Current or AC. A source of AC is symbolized by a wavy line enclosed in a circle (see Figure 34.1). The time dependence of the AC or the emf of the AC source is of the form
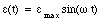
where [epsilon]max is the maximum amplitude of the oscillating emf and [omega] is the angular frequency.
Figure 34.2 shows a single-loop circuit with a source of alternating emf and a resistor. The current through the resistor will be a function of time. The magnitude of this current can be obtained via Kirchhoff's second rule which implies that
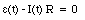
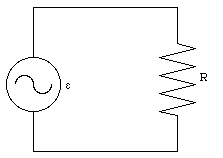
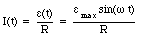
Equation (34.3) shows that the current oscillates in phase with the emf.
The power dissipated in the resistor depends on the current through and the voltage across the resistor and is therefore also a function of time:
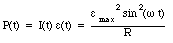
The average power dissipated in the resistor during one cycle is equal to
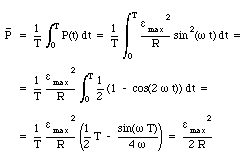
In the last step of the derivation of eq.(34.5) we used the relation between the period T and the angular frequency [omega] (T = 2[pi]/[omega]). Often, eq.(34.5) is written in terms of the root-mean-square voltage [epsilon]rms which is defined as
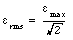
In terms of [epsilon]rms we can rewrite eq.(34.5) as
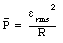
The root-mean-square voltage [epsilon]rms of the AC source is the value of the DC voltage that dissipates the same power in the resistor as the AC voltage with a maximum voltage equal to [epsilon]max. The household voltage of 115 Volt is the root-mean-square voltage; the actual peak voltage coming out of a household outlet is 163 V.
Figure 34.3 shows a capacitor connected to a source of alternating emf. The charge on the capacitor at any time can be obtained by applying Kirchhoff's second rule to the circuit shown in Figure 34.3 and is equal to
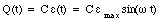
The current in the circuit can be obtained by differentiating eq.(34.8) with respect to time
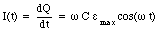
It is customary to rewrite eq.(34.9) as
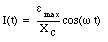
where
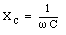
is called the capacitive reactance. Note that eq.(34.10) is very similar to eq.(34.3) if the resistance R is replaced by the capacitive reactance XC. The power delivered to the capacitor is equal to
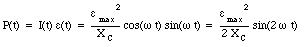
The power fluctuates between positive and negative extremes, and is on average equal to zero. These fluctuations corresponds to periods during which the emf source provides power to the battery (charging) and periods during which the battery provides power to the emf source (discharging).
Figure 34.4 shows a circuit consisting of an inductor and a source of alternating emf. The self-induced emf across the inductor is equal to LdI/dt. Applying Kirchhoff's second rule to the circuit shown in Figure 34.4 we obtain the following equation for dI/dt:
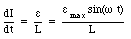
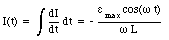
The current is again 90deg. out of phase with the emf, but this time the emf leads the current. Equation (34.14) can be rewritten as
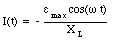
where
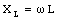
is called the inductive reactance. The power delivered to the inductor is equal to
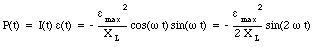
and the average power delivered to the inductor is equal to zero.
Consider the circuit shown in Figure 34.5. The emf is of the form [epsilon]0 sin([omega]t). In terms of this emf and the capacitance C and the inductance L, find the instantaneous currents through the capacitor and the inductor. Find the instantaneous current and the instantaneous power delivered by the source of emf.
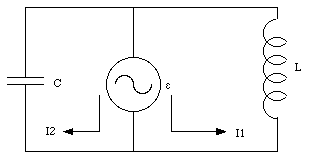
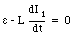
Applying Kirchhoff's second rule to loop number 2 we obtain
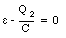
Equation (34.18) can be used to determine I1:
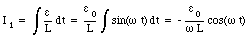
Equation (34.19) can be differentiated with respect to time to obtain I2:
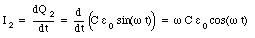
The current delivered by the source of emf is the sum of I1 and I2
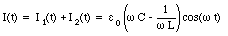
The power delivered by the source of emf is equal to
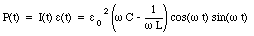
Figure 34.6 shows a single-loop circuit consisting of an inductor and a capacitor. Suppose at time t = 0 s the capacitor has a charge Q0 and the current in the circuit is equal to zero. The current in the circuit can be found via Kirchhoff's second rule which requires that
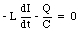

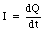
Substituting eq.(34.25) into eq.(34.24) we obtain
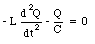
or
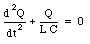
A solution of eq.(34.27) is
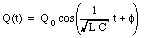
where [phi] is a phase constant that must be adjusted to fit the initial conditions. The current in the circuit can be obtained by substituting eq.(34.28) into eq.(34.25):
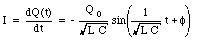
The initial conditions for the circuit shown in Figure 34.6 are
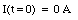
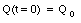
These boundary conditions are satisfied if [phi] = 0. In this case, the charge and the current in the LC circuit are given by
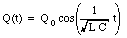
and
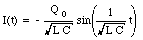
The energy stored on the capacitor is a function of time since the charge on it is a function of time. The energy stored is equal to
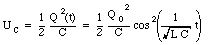
The energy stored in the inductor is also time dependent since the current through it is a function of time. The energy stored is equal to
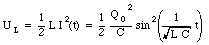
Equation (34.34) and eq.(34.35) show that the maximum energy is stored in the inductor when the energy stored in the capacitor is zero and vice-versa. The total energy of the circuit can be obtained by summing the energy stored in the capacitor and the energy stored in the inductor:
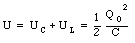
Equation (34.36) shows that the energy stored in the circuit is conserved. This is expected since no Joule heat will be generated in a circuit in which none of the elements has any resistance.
In practice, the circuit shown in Figure 34.6 will have some resistance (even good conductors will have a finite resistance). A realistic LRC circuit is shown in Figure 34.7. Applying Kirchhoff's second rule to the circuit shown in Figure 34.7 we obtain
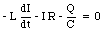
Since the current I is equal to dQ/dt we can rewrite eq.(34.37) as
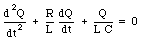
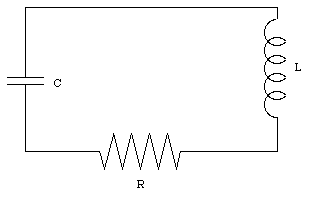
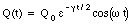
The constant [gamma] can be determined by substituting eq.(34.39) into eq.(34.38):
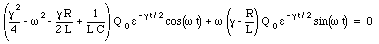
This equation has to be satisfied at all times. This will only be the case if the terms within the parenthesis are equal to zero:
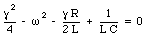
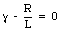
The constant [gamma] is determined by eq.(34.42)
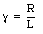
The angular frequency [omega] can be obtained from eq.(34.41) by substituting eq.(34.43) for [gamma]
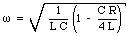
Equation (34.39) shows that the presence of the resistor in the circuit will produce damped harmonic motion. The damping constant [gamma] is proportional to the resistance R (see eq.(34.43)). The change in the energy of the system can be studied by looking at the maximum charge on the capacitor. At time t = 0 s the capacitor is fully charged with a charge equal to Q0 and the energy stored in the capacitor is equal to
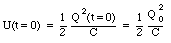
After one cycle (t = 2[pi]/[omega]) the maximum charge on the capacitor has decreased. This implies that also the energy stored on the capacitor has decreased
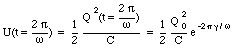
The relative change in the electrical energy of the system is therefore equal to
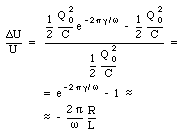
The loss of electrical energy in a LRC circuit is usually expressed in terms of the quality Q-value"
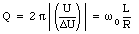
A high quality factor indicates a low resistance and consequently a small relative energy loss per cycle.
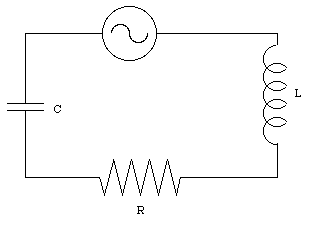
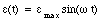
Applying Kirchhoff's second rule to the circuit shown in Figure 34.8 produces the following relation
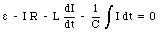
Under steady-state conditions, the current in the circuit will oscillate with the same angular frequency [omega] as the source of emf, but not necessarily in phase. The most general solution for the current is therefore
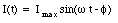
where [phi] is called the phase angle between the current and the emf. The maximum current Imax and the phase angle [phi] can be determined by substituting eq.(34.51) in eq.(34.50):
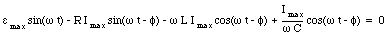
Equation (34.52) can be rewritten using trigonometric identities as
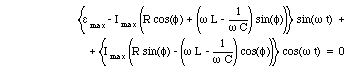
This equation can only be satisfied if the expressions in the brackets are equal to zero. This requires that
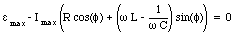
and
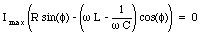
Eq.(34.55) can be used to determine the phase angle:
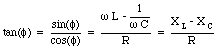
Equation (34.54) can be used to determine the maximum current:
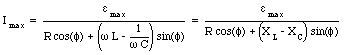
Substituting eq.(34.56) into eq.(34.57) we obtain for the maximum current
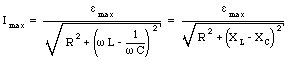
The quantity
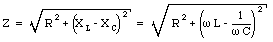
is called the impedance of the LCR circuit.
Equation (34.58) shows that the maximum amplitude is achieved when
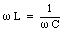
The maximum amplitude of the current is
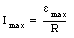
The system will reach its maximum amplitude when the driving frequency [omega] of the applied emf is equal to
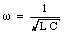
This frequency is the natural frequency of the LC circuit discussed previously. When the system is driven at the natural frequency, it is said to be in resonance.
A short cut that can be used to determine the amplitude and phase of current in an AC circuit is the phasor diagram. In a phasor diagram the amplitude of a sinusoidal function is represented by a line segment of length equal to its amplitude. The phase is represented by the angle between the line segment and the horizontal axis. The sum of voltage drops across the components of the circuit is then equivalent to the vector sum of the phasors. To illustrate the use of phasor diagrams we determine the amplitude and phase of the LCR circuit just discussed. The applied emf and induced current are given by the following equations:
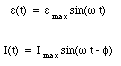
The voltages across the resistor, the capacitor and the inductor are equal to
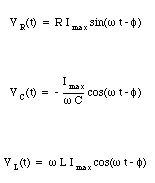
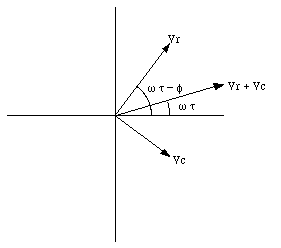
The three phasors corresponding to these three voltages are shown in the phasor diagram in Figure 34.9. The voltage drop across the resistor has the same phase as the current. The vector sum of these three vectors is also indicated and should be equal to the applied emf. The amplitude of the vector sum of the three phasors must be equal to the amplitude of the applied emf. Thus
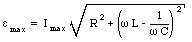
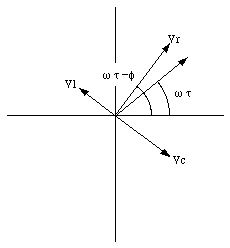
The phase of the vector sum of the phasors in Figure 34.9 is equal to [omega]t, and the angle between the current (and the phasor representing the voltage drop across the resistor) and the vector sum of the phasors is equal to the phase angle [phi]. From Figure 34.9 it is obvious that
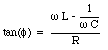
Consider the circuit shown in Figure 34.10. The oscillating source of emf delivers a sinusoidal emf of amplitude 0.80 V and frequency 400 Hz. The inductance is 5.0 x 10-2 H, and the capacitances are 8.0 x 10-7 F and 16.0 x 10-7 F. Find the maximum instantaneous current in each capacitor.
Consider first the two capacitors. The emf across each of the capacitor must always be the same. This implies that
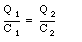
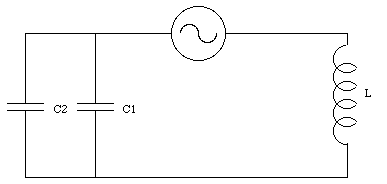
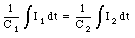
or
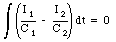
Equation (34.69) can only be true at all times if the integrand is equal to zero. This requires that
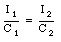
In order to determine the maximum current in the circuit we use the phasor technique just discussed. Consider the phasor diagram shown in Figure 34.11. The phasor labeled I indicates the current in the circuit. The voltages across the inductor and the capacitor are 90 degrees out of phase with the current and are indicated in Figure 34.11 by the phasors labeled VL and VC. The total voltage drop across the circuit elements (vector sum of VL and VC) is also 90 degrees out of phase with the current. Since the total voltage drop across the circuit elements must be equal to the applied emf, we conclude that the phase angle between the current and the emf is +/- 90 degrees. The sign depends on the values of inductance, the capacitance and the angular frequency of the emf.
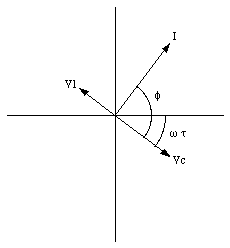
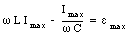
Equation (34.71) can be used to determine the maximum current in the circuit:
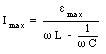
The capacitance C used in eq.(34.72) is the net capacitance of the parallel network consisting of capacitor C1 and capacitor C2 (C = C1 + C2). The sum of the currents flowing through capacitors is equal to the maximum current in eq.(34.73). To determine the current through capacitor C1 and capacitor C2 we can combine eq.(34.72) and eq.(34.70). In this manner we obtain
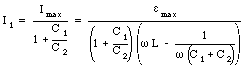
and
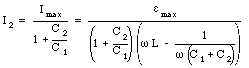
An RC circuit consists of a resistor with R = 0.80 [Omega] and a capacitor with C = 1.5 x 10-4 F connected in series with an oscillating source of emf. The source generates a sinusoidal emf with emax = 0.40 V and angular frequency equal to 9 x 103 rad/s. Find the maximum current in the circuit. Find the phase angle of the current and draw a phasor diagram, with the correct lengths and angles for the phasors. Find the average dissipation of power in the resistor.
The applied emf and the potential drops across the circuit elements in the RC circuit are listed in eq.(34.75).
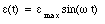
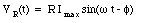
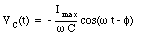
The phasors representing the voltage drops across the resistor and across the capacitor are shown in Figure 34.12. The vector sum of these phasors is also indicated. The magnitude of the vector sum of the phasors must be equal to the magnitude of the applied emf. Thus
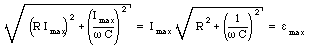
The maximum current is thus equal to
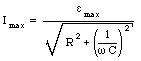
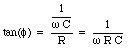
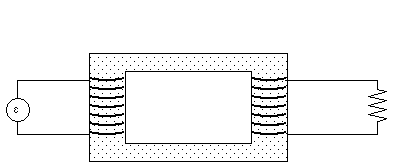
A transformer consists of two coils wound around an iron core (see Figure 34.13). The iron core increases the strength of the magnetic field in its interior by a large fraction (up to 5000) and as a consequence, the field lines must concentrate in the iron. One of the coils, the primary coil, is connected to a source of alternating emf.
The emf induced in the primary coil is related to the rate of change of magnetic flux (Faraday's law of induction):
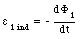
Applying Kirchhoff's second rule to the primary circuit, we conclude that the induced emf in the coil must be equal to the applied emf. Thus
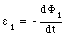
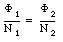
or
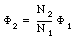
The change in the enclosed flux of the primary coil will be related in the same way to the change of flux in the secondary coil:
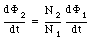
The emf induced across the secondary coil can be obtained using Faraday's law and can be expressed in terms of the emf in the primary circuit:
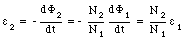
This emf is available to the various loads in the secondary circuit.
If the secondary circuit is open, no current will flow in it, and the primary circuit is nothing else than a single-loop circuit with an alternating source of emf and an inductor. The average power dissipated by the emf in such a circuit is zero, and consequently the transformer does not consume any electric power.
If the secondary circuit is connected to a load, a current will flow. This induced current will change the magnetic flux in the transformer and induce a current in the primary coil. If this occurs, the primary circuit will consume power. In an ideal capacitor, the power delivered by the source of emf in the primary circuit equal the power that the secondary circuit delivers to its load. Thus