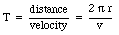
An electron moving in an orbit around a nucleus produces an average current along its orbit. As a consequence we can associate a magnetic moment with the orbiting electron. Suppose the electron is moving with a velocity v in an orbit with radius r. The period of this motion is equal to
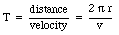
During one period T the charge e will pass each given point on the orbit. The current associated with this orbit is therefore equal to
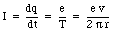
The magnetic moment associated with this current is equal to
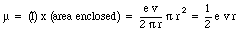
It is common to specify the orbit of an electron in terms of its angular momentum L. Using the definition of the angular momentum L we can relate the electron velocity v and the radius of its orbit r to the angular momentum L in the following manner:
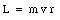
where m is the mass of the electron. Using eq.(33.4) we can express the magnetic moment of the electron in terms of the angular momentum L:
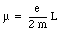
The magnetic moment of the electron is thus proportional the angular momentum
L. The angular momentum of the electron is quantized, and the only possible
values are nh where n is an integer (n = 0, 1, 2, 3, ...) and
h is a constant (h = 1.06 .
10 -34 J s). The magnetic moment of an electron with angular
momentum L = 1 is equal to
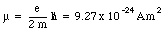
Since this magnetic moment is associated with the orbital motion of the electron around the nucleus it is called the orbital magnetic moment. Another contribution to the magnetic moment is due to the rotational motion of the electron. Classically we can regard an electron as a small ball of negative charge spinning around its axis. The intrinsic angular momentum, generated by the electron spin, is equal to
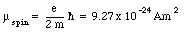
This constant is also called the Bohr magneton.
The total magnetic moment of an atom is equal to the vector sum of the orbital magnetic moments and the intrinsic magnetic moments of all its electrons. The contribution of the nuclear magnetic moment is small and often can be neglected. Each atom acts like a magnetic dipole and produces a small, but measurable magnetic field.
a) Two electrons are separated by a distance of 1.0 x 10 -10 m. The first electron is on the axis of spin of the second. What is the magnetic field that the magnetic moment of the second electron produces at the position of the first ?
b) The potential energy of the magnetic moment of the first electron in this magnetic field depends on the orientation of the electrons. What is the potential energy if the spins of the two electrons are parallel ? If anti parallel ? Which orientation has the least energy ?
a) Figure 33.1 shows the orientation of the two electrons. The z-axis is defined to coincide with the spin of electron 2. With each spinning electron a magnetic dipole moment can be associated. Due to the negative charge of the electron the dipole moment is pointed in a direction opposite to that of the spin of the electron and it has a magnitude equal to uspin = 9.27 x 10 -24 Am2. The magnetic field generated by electron will be the magnetic field generated by a dipole with dipole moment uspin. On the z-axis (and for z >> Re) the field strength will fall of as 1/z3 and at z = 1.0 x 10 -10 m has a strength equal to
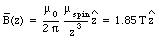
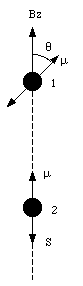
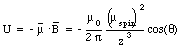
where [theta] is the angle between the dipole moment and the magnetic field. The potential energy of electron 1 reaches a maximum value when [theta] = [pi] and a minimum value when [theta] = 0. Evaluating equation (33.9) for these extreme cases yields
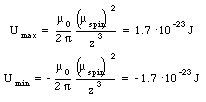
The potential energy will have a minimum value when the spins are parallel and a maximum value when the spins are anti-parallel.
Even though each atom in a material can have a magnetic moment, the direction of each dipole is randomly oriented and their magnetic fields average to zero. If the material is immersed in an external magnetic field, the dipoles will tend to align themselves with the field in order to minimize the torque exerted on them by the external magnetic field. The atoms in the material will produce an extra magnetic field in its interior that has the same direction as the external magnetic field. This increase in strength of the magnetic field can be quantified in terms of the permeability constant [kappa]m:
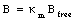
where Bfree is the external magnetic field. The definition of the permeability constant (see eq.(33.11)) shows that [kappa]m >= 1. For all paramagnetic materials the permeability constant is very close to 1, and as a consequence, the increase in the magnetic field strength is rather small.
Show that the self-inductance per unit length of a very long solenoid filled with a paramagnetic material is equal to [kappa]m u0 n2 [pi] R2, where n is the number of turns of wire per unit length and R is the radius of the solenoid.
The magnetic field in an empty solenoid is equal to
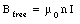
When the solenoid is filled with a paramagnetic material the strength of the magnetic field will increase (see eq.(33.11)) and will be equal to
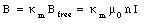
The magnetic flux enclosed by a section of the solenoid of unit length is equal to
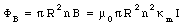
The change in enclosed magnetic can be obtained from eq.(33.14) by differentiating both sides with respect to time
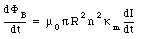
The emf induced by this change in magnetic flux can be calculated using Faraday's law
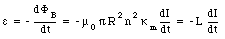
From eq.(33.16) we conclude that the self-inductance of the solenoid filled with a paramagnetic material is equal to
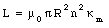
The alignment of the spins of some of the electrons in a ferromagnetic material will increase the magnetic field in this material in much the same way as the alignment of the orbital magnetic dipole moments of atoms increases the field strength in a paramagnetic material. In a ferromagnetic material the degree of alignment of the electron spins between neighboring atoms is high as a result of a special force that tends to lock the spins of these electrons in a parallel direction. This force is so strong that the spins remain aligned even when the external magnetic field is removed. Materials with such properties are called permanent magnets. The force that is responsible for the alignment of the electron spins occurs in only five elements:
The degree of alignment of the spins in a ferromagnetic material after the external magnetic field has been removed depends on the temperature. An increase in the temperature of the material will increase the chance of random rearrangement of the magnetic dipoles. Above a certain temperature, called the Curie temperature, the magnetism of the ferromagnet disappears completely.
Under conditions of maximum magnetization, the dipole moment per unit volume of cobalt is 1.5 x 10 5 Am2/m3. Assuming that this magnetization is due to completely aligned electrons, how many such electrons are there per unit volume ? How many aligned electrons are there per atom ? The density of cobalt is 8.9 x 10 3 kg and the atomic mass is 58.9 g/mole.
The dipole moment of 1 m3 of cobalt is equal to 1.5 x 10 5 Am2. Each aligned electron contributes a dipole moment of 9.27 x 10 -24 Am2. The number of aligned electrons is thus equal to
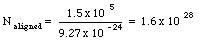
The number of atoms in 1 m3 of cobalt is equal to
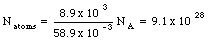
Comparing eq.(33.18) and eq.(33.19) we conclude that the total number of aligned electrons per atom is equal to 0.18.
In a diamagnetic material the magnetization arises from induced magnetic dipoles. This in contrast to the paramagnetic and ferromagnetic materials where the magnetic properties are determined by the alignment of permanent magnetic dipoles. In a diamagnetic material the dipole moments of the atoms do not align themselves with the magnetic field, but their strength is changed by the external field.
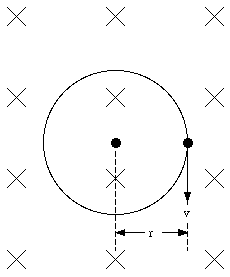
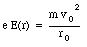
When the magnetic field is turned on, the electron will experience in addition to the electric force a magnetic force equal to
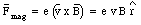
This force is radially directed (inwards or outwards depending on the direction of v0 with respect to B). The condition for uniform circular motion is now
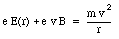
Assuming that the size of the orbit of the electron does not change, we conclude that the effect of the magnetic field is a change in the velocity of the electron. Combining eq.(33.22) and eq.(33.20) we obtain
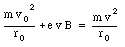
It is convenient to express the velocity of the electron in terms of its angular frequency
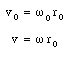
Substituting the expressions for v0 and v from eq.(33.24) into eq.(33.23) we obtain
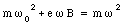
or
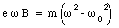
The change in frequency [Delta][omega] is defined via the following relation
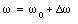
Substituting eq.(33.27) into eq.(33.26) we obtain
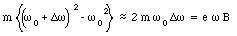
or
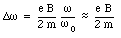
This frequency is called the Larmor frequency, and indicates the maximum change in the velocity of the orbital electrons when an external magnetic field is applied. As a result of the change in the velocity of the orbital electrons there will be a change in the orbital magnetic moment. The orbital magnetic moment before the external magnetic field is applied can be calculated using eq.(33.3)
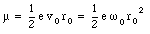
When an external magnetic field is applied the angular frequency [omega] will change by [Delta][omega]. Equation (33.30) shows that the associated change in the orbital magnetic moment is equal to
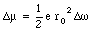
The change of the angular frequency can be positive or negative, depending on the direction of v0 with respect to the direction B. The angular frequency will increase if the direction of the field and the electron velocity are not related via the right-hand rule (field into paper in Figure 33.2). The change in the magnetic moment of the dipole is such that the net field strength (external + orbital magnetic field) is lowered. This means an increase in the orbital magnetic moment if the orbital magnetic field is directed in a direction opposite to the external field, and a decrease in the orbital magnetic moment if the orbital magnetic field is directed in the same direction as the external field. In both cases the total magnetic field strength is reduced, and, consequently, the permeability constant [kappa]m is less than 1. For most diamagnetic materials the permeability constant is very close to 1 (1 - [kappa]m ~ 1 x 10 -5).