
1. Batteries: Batteries convert chemical energy into electric energy. In a lead-acid battery the following reactions take place when the battery delivers a current:
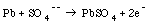
and
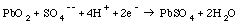
These reactions deposit electrons on the negative electrode and absorb electrons from the positive electrodes. The reactions in eq.(29.1) and eq.(29.2) will continue until the sulfuric acid is depleted. At this point the battery is discharged. The battery can be recharged by forcing a current through the battery in the reverse direction. The reverse of the reactions listed in eq.(29.1) and eq.(29.2) will then occur.
2. Electric Generators: Electric generators convert mechanical energy into electric energy. The principle of operation of electric generators will be discussed in Chapter 31.
3. Fuel cells: A mixture of chemicals are combined in the fuel cell. The chemical reactions that occur are
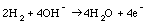
and
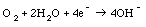
The net result of these reactions is the conversion of hydrogen and oxygen into water which is removed from the fuel cell in the form of water vapor. A fuel cell therefore burns fuel. The efficiency of the best fuel cells is about 45%.
4. Solar Cell: A solar cell converts the energy of the sunlight directly into electric energy. The emf of a silicon solar cell is 0.6 V. However, the amount of current that can be extracted is rather small.
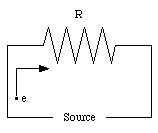
A source with a time-independent emf is represented by the symbol shown in Figure 29.2. The long line in Figure 29.2 represents the positive terminal of the source, while the short line represents the negative terminal.
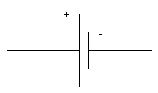
Around a closed loop in a circuit, the sum of all the emfs and all the potential changes across resistors and other circuit elements must equal zero.
In this sum, the emf of a source is reckoned as positive if the current flows through the source in the forward direction (from the negative terminal to the positive terminal) and negative if it flows in the backward direction. (Note: the direction of the current indicates the direction of the positive charge carriers).
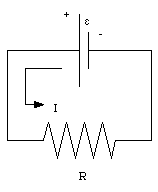
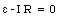
The current in the circuit is therefore equal to
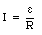
The procedure used to calculate the current flowing through a complicated circuit (with several resistors and emfs) is called the loop method. This procedure can be summarized as follows (see Figure 29.5 and Problem 29.17):
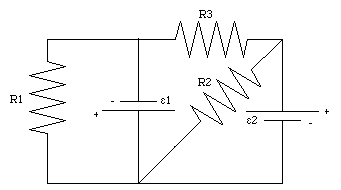
1. Regard the circuit as a collection of several closed current loops. The loops may overlap, but each loop must have at least one portion that does not overlap with other loops. In Figure 29.5 there are clearly 3 current loops.
2. Label the current in the loops I1, I2, I3, ....., and arbitrarily assign a direction to each of the currents. A useful policy can be to define the direction of the current in a loop as going from the positive terminal of the emf to the negative terminal of the emf (if an emf is present in the loop). This policy defines the direction of the current in loop 1, loop 2 and in loop 3 (see Figure 29.6).
3. Apply Kirchhoff's rule to each loop.
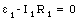
For loop 2 we find
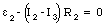
Finally, for loop 3 we find
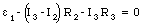
Using eq.(29.8) we can rewrite eq.(29.9) in the following manner
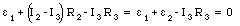
or
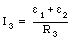
The current I2 can be obtained by substituting eq.(29.11) into eq.(29.8):
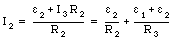
The current I1 can be obtained from eq.(29.7):
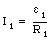
An alternative method to obtain the currents in a multi-loop circuit is the branch method which is based on Kirchhoff's first rule:
The sum of all currents entering a branch point of a circuit (where three or more wires merge) must be equal to the sum of the currents leaving the branch point.
The branch method involves the following steps (and is illustrated by discussing its application to problem 29.17):
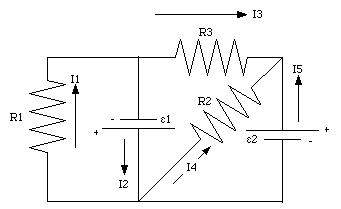
1. Regard the given circuit as a collection of branches which begin and end at the points where wires merge. The circuit in Figure 29.5 has five branches.
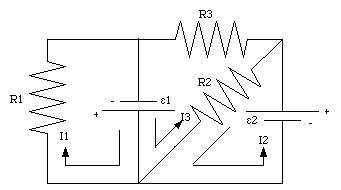
2. Label the currents in each branch I1, I2, I3, ....., and arbitrarily assign a direction to each of these currents. The currents in the five branches of circuit 29.5 are indicated in Figure 29.7.
3. Apply Kirchhoff's second law to each loop.
4. Apply Kirchhoff's first law to each branch point.
For loop 1 of the circuit shown in Figure 29.7 Kirchhoff's law dictates that
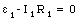
For loop 2 we obtain
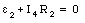
For loop 3 we obtain
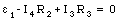
Apply Kirchhoff's first law to the three branch points of the circuit shown in Figure 29.7:
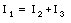
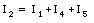
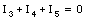
This procedure produces six equations with 5 unknown and the system is over-defined.
The current I1 can be obtained from eq.(29.14):
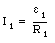
Equation (29.15) can be used to determine I4:
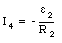
The current I3 can be obtained from eq.(), using the solution for I4 just derived (eq.(29.21)):
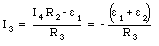
The current I2 can be obtained from eq.(29.17):
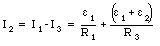
The current I5 can be obtained from eq.(29.19)
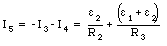
Note: since the loop method involves fewer unknown and fewer equations, it is usually quicker to use than the branch method.
Consider the circuit shown in Figure 29.8. Given that [epsilon]1 = 6.0 V, [epsilon]2 = 10.0 V, and R1 = 2.0 [Omega], what must be the value of the resistance R2 if the current through this resistance is to be 2.0 A ?
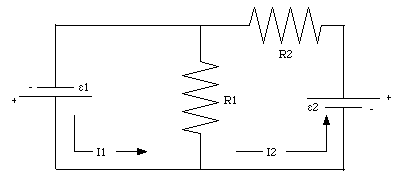
Consider the two loops shown in Figure 29.8. We will assume that the current in each loop flows in a counter clockwise direction (as shown in Figure 29.8). The voltage drop across resistor R1 is equal to R1 . (I1 - I2). The sum of all emfs and all potential drops across the resistors in loop 1 is
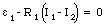
The sum of all emfs and all potential drops across the resistors in loop 2 is equal to
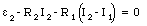
Equation (29.26) can be rewritten as
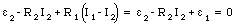
where we have used eq.(29.25). The current I2 is thus equal to
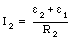
The problems states that [epsilon]1 = 6.0 V, [epsilon]2 = 10.0 V and I2 = 2.0 A. These values combined with eq.(29.28) can be used to determine R2:
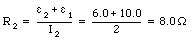
To keep a current flowing in a circuit, work must be done on the circulating charges. If a charge dq passes through a battery with emf [epsilon], the work done dW will be equal to
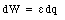
The rate at which the emf source does work is given by
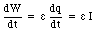
The rate of work is called the power P, and the unit of power is the Watt (W, 1 W = 1 VA).
The moving charges dissipate some of their energy when passing through resistors. Suppose the potential drop across a resistor is [Delta]V. For an electron moving through the resistor the loss of potential energy is equal to e . [Delta]V. The energy lost is converted into heat, and the rate at which energy is dissipated is equal to
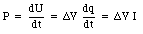
or
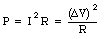
the conversion of electric energy into thermal energy is called Joule heating.
A high-voltage transmission line that connects a city to a power plant consists of a pair of copper cables, each with a resistance of 4 [Omega]. The current flows to the city along one cable, and back along the other.
a) The transmission line delivers to the city 1.7 x 105 kW of power at 2.3 x 105 V. What is the current in the transmission line ? How much power is lost as Joule heat in the transmission line ?
b) If the transmission line delivers the same 1.7 x 105 kW of power at 110 V, how much power would be lost in Joule heat ? Is it more efficient to transmit power at high voltage or at low voltage ?
a) The power delivered to the city, Pdelivered, is equal to 1.7 x 105 kW. The voltage delivered, [Delta]Vdelivered, is equal to 2.3 x 105 V. The current through the cables can determined by applying eq.(29.32):
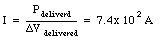
This is also the current flowing through the transmission cables. The electric energy dissipated in the cables is equal to
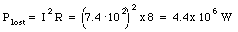
The power generated by the power plant must therefore be equal to
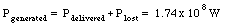
Comparing the power generated with the power delivered, we conclude that 98% of the generated power is delivered to the city.
b) If the voltage delivered to the city is 110 V, than current through the transmission cables must be equal to
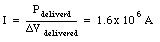
This current is roughly 2000 times the current flowing through the transmission cables if the power is delivered at high voltage. The power dissipated in the transmission cables is
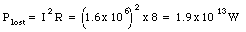
The power generated by the power plant must therefore be equal to
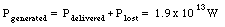
Comparing the power generated with the power delivered, we conclude that only 0.0009% of the generated power is delivered to the city. Clearly, our conclusion should be that the transmission of electric energy at high voltage is much more efficient that the transmission at low voltage. The voltage of the transmission line is therefore reduced to 110 V as close as possible to the house of the customer.
A 12-V battery of internal resistance Ri = 0.20 [Omega] is being charged by an external source of emf delivering 6.0 A.
a) What must be the minimum emf of the external source ?
b) What is the rate at which heat is developed in the internal resistance of the battery ?
a) The circuit describing this problem is shown in Figure 29.9. In Figure 29.9 [epsilon]1 is the emf of the battery being recharged, and [epsilon]2 is the emf of the recharger. Applying Kirchhoff's second rule to the single loop circuit we obtain the following relation between the charging current and the emfs:
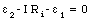
Equation (29.40) can be rewritten as
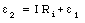
The emf of the battery to be recharged is [epsilon]1 = 12.0 V and it has an internal resistance Ri = 0.20 [Omega]. If the recharger is to deliver a current I = 6.0 A then the emf of the recharger must be equal to
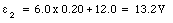
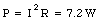
Suppose that a 12-V battery has an internal resistance of 0.40 [Omega].
a) If this battery delivers a steady current of 1.0 A into an external circuit until it is completely discharged, what fraction of the initial stored energy is wasted in the internal resistance ?
b) What if the battery delivers a current of 10.0 A ? Is it more efficient to use the battery at low current or at high current ?
a) Suppose the battery as an emf [epsilon]b and delivers a current I. The internal resistance of the battery is equal to Ri. The voltage drop across the internal resistance is equal to I Ri. The external voltage of the battery if thus equal to ([epsilon]b - I Ri). The power delivered by the battery to the external circuit is therefore equal to

The total power delivered by the emf is equal to
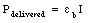
The fraction of the total delivered power that is dissipated in the internal resistance of the battery is equal to
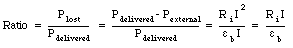
The ratio in eq.(29.46) is proportional to the current I. Using the values of the parameters specified in the problem we can calculate the ratio:
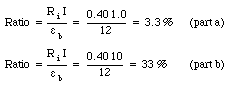
The current through the circuits discussed so far have been time-independent, as long as the emf of the source is time-independent. The currents in these circuits can be determined by applying Kirchhoff's first and/or second rule.
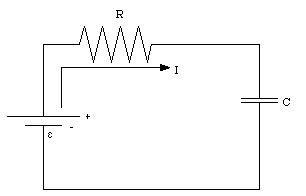
A simple circuit in which the current is time dependent is the RC circuit which consists of a resistor R connected in series with a capacitor C (see Figure 29.10). Applying Kirchhoff's second rule to the current loop I gives
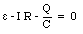
However, the current I through the resistor and the charge Q on the capacitor are related:
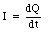
Substituting eq.(29.49) into eq.(29.48) we obtain
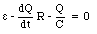
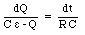
The second step is to integrate each side of eq.(29.51):
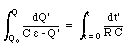
where Q0 is the charge on the capacitor at time t = 0. After evaluating both integrals in eq.(29.52) we obtain
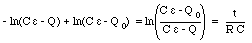
Equation (29.53) can be rewritten as
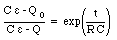
or
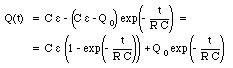
Let us consider the case in which the capacitor is discharged at time t = 0 (that is Q0 = 0 C). Equation (29.55) can then be rewritten as
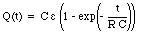
The charge on the capacitor will increase as function of time and the final charge Qf on the capacitor is equal to
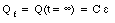
The time constant of the charging process of the capacitor is equal to RC. When the charged capacitor is connected in series across a resistor, the charge on the capacitor will decrease. The time constant for this process is also RC. Once we know the charge on the capacitor as function of time we can immediately find the current as function of time by applying eq.(29.48):
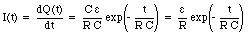
The current at time t = 0 is equal to [epsilon]/R and it decreases to zero with increasing time.