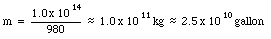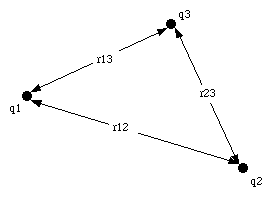

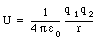
where q1 and q2 are the electric charges of the two objects, and r is their separation distance. The electric potential energy of a system of three point charges (see Figure 26.1) can be calculated in a similar manner
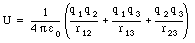
where q1, q2, and q3 are the electric charges of the three objects, and r12, r13, and r23 are their separation distances (see Figure 26.1). The potential energy in eq.(26.2) is the energy required to assemble the system of charges from an initial situation in which all charges are infinitely far apart. Equation (26.2) can be written in terms of the electrostatic potentials V:
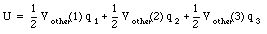
where Vother(1) is the electric potential at the position of charge 1 produced by all other charges
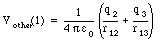
and similarly for Vother(2) and Vother(3).
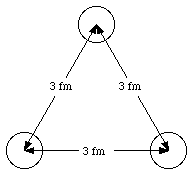
According to the alpha-particle model of the nucleus some nuclei consist of a regular geometric arrangement of alpha particles. For instance, the nucleus of 12C consists of three alpha particles on an equilateral triangle (see Figure 26.2). Assuming that the distance between pairs of alpha particles is 3 x 10-15 m, what is the electric energy of this arrangement of alpha particles ? Treat the alpha particles as pointlike.
The electric potential at the location of each alpha particle is equal to
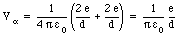
where d = 3.0 x 10-15 m. The electric energy of this configuration can be calculated by combining eq.(26.5) and eq.(26.3):
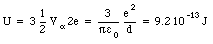
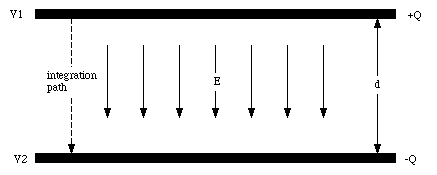
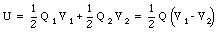
The electric field E between the plates is a function of the charge density [sigma]
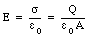
The potential difference V1 - V2 between the plates can be obtained by a path integration of the electric field
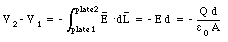
Combining eq.(26.9) and eq.(26.7) we can calculate the electrostatic energy of the system:
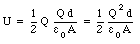
This equation shows that electrostatic energy can be stored in a capacitor. Equation (26.10) can be rewritten as
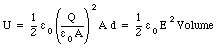
where Volume is the volume between the capacitor plates. The quantity [epsilon]0 . E2/2 is called the energy density (potential energy per unit volume).

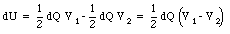
where V1 and V2 are the electrostatic potential of the top and bottom plate, respectively. The potential difference, V1 - V2, is related to the electric field between the plates
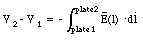
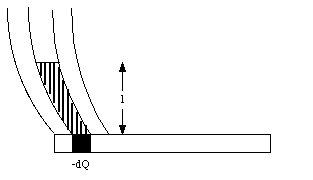
The electric field E(l) can be related to the charges on the small segments of the capacitor plates via Gauss' law. Consider a volume with its sides parallel to the field lines (see Figure 26.5). The electric flux through its surface is equal to
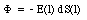
where E(l) is the strength of the electric field at a distance l from the bottom capacitor plate (see Figure 26.5) and dS(l) is the area of the top of the integration volume. The flux is negative since the field lines are entering the integration volume. The flux through the sides of the integration volume is zero since the sides are chosen to be parallel to the field lines. The flux through the bottom of the integration volume is also zero, since the electric field in any conductor is zero. Gauss' law requires that the flux through the surface of any volume is equal to the charge enclosed by that volume divided by [epsilon]0:
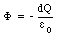
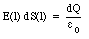
Equations (26.12), (26.13) and (26.16) can be combined to give
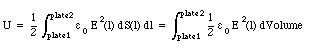
This calculation can be generalized to objects of arbitrary shapes, and the electrostatic energy of any system can be expressed as the volume integral of the energy density u which is defined as
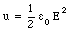
Thus
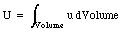
where the volume integration extends over all regions where there is an electric field.
In symmetric fission, the nucleus of uranium (238U) splits into two nuclei of palladium (119Pd). The uranium nucleus is spherical with a radius of 7.4 x 10-15 m. Assume that the two palladium nuclei adopt a spherical shape immediately after fission; at this instant, the configuration is as shown in Figure 26.6. The size of the nuclei in Figure 26.6 can be calculated from the size of the uranium nucleus because nuclear material maintains a constant density.
b) Calculate the total electric energy of the palladium nuclei in the configuration shown in Figure 26.6, immediately after fission. Take into account the mutual electric potential energy of the two nuclei and also the individual electric energy of the two palladium nuclei by themselves.
c) Calculate the total electric energy a long time after fission when the two palladium nuclei have moved apart by a very large distance.
d) Ultimately, how much electric energy is released into other forms of energy in the complete fission process ?
e) If 1 kg of uranium undergoes fission, how much electric energy is released ?
a) The electric energy of the uranium nucleus before fission can be calculated using the equations derived in Example 26.4 in Ohanian:
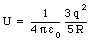
For the uranium nucleus q = 92e and R = 7.4 x 10-15 m. Substituting these values into eq.(26.20) we obtain
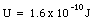
b) Suppose the radius of a palladium nucleus is RPd. The total volume of nuclear matter of the system shown in Figure 26.6 is equal to
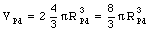
Since the density of nuclear matter is constant, the volume in eq.(26.22) must be equal to the volume of the original uranium nucleus
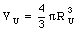
Combining eq.(26.23) and (26.22) we obtain the following equation for the radius of the palladium nucleus:
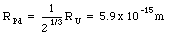
The electrostatic energy of each palladium nucleus is equal to
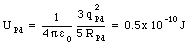
where we have used the radius calculated in eq.(26.24) and a charge qPd = 46e. Besides the internal energy of the palladium nuclei, the electric energy of the configuration must also be included in the calculation of the total electric potential energy of the nuclear system
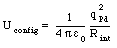
where qPd is the charge of the palladium nucleus (qPd = 26e) and Rint is the distance between the centers of the two nuclei (Rint = 2 RPd = 11.7 x 10-15 m). Substituting these values into eq.(26.26) we obtain
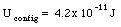
The total electric energy of the system at fission is therefore
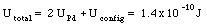
c) Due to the electric repulsion between the positively charge palladium nuclei, they will separate and move to infinity. At this point, the electric energy of the system is just the sum of the electric energies of the two palladium nuclei:
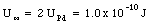
d) The total release of energy is equal to the difference in the electric energy of the system before fission (eq.(26.21)) and long after fission (eq.(26.29)):
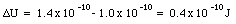
e) Equation (26.30) gives the energy released when 1 uranium nucleus fissions. The number of uranium nuclei in 1 kg of uranium is equal to
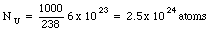
The total release of energy is equal to
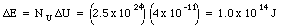
To get a feeling for the amount of energy released when uranium fissions, we can compare the energy in eq.(26.32) with the energy released by falling water. Suppose 1 kg of water falls 100 m. The energy released is equal to the change in the potential energy of the water:
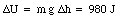
The mass of water needed to generate an amount of energy equal to that released in the fission of 1 kg uranium is