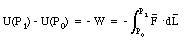
The electrostatic force is a conservative force. This means that the work it does on a particle depends only on the initial and final position of the particle, and not on the path followed. With each conservative force, a potential energy can be associated. The introduction of the potential energy is useful since it allows us to apply conservation of mechanical energy which simplifies the solution of a large number of problems.
The potential energy U associated with a conservative force F is defined in the following manner
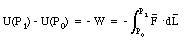
where U(P0) is the potential energy at the reference position P0 (usually U(P0) = 0) and the path integral is along any convenient path connecting P0 and P1. Since the force F is conservative, the integral in eq.(25.1) will not depend on the path chosen. If the work W is positive (force and displacement pointing in the same direction) the potential energy at P1 will be smaller than the potential energy at P0. If energy is conserved, a decrease in the potential energy will result in an increase of the kinetic energy. If the work W is negative (force and displacement pointing in opposite directions) the potential energy at P1 will be larger than the potential energy at P0. If energy is conserved, an increase in the potential energy will result in an decrease of the kinetic energy. If In electrostatic problems the reference point P0 is usually chosen to correspond to an infinite distance, and the potential energy at this reference point is taken to be equal to zero. Equation (25.1) can then be rewritten as:
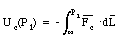
To describe the potential energy associated with a charge distribution the concept of the electrostatic potential V is introduced. The electrostatic potential V at a given position is defined as the potential energy of a test particle divided by the charge q of this object:
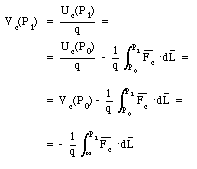
In the last step of eq.(25.3) we have assumed that the reference point P0 is taken at infinity, and that the electrostatic potential at that point is equal to 0. Since the force per unit charge is the electric field (see Chapter 23), eq. (25.3) can be rewritten as
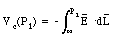
The unit of electrostatic potential is the volt (V), and 1 V = 1 J/C = 1 Nm/C. Equation (25.4) shows that as the unit of the electric field we can also use V/m.
A common used unit for the energy of a particle is the electron-volt (eV) which is defined as the change in kinetic energy of an electron that travels over a potential difference of 1 V. The electron-volt can be related to the Joule via eq.(25.3). Equation (25.3) shows that the change in energy of an electron when it crosses over a 1 V potential difference is equal to 1.6 . 10-19 J and we thus conclude that 1 eV = 1.6 . 10-19 J
A charge q is moved from P0 to P1 in the vicinity of charge q' (see Figure 25.1). The electrostatic potential at P1 can be determined using eq. (25.4) and evaluating the integral along the path shown in Figure 25.1. Along the circular part of the path the electric field and the displacement are perpendicular, and the change in the electrostatic potential will be zero. Equation (25.4) can therefore be rewritten as
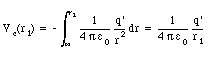
If the charge q' is positive, the potential increases with a decreasing distance r. The electric field points away from a positive charge, and we conclude that the electric field points from regions with a high electrostatic potential towards regions with a low electrostatic potential.
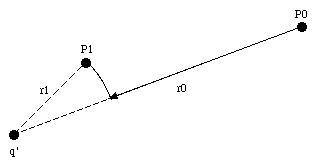
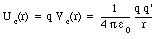
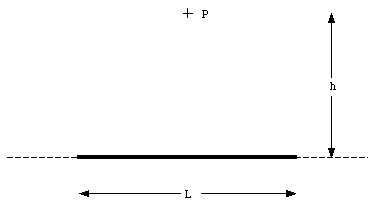
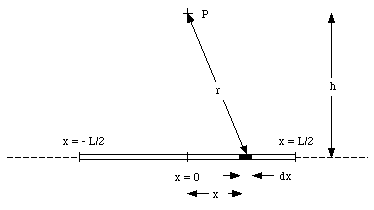
A total charge Q is distributed uniformly along a straight rod of length L. Find the potential at point P at a distance h from the midpoint of the rod (see Figure 25.2).
The potential at P due to a small segment of the rod, with length dx and charge dQ, located at the position indicated in Figure 25.3 is given by
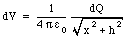
The charge dQ of the segment is related to the total charge Q and length L
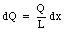
Combining equations (25.7) and (25.8) we obtain the following expression for dV:
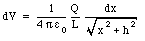
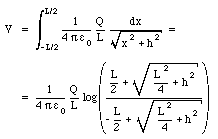
An alpha particle with a kinetic energy of 1.7 x 10-12 J is shot directly towards a platinum nucleus from a very large distance. What will be the distance of closest approach ? The electric charge of the alpha particle is 2e and that of the platinum nucleus is 78e. Treat the alpha particle and the nucleus as spherical charge distributions and disregard the motion of the nucleus.
The initial mechanical energy is equal to the kinetic energy of the alpha particle
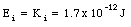
Due to the electric repulsion between the alpha particle and the platinum nucleus, the alpha particle will slow down. At the distance of closest approach the velocity of the alpha particle is zero, and thus its kinetic energy is equal to zero. The total mechanical energy at this point is equal to the potential energy of the system
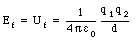
where q1 is the charge of the alpha particle, q2 is the charge of the platinum nucleus, and d is the distance of closest approach. Applying conservation of mechanical energy we obtain
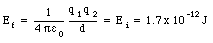
The distance of closest approach can be obtained from eq.(25.13)
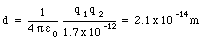
The electric field is a conservative field since the electric force is a conservative force. This implies that the path integral
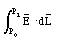
between point P0 and point P1 is independent of the path between these two points. In this case the path integral for any closed path will be zero:
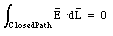
Equation (25.16) can be used to prove an interesting theorem:
" within a closed, empty cavity inside a homogeneous conductor, the electric field is exactly zero ".
The electrostatic potential V is related to the electrostatic field E. If the electric field E is known, the electrostatic potential V can be obtained using eq.(25.4), and vice-versa. In this section we will discuss how the electric field E can be obtained if the electrostatic potential is known.
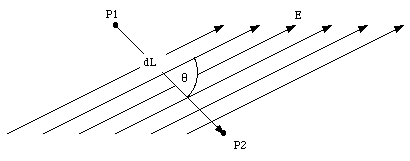
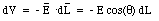
where the angle [theta] is the angle between the direction of the electric field and the direction of the displacement (see Figure 25.5). Equation (25.17) can be rewritten as
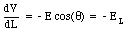
where EL indicates the component of the electric field along the L-axis. If the direction of the displacement is chosen to coincide with the x-axis, eq.(25.18) becomes
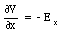
For the displacements along the y-axis and z-axis we obtain
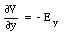
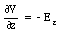
The total electric field E can be obtained from the electrostatic potential V by combining equations (25.19), (25.20), and (25.21):
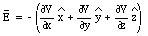
Equation (25.22) is usually written in the following form
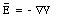
where --V is the gradient of the potential V.
In many electrostatic problems the electric field of a certain charge distribution must be evaluated. The calculation of the electric field can be carried out using two different methods:
1. the electric field can be calculated by applying Coulomb's law and vector addition of the contributions from all charges of the charge distribution.
2. the total electrostatic potential V can be obtained from the algebraic sum of the potential due to all charges that make up the charge distribution, and subsequently using eq.(25.23) to calculate the electric field E.
In many cases method 2 is simpler since the calculation of the electrostatic potential involves an algebraic sum, while method 1 relies on the vector sum.
In some region of space, the electrostatic potential is the following function of x, y, and z:
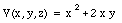
where the potential is measured in volts and the distances in meters. Find the electric field at the points x = 2 m, y = 2 m.
The x, y and z components of the electric field E can be obtained from the gradient of the potential V (eq.(25.23)):
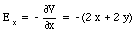
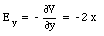
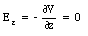
Evaluating equations (25.25), (25.26), and (25.27) at x = 2 m and y = 2 m gives
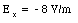
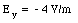
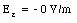
Thus
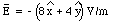
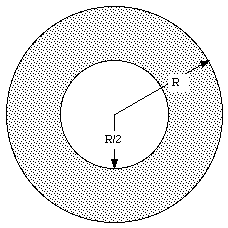
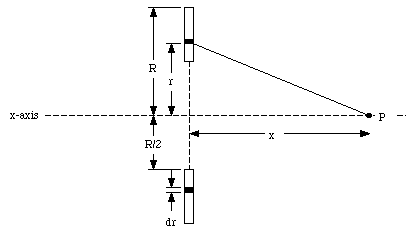
An annulus (a disk with a hole) made of paper has an outer radius R and an inner radius R/2 (see Figure 25.6). An amount Q of electric charge is uniformly distributed over the paper.
a) Find the potential as a function of the distance on the axis of the annulus.
b) Find the electric field on the axis of the annulus.
We define the x-axis to coincide with the axis of the annulus (see Figure 25.7). The first step in the calculation of the total electrostatic potential at point P due to the annulus is to calculate the electrostatic potential at P due to a small segment of the annulus. Consider a ring with radius r and width dr as shown in Figure 25.7. The electrostatic potential dV at P generated by this ring is given by
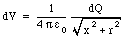
where dQ is the charge on the ring. The charge density [rho] of the annulus is equal to
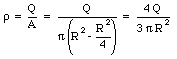
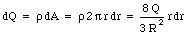
Substituting eq.(25.34) into eq.(25.32) we obtain
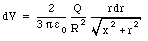
The total electrostatic potential can be obtained by integrating eq.(25.35) over the whole annulus:
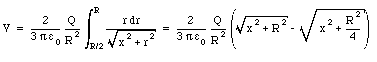
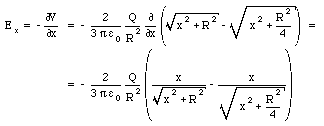
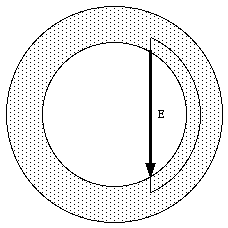
Since the electrostatic field and the electrostatic potential are related we can replace the field lines by so called equipotential surfaces. Equipotential surfaces are defined as surfaces on which each point has the same electrostatic potential. The component of the electric field parallel to this surface must be zero since the change in the potential between all points on this surface is equal to zero. This implies that the direction of the electric field is perpendicular to the equipotential surfaces.
Figure 25.8 shows an electric dipole located along the z-axis. It consists of two charges + Q and - Q, separated by a distance L. The electrostatic potential at point P can be found by summing the potentials generated by each of the two charges:
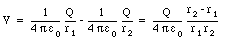
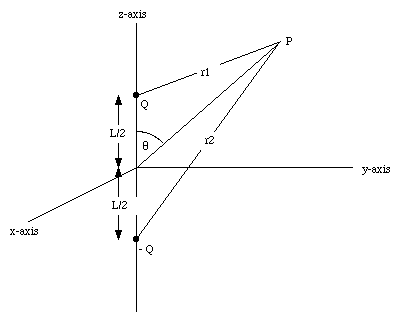
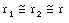
and
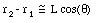
The electrostatic potential at P can now be rewritten as
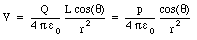
where p is the dipole moment of the charge distribution. The electric field of the dipole can be obtained from eq.(25.41) by taking the gradient (see eq.(25.23)).