Problem 1
When the coil is connected to the oscillator, it forms an RL circuit. The impedance of the RL circuit is equal to
![]()
The amplitude of the current is equal to
![]()
This equation can be rewritten as
![]()
or
![]()
Problem 2
We assume that the field produced by the solenoid is equal to that of a perfect solenoid. The field without a core is equal to
![]()
The magnetic field present with the core is equal to
![]()
The energy density is thus equal to
![]()
Problem 3
The magnetic field inside the solenoid is equal to
![]()
This equation can be used to determine the current that must be used to generate the magnetic field B:
![]()
Problem 4
Right after the battery is connected, the current in the circuit will be zero. The entire emf of the battery will thus be across the inductors. For conductor 1 we thus conclude that:
![]()
Problem 5.
Using the same procedure outline in Problem 4 we conclude that for conductor 2:
![]()
Problem 6
In a steady state, the current is constant (independent of time) and the potential drop across the inductors is thus equal to zero. This implies that the entire emf of the battery is across the resistor, and consequently the current through the resistor will be equal to
![]()
Problem 7
The parallel connection of the two inductors requires that they have the same potential difference across them. Thus:
![]()
This equation requires that
![]()
The sum of these current must be equal to the current through the resistor. Thus:
![]()
The current through inductor 1 is thus equal to
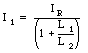
Problem 8
The current through inductor 2 is equal to
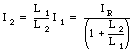
Problem 9
The impedance of the circuit is equal to
![]()
Problem 10
The impedance of the circuit is equal to
![]()
The amplitude of the current is equal to
![]()
Problem 11
Since all components are hooked up in series, the amplitude of the instantaneous current across the inductor will be the same as the amplitude of the instantaneous current across the capacitor. See solution for Problem 10.
Problem 12
The impedance of the LR circuit is equal to
![]()
The amplitude of the current is thus equal to
![]()
Problem 13
By using a phasor diagram (see for example Figure 34.18 in Ohanian) we can conclude that the phase angle [phi] can be determined from the following relation:
![]()
Thus
![]()
Problem 14
The power dissipated in the resistor is equal to
![]()
The current in the resistor is equal to
![]()
The average power dissipated in the resistor is equal to
![]()
Problem 15
NOTE: the graph for this problem can differ for different assignments. This solution is for the graph shown on the assignment of Frank Wolfs.
At time t1 the current has completed fT oscillations, where f = 1.75 for my graph. Thus:
![]()
The angular frequency of the generator is thus equal to
![]()
Problem 16
The current through the circuit element is equal to
![]()
The voltage across the circuit element is equal to
![]()
The power dissipated is in the circuit element at time t is equal to
![]()
The average power dissipated in the circuit element during one period is equal to zero.
Problem 17
Since the voltage and current are out of phase, the circuit elements is not a resistor. Since the current leads the voltage by 90deg., we conclude that the circuit elements must be a capacitor. The amplitude of the current in a circuit with a source of emf and a capacitor is equal to
![]()
The capacitance of the capacitor is thus equal to
![]()