Problem 1
The battery has a rating of x A-hr. This implies that it can deliver x A for 1 hour. 1 A is per definition equal to a 1.6 10-19 C/s. The total charge that moves through the battery is thus equal to
![]()
Problem 2
The total charge that flows through the battery crosses a potential difference of 12 V. The associated change in its potential energy is thus equal to
![]()
This is the total electrical energy that is delivered by the battery.
Problem 3
Assume that the total length of the telephone wire is L, and the short occurs at a distance x from C. The total length of cable between C and D is equal to 2 x. The resistance between C and D is thus equal to:
![]()
where r is the resistivity of the wire and A is its cross sectional area. The total length of cable between A and B is equal to 2 (L - x). The resistance between A and B is thus equal to
![]()
The ratio of the resistance is equal to
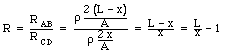
This equation can be used to determine x:
![]()
Problem 4
Use a coordinate system to describe the cone, which has the left-side of the cone located at x = 0 m. Consider a slice of the cone located a distance x from the origin, with thickness dx and radius r where
![]()
The resistance of this slice is equal to
![]()
The total resistance of the cone can be obtained by integrating x between x = 0 and x = h:
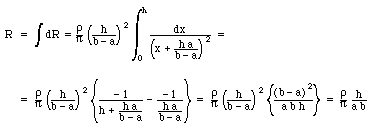
Note: since each of the slices is in series, the total resistance is just the sum of the resistance of each slice (thus the integral of dR)
Problem 5
NOTE: the following solution is correct for the circuit shown on the assignment of Frank Wolfs. Different diagrams might appear on different assignments, but the approach will be the same.
The net current at each branch must be zero. This immediately implies that:
![]()
or
![]()
Now consider the loop with resistors 1 and 2 (and go around this loop in a direction given by the current I2). Kirchhoffs' law states that the net emf around this loop must be equal to zero. Thus:
![]()
Do the same thing for the loop with resistors 2 and 3 (and go around this loop in a direction given by the current I2):
![]()
We now have two equations with two unknown. The current I1 is equal to
![]()
Problem 6
Consider the following three current loops, and assume that the current in each loop is flowing in a clockwise direction:
For loop 1 we require that:
![]()
This equation can be rewritten as
![]()
For loop 2 we require that
![]()
This equation can be rewritten as
![]()
For loop 3 we require that
![]()
A simple relation between the current through resistor 1 and the current through resistor 2 can be obtained by requiring that the potential difference across them is equal to the applied emf:
![]()
A second relation between these two currents between these two current can be found by multiplying the equation for loop 1 by -R4 and adding this to the equation for loop 2 multiplied by R5:
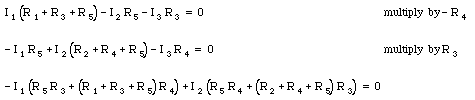
Combining the last two equations we can eliminate the current through resistor 2:
![]()
The current through resistor 1 is thus equal to
![]()
Problem 7
The current through resistor 2 is equal to
![]()
The current through resistor 5 is thus equal to
![]()
Therefore, the voltage across resistor 5 is equal to
![]()
Problem 8
NOTE: the following solution is correct for the circuit shown on the assignment of Frank Wolfs. Different diagrams might appear on different assignments, but the approach will be the same.
Consider the current loop from a to b to c to d to f to g and back to a. The sum of emfs and potential drops around this loop must be equal to 0 (Kirchhoffs' rule). Thus
![]()
This equation can be used to determine Vag:
![]()
Problem 9
NOTE: the following solution is correct for the circuit shown on the assignment of Frank Wolfs. Different diagrams might appear on different assignments, but the approach will be the same.
Consider the branch with resistors R2, R3, and R4. The net resistance of R3 and R4 in parallel is equal to:
![]()
The net resistance of R34 in series with R2 is equal to
![]()
The current through this chain is equal to
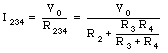
A fraction of this current is going through resistor R4. The relation between the current through R3 and the current through R4 is:
![]()
The fraction of the total current that goes through R3 is equal to:
![]()
Thus
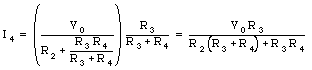
Problem 10
Consider two clockwise current loops; loop 1 with resistor R1 and emf source [epsilon]1, and loop 2 with resistor R2 and emf sources [epsilon]1 and [epsilon]2. For loop 1 we obtain according to Kirchhoff:
![]()
Thus
![]()
Problem 11
For loop 2 we obtain according to Kirchhoff:
![]()
Thus
![]()
Problem 12
The current going through emf e1 is equal to
![]()
The power delivered by emf e1 is thus equal to
![]()