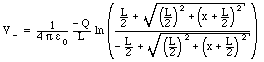
Problem 1
The total potential at P due to the charge distribution can be calculated by summing the potential at P due to each rod. The calculation of the potential at P due to the negatively charged rod is similar to the calculation for Problem 25.21 which was discussed in class (see lecture notes):
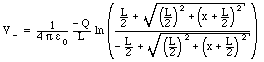
The potential at P due to the positively charged rod is equal to:
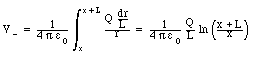
The total potential at P is thus equal to:
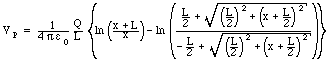
Problem 2
The total potential at P due to the charge distribution can be calculated by summing the potential at P due to each segment of the rod. In Problem 3 we will calculate the potential at the center of a semicircle. Using the result from problem 3 we can calculate the potential at P due to the two semicircles of radius R1 and R2:
![]()
The total potential at P due to the two straight sections of the charge configuration can be calculated using the result obtained in Problem 1:
![]()
The total electrostatic potential at P is the algebraic sum of the contributions of all segments and is equal to:
![]()
Problem 3
Consider a small segment of the semicircle. If this segment has a charge dQ, it will produce a potential dV at P where
![]()
The total potential at P is equal to the sum of the potentials dV generated by all the segments of the semicircle:
![]()
Problem 4
Consider a sphere of radius R and charge q. In the region outside the sphere it will generate an electric field that is that of a point charge q, located at the center of the sphere. The electrostatic potential in this region is thus also that of a point charge, and we thus conclude that the electrostatic potential at r =R is equal to
![]()
Assuming that sphere 1 has a charge q1 and a radius R1 we conclude that:
![]()
Assuming that sphere 2 has a charge q2 and a radius R2 we conclude that:
![]()
If the surfaces of the two spheres are maintained at the same potential we conclude that:
![]()
If the total charge on the system is Q than q1 + q2 = Q and
![]()
This can be rewritten as
![]()
or
![]()
Problem 5
The radial component of the electric field can be found by differentiating the electric potential with respect to r:
![]()
At r = R/2 the electric field is equal to:
![]()
Problem 6
The potential difference between (0,0,0) and (x1,y1,z1) can be found by integrating the electric field over the path connecting (0,0,0) and (x1,y1,z1). The path integral of the electric field is path independent, and we thus can choose the most convenient path for us to bring us from (0,0,0) to (x1,y1,z1). For example, we can go from (0,0,0) to (x1,0,0) to (x1,y1,0) to (x1,y1,z1). When we move from (0,0,0) to (x1,0,0) we move parallel to the x-axis, and consequently we only have to consider the x-component of the electric field which is zero since y = 0 along this part of the trajectory. When we move from (x1,0,0) to (x1,y1,0) we move parallel to the x-axis, and consequently we only have to consider the y-component of the electric field:
![]()
When we move from (x1,y1,0) to (x1,y1,z1) we move parallel to the z-axis, and consequently we only have to consider the z-component of the electric field which is zero. The total electric potential difference is thus equal to
![]()
Problem 7
The electrostatic potential energy of a pair of point charges (each of charge q) is equal to
![]()
In the current problem we are dealing with a large number of charge pairs:
The total electrostatic potential of the charge configuration is thus equal to
![]()
Problem 8
The graph shown in the problem must be used to determine dV/dx at the appropriate x position (make sure you notice that the vertical scale is in terms of kV and the horizontal scale in terms of m). The measured slope can be used to calculate the x-component of the electric field at the appropriate x position:
![]()
The x-component of the electric force acting on a charge q located at that position is thus equal to
![]()
Problem 9
The potential at 2 is equal to
![]()
The path integral only depends on the initial and the final point, and not on the actual path chosen. We thus can first move parallel to the x axis and then move parallel to the y axis in order to get from point 1 to point 2. When we move parallel to the y axis, the electric field is perpendicular to the path, and consequently the path integral along this section of the path is equal to 0. When we move parallel to the x axis, the field and the path are parallel and, since the field is uniform, the path integral along this section of the path is equal to the magnitude of the electric field times the length of the path. Thus:
![]()