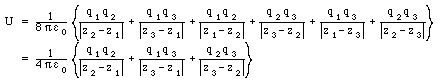---

Solutions Physics 122 Midterm Exam # 1

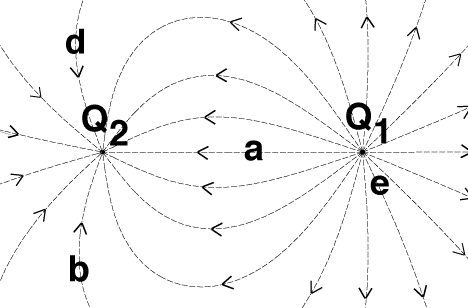
Figure Problem 1

Consider the Figure above which shows the electric field generated by two point charges. The following statements can be made in connection with the Figure:

• The direction of the electric field at a specific point is tangent to the field line. At 'b' the electric field is pointing straight up, and thus not directly towards Q2.
• The magnitude of the electric field is proportional to the density of field lines. Based on the given configuration of field lines, it is clear that the density of field lines at 'c' is not equal to zero, and thus the electric field at 'c' is not equal to zero.
• The density of field lines at 'a' is higher than the density of field lines at 'c'. Thus, the magnitude of the electric field at 'a' is larger that the magnitude of the electric field at 'c'.
• The line integral of the electric field along path between 'e' and 'c' is positive (electric field pointing in the same direction as the displacement). The change in the potential between 'e' and 'c' is equal to the opposite of the line integral of the electric field, and is thus negative. We thus conclude that the potential at 'c' is smaller than the potential at 'e'.
• The electric field at 'd' points straight down ('South').
• The number of field lines emerging from a positive charge is proportional to the magnitude of the positive charge. The number of field lines ending on a negative charge is proportional to the magnitude of the negative charge. There are 18 field lines emerging from the positive charge Q1 and 13 field lines ending on the negative charge Q2. This, |Q1| > |Q2| and Q1+Q2 > 0 C.

Problem 2

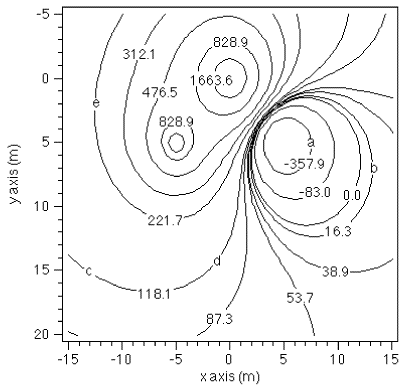
Figure Problem 2

• The electric field at any point is directed perpendicular to the equipotential contours. The electric field at 'e' will thus be directed perpendicular to the 221.7 V contour. The electric field will be directed from areas of higher potential to areas of lower potential. The direction at 'e' will thus be away from the 312.1 V contour.
• A charge released at rest on any of the contours shown will feel a non-zero electric force, and as a result will start to move. For a positive charge, the motion will be towards a region of lower potential; for a negative charge, the motion will be towards a region of higher potential.
• The potential at 'a' is -357.9 V. The potential at 'b' is 16.3 V, and is thus higher than the potential at 'a'.
• The potential in the vicinity of a positive charge will be positive. The potential in the vicinity of a negative charge will be negative. The diagram shown above indicates that there are two positive charges, and one negative charges.
• The potential at 'd' is 118.1 V. The potential at 'c' is also 118.1 V. There is thus no potential difference between 'd' and 'c', and as a consequence, no work is done when you move a charge from 'd' to 'c'. Note: you could also have concluded this by observing that the electric force is perpendicular to the trajectory while you move along a contour line, and thus the work done by this force is equal to 0 J.
• The 828.9 V contour line around the charge at (0,0) is located in closer proximity than the 828.9 V contour line around the charge at (-5,5). Since the potential depends on the q/r ratio close to a charge, a higher charge will produce the same potential at larger r. Thus, the charge at (0,0) is larger than the charge at (-5,5).

Problem 3

Consider an infinite rectangular box of height 2d as a Gaussian surface, and assume that the charge Q is located in the center of that box. Using Gauss' law we can conclude that the flux through this box is equal to

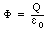
Due to the symmetry of the problem, half of the flux will go through the top infinite plane of the box, and half of it will go through the bottom infinite plane of the box. Thus the flux through each plane is equal to

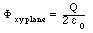
Problem 4

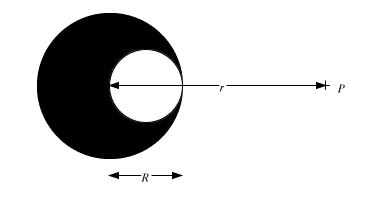
Figure Problem 4

This problem can be solved using the principle of superposition. Consider first a solid sphere of radius R and charge Q. The electric field generated by this charge distribution at point P is equal to

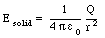
Now consider a second sphere with a charge density, identical in magnitude but of opposite sign, and a diameter R, located a distance R/2 from the center of the solid sphere. The electric field produced by this sphere at P is equal to

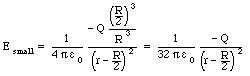
The superposition of these two charge distributions produces the charge distribution shown in this problem. The electric field generated by this charge distribution is thus the superposition of the electric fields generated by each of these two charge distributions separately.

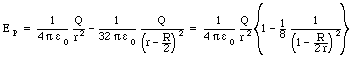
Problem 5

The electric fields inside the inner shell and outside the outer shells are equal to zero N/C. The electric field between the shells are that of a point charge Q (where Q is equal to the charge on the inner shell) located at the center of the shells:

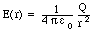
The corresponding energy density u(r) is equal to

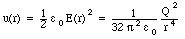
The total energy stored in the system can be obtained by integrating the energy density over the volume between the shells:

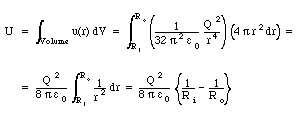
Problem 6

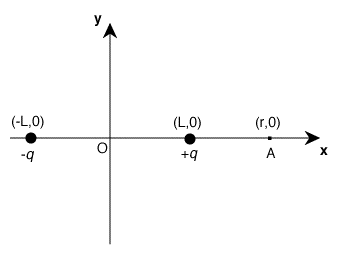
Figure Problem 6

The following conclusions can be drawn for electric field generated by the charge configuration shown in the Figure:

• The electric field at A due to the +q charge is directed towards the right. The electric field at A due to the -q charge is directed towards the left. However, since the magnitude of the electric field falls off as 1/r2, the magnitude of the field at A due to the +q charge will be larger than the magnitude of the field at A due to the -q charge. The net field at A will therefore be directed towards the right.
  
• The electric fields at the origin due each of the charges is pointed towards the left. At A, the two components are directed in opposite directions, and in addition, the component due to the -q charge is significantly smaller (due to the 1/r2 dependence of the electric field). The magnitude of the net electric field at A will thus be smaller than the magnitude of the electric field at the origin.
  
• The direction of the electric field on the negative y-axis is directed towards the left. At any point on the negative y-axis, the magnitude of the components due to the +q and the -q charges will be equal. The direction of these components is such that their vertical components cancel, and the net field is directed parallel to the x-axis, towards the left.
  
• The electric field at (-r,0) due to the -q charge is directed towards the right. The electric field at (-r,0) due to the +q charge is directed towards the left. However, since the magnitude of the electric field falls off as 1/r2, the magnitude of the field at (-r,0) due to the -q charge will be larger than the magnitude of the field at (-r,0) due to the +q charge. The net field at (-r,0) will therefore be directed towards the right.
  
• The direction of the electric field on the positive y-axis is directed towards the left. At any point on the positive y-axis, the magnitude of the components due to the +q and the -q charges will be equal. The direction of these components is such that their vertical components cancel, and the net field is directed parallel to the x-axis, towards the left.
  
• The electric fields at the origin due each of the charges is pointed towards the left. The net electric field at the origin is thus also pointed towards the left.

Problem 7

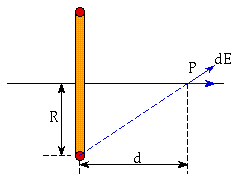
Figure Problem 7

Due to the symmetry of the problem we can immediately conclude that the net electric field on the axis of the ring is directed along this axis (see Figure). Consider a small segment of the ring with charge dQ. The electric field generate on the axis of the ring by this charge dQ is equal to

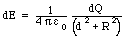
The component of the field directed along the axis of the ring is equal to

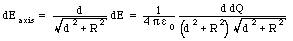
The total electric field due to the entire ring is thus equal to

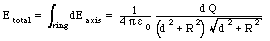
The problem specifies the charge density of the ring. Using the specified density we conclude that

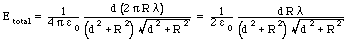
Problem 8

We can calculate the potential energy of the system most easily by using the following equation:

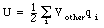
The potential at z1 due to the other two charges is equal to

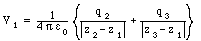
The potential at z2 due to the other two charges is equal to

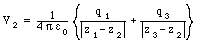
The potential at z3 due to the other two charges is equal to

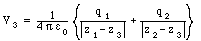
The total potential energy of the system is thus equal to
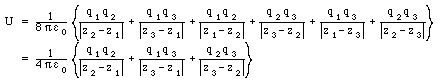
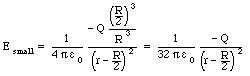
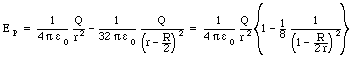
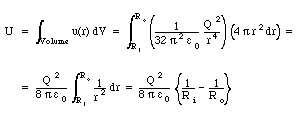
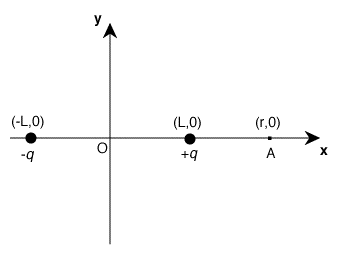