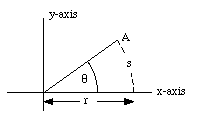
In this chapter we will be dealing with the rotation of a rigid body about a fixed axis. Every point of the body moves in a circle, whose center lies on the axis of rotation, and every point experiences the same angular displacement during a particular time interval.
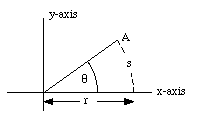
Figure 11.1. Relation between s and [theta].
Suppose the z-axis of our coordinate system coincides with the axis of rotation of the rigid body. The x-axis and the y-axis are taken to be perpendicular to the z-axis. Each part of the rigid body moves in a circle around the z-axis. Suppose a given point A on the body covers a linear distance s during the rotation (see Figure 11.1). During one complete revolution point A covers a distance equal to 2[pi]r. In that case, the angle of rotation is equal to 2[pi] radians. For the situation shown in Figure 11.1, the angle of rotation can be easily calculated:
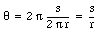
In describing the rotation of a rigid body we have to choose a reference line with respect to which the angle of rotation is being measured. In figure 11.1 the reference line connects the origin of the coordinate system and point A. The angle of rotation is the angle between the reference line and the x-axis (as is shown in Figure 11.1).
If the angle of rotation [theta] is time dependent, it makes sense to introduce the concept of angular velocity and angular acceleration. The angular velocity [omega] is defined as
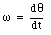
The unit of the angular velocity is rad/s. The angular velocity can be positive (counterclockwise rotation) or negative (clockwise rotation). The angular acceleration a is defined as
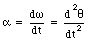
The unit of the angular acceleration is rad/s2.
In order to describe rotation around a point (rather than a fixed axis) the concept of an angular velocity vector is introduced. The magnitude of the angular velocity vector is equal to the absolute value of the angular velocity for rotation around a fixed axis (as defined above). The direction of the velocity vector is parallel to the rotation axis and the right-hand rule needs to be used to determine whether the vector points upwards or downwards.
Problem 7P
A wheel rotates with an angular acceleration a given by
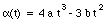
where t is the time and a and b are constants. If the wheel has an initial angular velocity [omega]0, write the equations for (a) the angular velocity and (b) the angle turned as function of time.
To solve this problem, we start with looking at the relation between the angular acceleration and the angular velocity
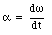
This relation can be rewritten as
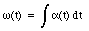
Substituting the given angular acceleration we obtain for the angular velocity
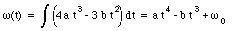
The angle of rotation is related to the angular velocity
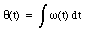
Substituting the derived expression for [omega](t) the angle of rotation can be calculated
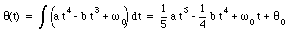
and therefore
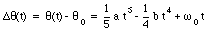
If the angular acceleration a is constant (time independent) the following equations can be used to calculate [omega] and [theta] at any time t:
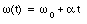
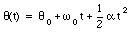
Note that these equations are very similar to the equations for linear motion.
Problem 19P
A wheel starting from rest, rotates with a constant angular acceleration of 2.0 rad/s2. During a certain 3.0 s interval it turns through 90 rad. (a) How long had the wheel been turning before the start of the 3.0 s interval ? (b). What was the angular velocity of the wheel at the start of the 3.0 s interval ?
Time t = 0 s is defined as the moment at which the wheel is at rest. Therefore, [omega]0 = 0 rad/s. The rotation angle at any later time is measured with respect to the position of the body at time t = 0 s: [theta]0 = 0 rad. The equations of rotation are now given by
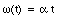
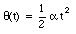
The angle of rotation during a 3.0 s interval will depend on time:
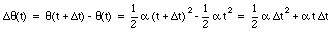
In our problem, the rotation [Delta][theta] during a period [Delta]t is given. The time that the wheel has been turning before the time period [Delta]t can be easily calculated
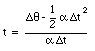
The angular velocity of the wheel at the beginning of this period is
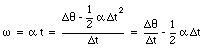
An example of the relation between angular and linear variables has already been discussed. Figure 1 illustrates how the distance s, covered by point A, is related to the radius of the circle and the angle of rotation
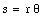
The velocity of point A can be obtained by differentiating this equation with respect to time
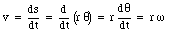
To derive this equation we have assumed that for rotations around a fixed axis the distance r from point A to the rotation axis is constant (independent of time) which is true for a rigid body. The acceleration of point A can be determined as follows
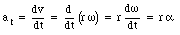
The acceleration at is the tangential component of the linear acceleration, related to the change in the magnitude of the velocity of point A. However, we have seen that an object carrying out a circular motion also experiences a radial acceleration. The magnitude of the radial component, ar, is
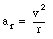
Using the previously derived expression for v in terms of [omega] and r, we can rewrite the radial component of the acceleration as follows
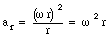
Figure 11.2 shows the direction of both the radial and the tangential components of the acceleration of point A. The radial component is always present as long as [omega] is not equal to zero; the tangential component is only present if the angular acceleration is not zero.
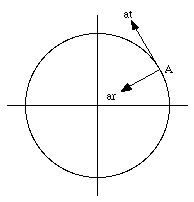
Figure 11.2. Components of the acceleration of point A.
We can conclude that when a rigid body is rotating around a fixed axis, every part of the body has the same angular velocity [omega] and the same angular acceleration a, but points that are located at different distances from the rotation axis have different linear velocities and different linear accelerations.
The total kinetic energy of a rotating object can be found by summing the kinetic energy of each individual particle:
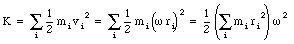
To derive this equation we have used the fact that the angular velocity is the same for each particle of the rigid body. The quantity in parenthesis tells us how the mass of the rotating body is distributed around the axis of rotation. This quantity is called the moment of inertia (or rotational inertia)
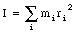
The unit for I is kg m2. Using this definition, we can write the kinetic energy of the rotating object as
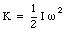
Note: in many previous problems we have assumed to be dealing with massless pulleys. This assumption assures that by applying conservation of mechanical energy we do not have to consider the kinetic energy related to the rotation of the pulley.
To calculate the moment of inertia of a rigid body we have to integrate over the whole body
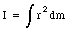
If the moment of inertia about an axis that passes through the center of mass is known, the moment of inertia about any other axis, parallel to it, can be found by applying the parallel-axis theorem
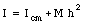
where Icm is the moment of inertia about an axis passing through the center of mass, M is the total mass of the body, and h is the perpendicular distance between the two parallel axes.
Sample Problem 11-8
Determine the moment of inertia of a uniform rod of mass m and length L about an axis at right angle with the rod, though its center of mass (see Figure 11.3).
The mass per unit length of the rod is m/L. The mass dm of an element of the rod with length dx is
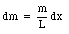
The contribution of this mass to the total moment of inertia of the rod is
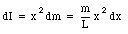
The total moment of inertia of the rod can be determined by integrating over all parts of the rod:
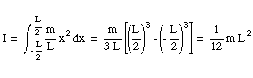
The moment of inertia of the rod around its end point (see Figure 11.4) can now be calculated using the parallel axes theorem
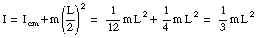
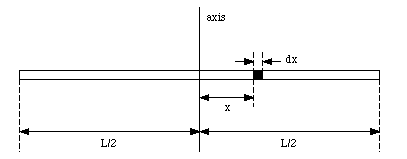
Figure 11.3. Sample Problem 11-8.
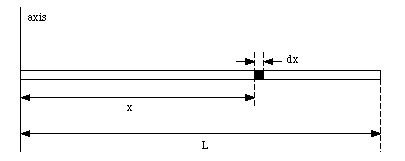
Figure 11.4. Sample Problem 11.8.
Example: Moment of Inertia of Disk
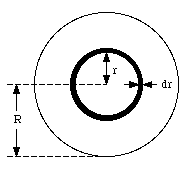
Figure 11.5. Moment of inertia of a disk.
A uniform disk has a radius R and a total mass M. The density of the disk is given by
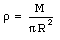
To calculate the moment of inertia of the whole disk, we first look at a small section of the disk (see Figure 5). The area of the ring located at a distance r from the center and having a width dr is
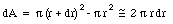
The mass of this ring is
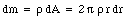
The contribution of this ring to the total moment of inertia of the disk is given by
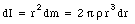
The total moment of inertia can now be found by summing over all rings:
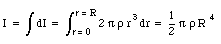
Substituting the calculated density we obtain
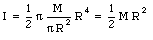
Suppose a force F is applied to point A (see Figure 11.6). Point A is part of a rigid body with an axis of rotation going through the origin. Suppose the angle between the force F and the position vector r is [phi]. The force F can be decomposed into two components: one parallel to the position vector and one perpendicular to the position vector. It is obvious that the component parallel to the position vector can not cause a rotation of the rigid body.
The magnitude of the component of the force perpendicular to the position vector is given by
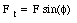
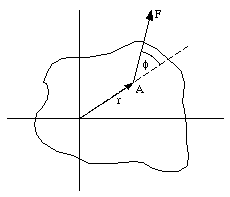
Figure 11.6. Torque
The tangential component of the applied force F will produce a rotation of the object; the actual angular velocity will depend not only on the applied force but also on the distance between the axis of rotation and point A. To describe the effect of the force, the concept of torque is introduced.
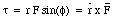
The tangential component of F, Ft, will produce a tangential acceleration a t
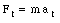
The torque [tau] can be rewritten as
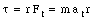
The tangential acceleration at is related to the angular acceleration a
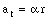
We conclude that
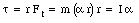
This is just Newton's second law for rotation.
Sample Problem 11-11
Figure 11.7 shows a uniform disk with mass M and radius R. The disk is mounted on a fixed axle. A block with mass m hangs from a light cord that is wrapped around the rim of the disk. Find the acceleration of the falling block, the angular acceleration of the disk, and the tension of the cord.
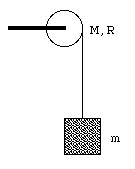
Figure 11.7. Sample Problem 11-10.
The forces acting on the mass and the disk are shown in Figure 11.8. Since the mass m is moving downward, the gravitational force m . g must exceed the tension T in the cord. The linear acceleration of the mass m is defined to be positive if it points down:
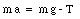
The uniform disk rotates as a result of the presence of mass m. The torque exerted by the tension T of the cord on the disk is
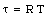
The resulting angular acceleration a of the disk can be obtained from the torque
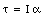
or
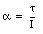
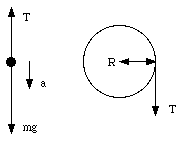
Figure 11.8. Sample Problem 11-10.
The moment of inertia of the disk is given by
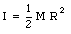
The angular acceleration a is equal to
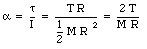
However, the linear acceleration of the cord is a, and therefore the linear acceleration of the rim of the disk must also be a. The linear acceleration of the rim and the angular acceleration a are related as follows
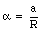
Combining this expression with the previous expression we can conclude that
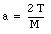
If we combine this expression with a previously derived expression for a
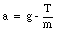
we can calculate a and T:
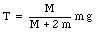
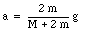
We see that the acceleration of the falling block is always less than the gravitational acceleration, but approaches g when the mass of the disk becomes much smaller than the mass m. The angular acceleration a can be obtained from
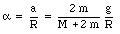
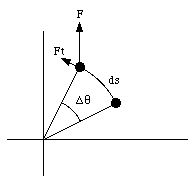
Figure 11.9. Work done by a force.
Suppose a particle with mass m is connected to the end of a rod (with negligible mass). Under the influence of a force F, the system rotates through an angle [Delta][theta] (see Figure 11.9). The work done by the force F is determined by the tangential component of F
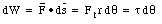
Here r d[theta] is the length of the arc traversed by the particle. The total work done by the force during a finite rotation (from [theta]i to [theta]f) is given by
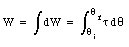
This equation is very similar to what we have derived for linear motion:
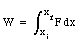
The total work done can now be calculated
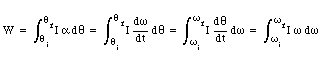
or
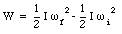
This can be rewritten as
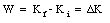
This relation shows that the work done by the torque acting on a rigid body is equal to the change in rotational kinetic energy of that body.