18. The Kinetic Theory of Gases

18.1. Avogadro constant

The laws of classical thermodynamics do not show the direct dependence of the observed macroscopic variables on microscopic aspects of the motion of atoms and molecules. It is however clear that the pressure exerted by a gas is related to the linear momentum of the atoms and molecules, and that the temperature of the gas is related to the kinetic energy of the atoms and molecules. In relating the effects of the motion of atoms and molecules to macroscopic observables like pressure and temperature, we have to determine the number of molecules in the gas. The mole is a measure of the number of molecules in a sample, and it is defined as

" the amount of any substance that contains as many atoms/molecules as there are atoms in

a 12-g sample of 12C "

Laboratory experiments show that the number of atoms in a 12-g sample of 12C is equal to 6.02 x 1023 mol-1. This number is called the Avogadro constant, NA. The number of moles in a sample, n, can be determined easily:

18.2. The Ideal Gas

Avogadro made the suggestion that all gases - under the same conditions of temperature and pressure - contain the same number of molecules. Reversely, if we take 1 mole samples of various gases, confine them in boxes of identical volume and hold them at the same temperature, we find that their measured pressures are nearly identical. Experiments showed that the gases obey the following relation (the ideal gas law):

where n is the number of moles of gas, and R is the gas constant. R has the same value for all gases:

The temperature of the gas must always be expressed in absolute units (Kelvin).

Using the ideal gas law we can calculate the work done by an ideal gas. Suppose a sample of n moles of an ideal gas is confined in an initial volume Vi. The gas expands by moving a piston. Its final volume is Vf. During the expansion the temperature T of the gas is kept constant (this process is called isothermal expansion). The work done by the expanding gas is given by

The ideal gas law provides us with a relation between the pressure and the volume

Since T is kept constant, the work done can be calculated easily

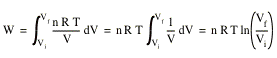
Note:

Sample Problem 18-1

A cylinder contains oxygen at 20°C and a pressure of 15 atm. at a volume of 12 l. The temperature is raised to 35°C , and the volume is reduced to 8.5 l. What is the final pressure of the gas ?

The ideal gas law tells us that

The initial state of the gas is specified by Vi, pi and Ti; the final state of the gas is specified by Vf, pf and Tf. We conclude that

Thus

The temperature T in this formula must be expressed in Kelvin:

Ti = 293 K

Tf = 308 K

The units for the volume and pressure can be left in l and atm. since only their ratio enter the equation. We conclude that pf = 22 atm.

18.3. Pressure and Temperature: A Molecular View

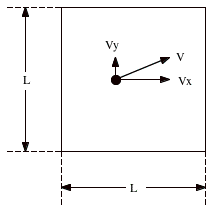
Let n moles of an ideal gas be confined to a cubical box of volume V. The molecules in the box move in all directions with varying speeds, colliding with each other and with the walls of the box. Figure 18.1 shows a molecule moving in the box. The molecule will collide with the right wall. The result of the collision is a reversal of the direction of the x-component of the momentum of the molecule:

Figure 18.1. Molecule moving in box.

The y and z components of the momentum of the molecule are left unchanged. The change in the momentum of the particle is therefore

After the molecule is scattered of the right wall, it will collide with the left wall, and finally return to the right wall. The time required to complete this path is given by

Each time the molecule collides with the right wall, it will change the momentum of the wall by ∆p. The force exerted on the wall by this molecule can be calculated easily

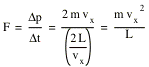
For n moles of gas, the corresponding force is equal to

The pressure exerted by the gas is equal to the force per unit area, and therefore

The term in parenthesis can be rewritten in terms of the average square velocity:

Thus, we conclude that

where M is the molecular weight of the gas. For every molecule the total velocity can be calculated easily

Since there are many molecules and since there is no preferred direction, the average square of the velocities in the x, y and z-direction are equal

and thus

Using this relation, the expression for the pressure p can be rewritten as

where vrms is called the root-mean-square speed of the molecule. The ideal gas law tells us that

Combining the last two equations we conclude that

and

For H at 300 K vrms = 1920 m/s; for 14N vrms = 517 m/s. The speed of sound in these two gases is 1350 m/s and 350 m/s, respectively. The speed of sound in a gas will always be less than vrms since the sound propagates through the gas by disturbing the motion of the molecules. The disturbance is passed on from molecule to molecule by means of collisions; a sound wave can therefore never travel faster than the average speed of the molecules.

18.4. Translational Kinetic Energy

The average translational kinetic energy of the molecule discussed in the previous section is given by

Using the previously derived expression for vrms, we obtain

The constant k is called the Boltzmann constant and is equal to the ratio of the gas constant R and the Avogadro constant NA

The calculation shows that for a given temperature, all gas molecules - no matter what their mass - have the same average translational kinetic energy, namely (3/2)kT. When we measure the temperature of a gas, we are measuring the average translational kinetic energy of its molecules.

18.5. Mean Free Path

The motion of a molecule in a gas is complicated. Besides colliding with the walls of the confinement vessel, the molecules collide with each other. A useful parameter to describe this motion is the mean free path l. The mean free path l is the average distance traversed by a molecule between collisions. The mean free path of a molecule is related to its size; the larger its size the shorter its mean free path.

Suppose the gas molecules are spherical and have a diameter d. Two gas molecules will collide if their centers are separated by less than 2d. Suppose the average time between collisions is ∆t. During this time, the molecule travels a distance v . ∆t, and sweeps a volume equal to

If on average it experiences one collision, the number of molecules in the volume V must be 1. If N is the number of molecules per unit volume, this means that

The time interval ∆t defined in this manner is the mean time between collisions, and the mean free path l is given by

Here we have assumed that only one molecule is moving while all others are stationary. If we carry out the calculation correctly (all molecules moving), the following relation is obtained for the mean free path:

The relation derived between the macroscopic pressure and the microscopic aspects of molecular motion only depend on the average root-mean-square velocity of the molecules in the gas. Quit often we want more information than just the average root-mean-square velocity. For example, questions like what fraction of the molecules have a velocity larger than v0 can be important (nuclear reaction cross sections increase dramatically with increasing velocity). It can be shown that the distribution of velocities of molecules in as gas is described by the so-called Maxwell velocity distribution

The product P(v)dv is the fraction of molecules whose speed lies in the range v to v + dv. The distribution is normalized, which means that

The most probable speed, vp, is that velocity at which the speed distribution peaks. The most probable speed is obtained by requiring that dP/dv = 0

We conclude that dP/dv = 0 when

and thus

The average speed of the gas molecules can be calculated as follows

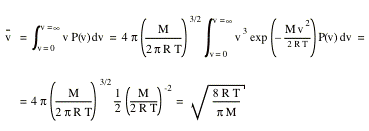
The mean square speed of the molecules can be obtained in a similar manner.

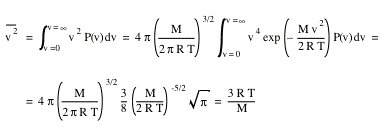
The root-mean-square speed, vrms, can now be obtained

We observe that vp < vav < vrms.

18.6. Heat Capacity of Ideal Gas

The internal energy of a gas is related to the kinetic energy of its molecules. Assume for the moment that we are dealing with a monatomic gas. In this case, the average translational kinetic energy of each gas molecule is simply equal to 3kT/2. If the sample contains n moles of such a gas, it contains nNA molecules. The total internal energy of the gas is equal to

We observe that the total internal energy of a gas is a function of only the gas temperature, and is independent of other variables such as the pressure and the density. For more complex molecules (diatomic N2 etc.) the situation is complicated by the fact that the kinetic energy of the molecules will consist not only out of translational motion, but also out of rotational motion.

18.6.1. Molar Heat Capacity at Constant Volume

Suppose we heat up n moles of gas while keeping its volume constant. The result of adding heat to the system is an increase of its temperature

Here, CV is the molar heat capacity at constant volume, ∆Q is the heat added, and ∆T is the resulting increase in the temperature of the system. The first law of thermodynamics shows that

Since the volume is kept constant (∆V = 0) we conclude that

and

Using the previously derived equation for U in terms of T we can show that

and thus

18.6.2. Molar heat Capacity at Constant Pressure

Suppose that, while heat is added to the system, the volume is changed such that the gas pressure does not change. Again, the change in the internal energy of the system is given by

where Cp is the molar heat capacity at constant pressure. This expression can be rewritten as

For an ideal gas (pV = nRT) we can relate ∆V to ∆T, if we assume a constant pressure

Using this relation, the first law of thermodynamics can be rewritten as

However, the internal energy U depends only on the temperature and not on how the volume and/or pressure is changing. Thus, ∆U/∆T = 3/2 n R = n CV. The previous equation can therefore be rewritten as

We see that Cp ≠ CV.

18.7. The Adiabatic Expansion of an Ideal Gas

During an adiabatic expansion of an ideal gas no heat is added or extracted from the system. This can be achieved by either expanding the gas very quickly (such that there is not time for the heat to flow) or by very well insulating the system. The first law of thermodynamics tells us that