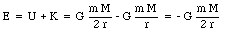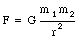
Gravity is the weakest force we know, but it is the force of gravity that controls the evolution of the universe. Every body in the universe attracts every other body. Newton proposed that the magnitude of this force is given by
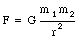
where m1 and m2 are the masses of the particles, r is the distance between them and G is a universal constant whose value is
G = 6.67 x 10-11 N m2/kg2
The gravitational forces between two particles act along the line joining them, and form an action-reaction pair (see Figure 14.1).
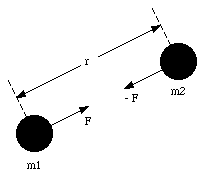
Figure 14.1. The gravitational force.
In real life we are not dealing with point particles; instead we are dealing with extended objects. To evaluate the gravitational force between extended objects, the shell theorem can be used:
"A uniform shell of matter attracts an external particle as if all the shell's mass were concentrated at its center"
Proof:
Figure 14.2 shows a shell located a distance r from a particle with mass m. The radius of the shell is R and its mass is M. The mass density of the shell is given by
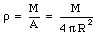
All points on the small hoop indicated in Figure 14.2 have the same distance to the particle m. The magnitude of the gravitational attraction between any of these points and the mass m is therefore the same. The net force between the hoop and mass m acts along the axis connecting the center of the shell and mass m. The area of the hoop is given by
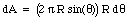
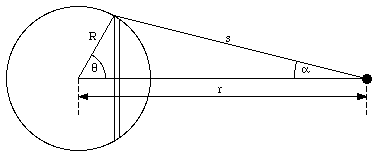
Figure 14.2. Shell theorem.
and its mass m is equal to
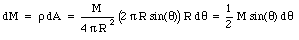
The net force is equal to
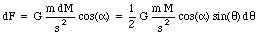
The angles [theta] and a can be eliminated by using the following relations:
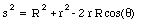
and
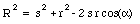
Differentiating the first of these two equations with respect to [theta] we obtain
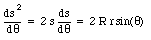
or
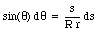
Further more we see that
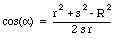
The total force acting on mass m can now be obtained easily
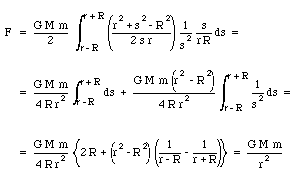
The shell theorem immediately shows that a sphere of uniform density (and mass M) attracts an external particle as if all the mass of the sphere is concentrated in its center.
In a similar fashion we can proof that a uniform shell of matter exerts no gravitational force on a particle located inside it .
The strength of the gravitational force depends on the value of G. The value of the gravitational constant can be determined using the Cavendish apparatus. Two small lead spheres of mass m are connected to the end of a rod of length L which is suspended from it midpoint by a fine fiber, forming a torsion balance. Two large lead spheres, each of mass M, are placed in the location indicated in Figure 14.3. The lead spheres will attract each other, exerting a torque on the rod. In the equilibrium position the gravitational torque is just balanced by the torque exerted by the twisted fiber. The torque exerted by the twisted wire is given by
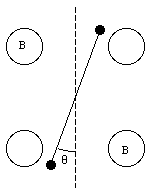
Figure 14.3. The Cavendish Apparatus.
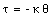
The torque exerted by the gravitational force is given by
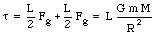
where R is the equilibrium distance between the center of the large and the small spheres. If the system is in equilibrium, the net torque acting on the rod is zero. Thus
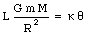
All of a sudden the large spheres are rotated to a new position (position B in Figure 14.3). The net torque acting on the twisted fiber is now not equal to zero, and the system will start to oscillate. The period of oscillation is related to the rotational inertia and the torsion constant [kappa]
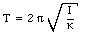
The angle between the two equilibrium positions is measured to be 2[theta]. This, combined with the measured torsion constant, is sufficient to determine the torque [tau] acting on the torsion balance due to the gravitational force. Measurements show that G = 6.67 x 10-11 Nm2/kg2.
If the mass density of the earth depends only on the distance from the center of the earth (homogeneous shells), we can easily calculate the net gravitational force acting on a particle of mass m, located at an external point, a distance r from the center of the earth:
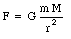
where M is the mass of the earth. For a particle on the earth surface, r = Re, the gravitational force is given by
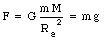
We conclude that the free-fall acceleration depends on the mass of the earth and its radius:
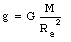
The measured value of g = 9.8 m/s2 and Re = 6.37 x 106 m gives
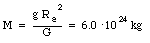
which is in good agreement with the accepted value of 5.98 x 1024 kg. In reality, the situation is more complicated:
To illustrate the effect of the rotation of the earth on the gravitational acceleration, consider a mass m located on a scale at the equator (see Figure 14.4). The mass m will carry out a uniform circular motion with a period T equal to 24 hours. The radius of the circle is equal to the radius of the earth Re. The corresponding centripetal acceleration is given by
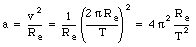
The following forces act on the mass:
1. The gravitational force m g0 (downwards)
2. The force W exerted by the scale on the mass (upwards)
The net force acting on the mass must be equal to the centripetal force required for the circular motion:
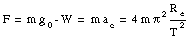
Figure 14.4. Mass located at equator.
The effective free-fall acceleration, obtained from the measured weight W, is given by
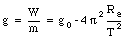
For the earth,
g0 - g = 0.034 m/s2
In chapter 8 we have discussed the relation between the force and the potential energy. Consider two particles of masses m1 and m2, separated by a distance r. In the gravitational field it is convenient to define the zero potential energy configuration to be one in which the two particles are separated by a large distance (infinity). Suppose the two masses are brought together (distance r) from infinity, along the path connecting the centers of the two masses. The work done by the gravitational force can be calculated as follows
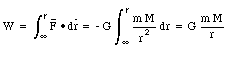
(note that the force F and the position vector r are pointed in an opposite direction, and the angle between them is 180deg.). The potential energy U(r) is now given by
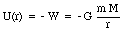
The potential energy is always negative and is a property of the two masses together rather than of either mass alone. We can verify our calculation by using U(r) to calculate the gravitational force
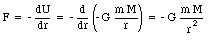
which is of course equal to Newton's law of gravity.
The work done by the gravitational force depends only on its initial and its final position, and not on the actual path followed. For example, a baseball travels from point A to point B (see Figure 14.5). The work done by the gravitational force on the baseball along the arcs is zero since the force and displacement are perpendicular. The only segments that contribute to the work done are those segments along the radial direction. The work done is negative if the force and the displacement are pointing in the opposite direction; if the force and the displacement are pointing in the same direction the work is positive Therefore the net work done if we travel along the radial direction back-and-forth (initial and final points coincide) is zero. We can now easily show that the net work done by the gravitational force on the baseball is just determined by its initial radial position and its final radial position.
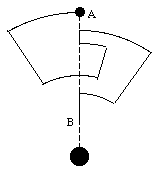
Figure 14.5. Work done by the gravitational force.
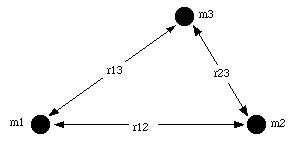
Figure 14.6. A system of three particles.
If the system contains more than two particles, the principle of superposition applies. In this case we consider each pair and the total potential energy is equal to the sum of the potential energies of each pair. This is illustrated in Figure 14.6 for a system consisting of 3 particles. In calculating the total potential energy of a system of particles one should take great care not to double count the interactions. The total potential energy of the system shown in Figure 14.6 can be easily calculated:
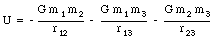
The total potential energy of a system of particles is sometimes called the binding energy of the system. The total potential energy is the amount of work that needs to be done to separate the individual parts of the system and bring them to infinity.
Example
The gravitational potential can be used to calculate the minimum initial speed that a projectile must have to escape from the earth. Suppose a projectile of mass m has a speed v. Its initial kinetic energy if given by
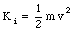
The initial potential energy of the projectile is given by
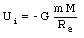
and its initial mechanical energy is equal to
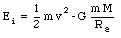
In deep space the potential energy of the projectile will be zero, and its minimum kinetic energy will also be equal to zero. We conclude that the minimum mechanical energy of the projectile must be zero. Therefore
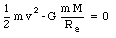
and
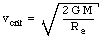
This initial speed is called the escape speed. For the earth we obtain
vcrit = 1.1 x 104 m/s
Suppose a planet with mass m is in a circular orbit around the sun, whose mass is M. The radius of the orbit is r. The gravitational force between the sun and the planet is given by
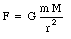
This is the force that keeps the planet in its circular orbit and its magnitude should therefore be equal to the centripetal force FC:
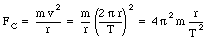
This implies that
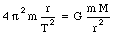
or
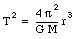
This shows that for circular orbits, the square of the period of any planet is proportional to the cube of the radius of the orbit (law of periods). The constant depends only on the mass of the sun (M) and the gravitational constant (G).
In reality none of the planets carry out a circular orbit; their orbits are elliptical. The general equation of an ellipse is given by (see Figure 14.7)
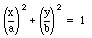
The parameter a is called the semi-major axis of the ellipse (if a > b). It corresponds to the longest distance between the center of the ellipse (x=0,y=0) and the trajectory. The parameter b is called the semi-minor axis of the ellipse (if a > b). It corresponds to the shortest distance between the center of the ellipse (x=0,y=0) and the trajectory. An ellipse has two focuses (see Figure 14.7): each focus is located on the x-axis, a distance (e a) away from the center of the ellipse. The parameter e is called the eccentricity of the ellipse and is equal to
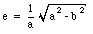
We see that for a circle the eccentricity is equal to zero, and the semi-major axis is equal to the radius of the circle. The shortest distance between the focus and the ellipse is called the perihelion distance Rp. It is easy to see that this distance is given by
Rp = a (1 - e)
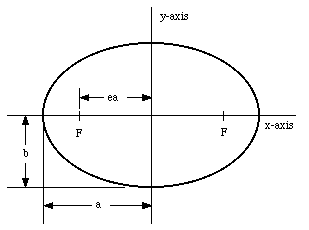
Figure 14.7. The ellipse.
The largest distance between the focus and the ellipse is called the aphelion distance Ra which is given by
Ra = a (1 + e)
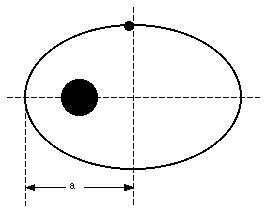
Figure 14.8. Trajectory of planet around sun.
The planets move about the sun in an elliptic path with the focus at the position of the sun (see Figure 14.8). The elliptical shape of the trajectory of the planet is a result of the 1/r2 nature of the gravitational force and the initial conditions. Under certain conditions the trajectory will be hyperbolic and the planet will approach the sun only once in its lifetime. Examples of hyperbolic trajectories are the trajectories of satellites that use the gravitational fields of the planets to change direction. The law of periods, previously derived for the special case of circular orbits, also holds for elliptical orbits, provided we replace r by a, the semi-major axis of the ellipse.
Sample Problem 14-8
Comet Halley has a period of 76 years and, in 1986, has a distance of closest approach to the sun of 8.9 x 1010 m. (a) What is the aphelion distance ? (b) What is the eccentricity of the orbit of Comet Halley ?
The semi-major axis of the orbit of Comet Halley can be found using the law of periods:
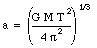
where
Rp = a (1 - e)
This equation shows that the eccentricity of the orbit can be calculated easily:
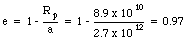
The aphelion distance can now be calculated
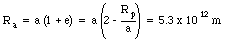
The trajectory of a planet about the sun is described by an ellipse with the sun in one of its focuses. Figure 14.9 shows the position of the planet at two instances (t and t + [Delta]t). The shaded wedge shows the area swept out in the time [Delta]t. The area, [Delta]A, is approximately one-half of its base, [Delta]w, times its height r. The width of the wedge is related to r and [Delta][theta]:
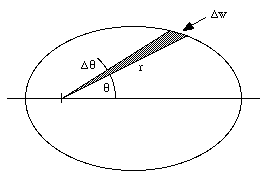
Figure 14.9. Area swept out by planet during a time [Delta]t.
[Delta]w = r [Delta][theta]
We conclude that the area [Delta]A is given by
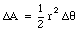
If the time interval [Delta]t approaches zero, the expression for [Delta]A becomes more exact. The instantaneous rate at which the area is being swept out is
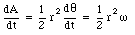
The rate at which the area is being swept out depends on the velocity of the planet and is also related to its angular momentum L. Figure 14.10 shows how to calculate the angular momentum of the planet. The angular momentum of the planet can be calculated as follows
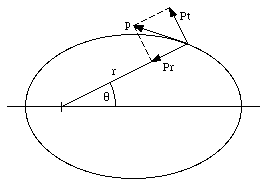
Figure 14.10. Angular momentum of planet.
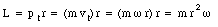
Substituting this in the expression obtained for dA/dt we conclude that
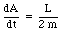
Since no external torques are acting on the sun-planet system, the angular momentum of the system is constant. This immediately indicates that dA/dt also remains constant. We conclude that
" A line joining the planet to the sun sweeps out equal areas in equal time "
This shows that the velocity of the planet will be highest when the distance between the sun and planet is smallest. The slowest velocity of the planet will occur when the distance between the sun and the planet is largest.
Suppose a satellite of mass m is in orbit around the earth (mass M). The radius of the orbit is given to be r. The kinetic and potential energy of the satellite can be easily expressed in terms of r. The potential energy of the satellite is given by
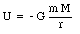
The velocity of the satellite can be found by requiring that the magnitude of the gravitational force is equal to the centripetal force:
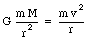
The kinetic energy can therefore given by
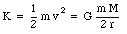
The total mechanical energy can now be calculated