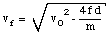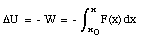
In this chapter we will discuss conservation of energy. The conservation laws in physics can be expressed in very simple form:
" Consider a system of particles, completely isolated from outside influence. As the particles move about and interact with each other, there are certain properties of the system that do not change "
In short we can express this as
X = constant
in which X is the conserved property.
A mass hanging from the ceiling will have a kinetic energy equal to zero. If the cord breaks, the mass will rapidly increase its kinetic energy. This kinetic energy was somehow stored in the mass when it was hanging from the ceiling: the energy was hidden, but has the potential to reappear as kinetic energy. The stored energy is called potential energy. Conservation of energy tells us that the total energy of the system is conserved, and in this case, the sum of kinetic and potential energy must be constant. This means that every change in the kinetic energy of a system must be accompanied by an equal but opposite change in the potential energy:
[Delta]U + [Delta]K = 0
and
E = U + K = constant
The work-energy theorem discussed in Chapter 7 relates the amount of work W to the change in the kinetic energy of the system
W = [Delta]K
The change in the potential energy of the system can now be related to the amount of work done on the system
[Delta]U = - [Delta]K = - W
which will be the definition of the potential energy. The unit of potential energy is the Joule (J).
The potential energy U can be obtained from the applied force F
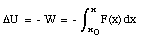
and
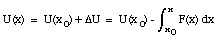
where U(x0) is the potential energy of the system at its chosen reference configuration. It turns out that only changes in the potential energy are important, and we are free to assign the arbitrary value of zero to the potential energy of the system when it is in its reference configuration.
Sometimes, the potential energy function U(x) is known. The force responsible for this potential can then be obtained
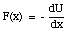
We will continue with discussing some example of conservation of energy.
The force exerted by a spring on a mass m can be calculated using Hooke's law
F(x) = - k x
where k is the spring constant, and x is the amount by which the spring is stretched (x > 0) or compressed (x < 0). When a moving object runs into a relaxed spring it will slow down, come to rest momentarily, before accelerating in a direction opposite to its original direction (see Figure 8.1). While the object is slowing down, it will compress the spring. As the spring is compressed, the kinetic energy of the block is gradually transferred to the spring where it is stored as potential energy. The potential energy of the spring in its relaxed position is defined to be zero. The potential energy of the spring in any other state can be obtained from Hooke's law
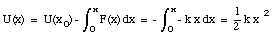
Suppose the total energy of the ball-spring system is E. Conservation of energy tells us
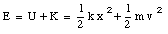
Note that the amount of work done by the spring on the block after it returns to its original position is zero.

Figure 8.1. Conversion of kinetic energy into potential energy and vice-versa.
Sample Problem 8-4
A spring of a spring gun is compressed a distance d from its relaxed state. A ball if mass m is put in the barrel. With what speed will the ball leave the barrel once the gun is fired ?
Suppose Ei is the mechanical energy of the system when the spring is compressed. Since the system is initially at rest, the total energy is just the potential energy of the compressed spring:
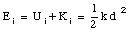
At the moment that the ball leaves the barrel, the spring is in its relaxed position, and its potential energy is zero. The total energy at that point is therefore just the kinetic energy of the moving mass:
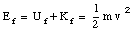
Conservation of energy requires that Ei = Ef. This means
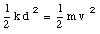
We can now calculate the velocity of the ball
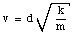
Example Problem 1
Suppose the ball in Figure 8.1 has an initial velocity v0 and a mass m. If the spring constant is k, what is the maximum compression of the spring ?
In the initial situation, the spring is in its relaxed position (U = 0). The total energy of the ball-spring system is given by
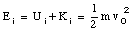
The maximum compression of the spring will occur when the ball is at rest. At this point the kinetic energy of the system is zero (K = 0) and the total energy of the system is given by
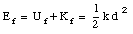
Conservation of energy tells us that Ei = Ef, and thus
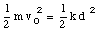
and
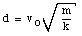
A ball moving upwards in the gravitational field of the earth will lose its kinetic energy and come momentarily to rest at its highest point. The ball than reverses its direction, steadily regaining its kinetic energy that was lost on the way up. When the ball arrives at its starting point it will have a kinetic energy equal to its initial kinetic energy. The work done by the gravitational force on the ball is negative during the upwards motion while it is positive on the way down. The work done when the ball returns to its original position is zero.
The potential energy due to the gravitational force can be calculated
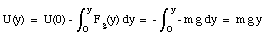
where the potential energy at y = 0 is defined to be zero. Conservation of energy for the earth-ball system now shows
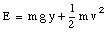
This equation holds also for a ball moving in two or three dimensions. Since Fg is perpendicular to the horizontal direction, the work done by this force on the ball is zero for a displacement in the x and/or the z-direction. In the calculation of the change in the gravitational potential energy of an object, only the displacement in the vertical direction needs to be considered.
Sample Problem 8-3
A child with mass m is released from rest at the top of a curved water slide, a height h above the level of a pool. What is the velocity of the child when she is projected into the pool ? Assume that the slide is frictionless.
The initial energy consist only out of potential energy (since child is at rest the kinetic energy is zero)
Ei = m g h
where we have taken the potential energy at pool level to be zero. At the bottom of the slide, the potential energy is zero, and the final energy consist only out of kinetic energy
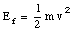
Conservation of energy requires that
Ei = Ef
Thus
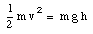
or
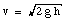
A block of mass m projected onto a rough surface will be brought to rest by the kinetic friction force. There is no way to get back the original kinetic energy of the block after the friction force has brought it to rest. The directed long-scale motion of the block has been transformed into kinetic energy of the randomly directed moving atoms that make up the block and the plane. We can not associate a potential energy with the friction force.
If a potential energy can be associated with a force, we call the force conservative. Examples of conservative forces are the spring force and the gravitational force. If a potential energy can not be associated with a force, we call that force non-conservative. An example is the friction force. Alternative tests of the conservative nature of a force are:
1. A force is conservative if the work it does on a particle that moves through a round trip is zero; otherwise, the force is non conservative. The requirement of zero work for a round trip is not met by the friction force.
2. A force is conservative if the work done by it on a particle that moves between two points is the same for all paths connecting these points; otherwise, it is non-conservative.
Test 1 and test 2 are equivalent. For example, assume that the work done for the round trip from A to B and back to A (see Figure 8.2) is zero. This means that
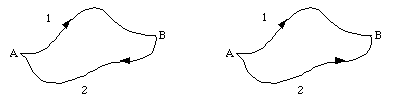
Figure 8.2. Particle on a round trip from A to B back to A, and from A to B via 2 different routes.
WAB,1 + WBA,2 = 0
or
WAB,1 = - WBA,2
The work done by the force on each segment reverses sign if we revert the direction
WAB,2 = - WBA,2
This relation than can be used to show that
WAB,1 = WAB,2
which is exactly what test 2 states (the work done by the force on the object depends only on the initial and final position of the object and not on the path taken).
Figure 8.3 shows two possible trajectories to get from A to B. What is the work done on the object by the gravitational force for trajectory 1 and for trajectory 2 ? The work done if the mass is moved along route 1 is equal to
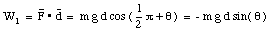
The alternate route (route 2) consist out of a motion in the horizontal direction followed by one in the vertical direction. For any motion in the horizontal plane, the gravitational force is perpendicular to the displacement. The work done by the gravitational force is therefore zero. For the motion along the vertical, the gravitational force is opposed to the motion. The work done by the gravitational force is
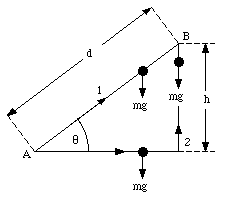
Figure 8.3. Two possible trajectories to get from A to B.
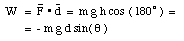
The total work done by the gravitational force on the object when it is moved from A to B via route 2 is therefore
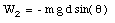
which is equal to W1.
A plot of the potential energy as function of the x-coordinate tells us a lot about the motion of the object (see for example Figure 8.12 in Halliday, Resnick and Walker). By differentiating U(x) we can obtain the force acting on the object
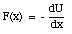
In the absence of friction the conservation of mechanical energy holds and
U(x) + K = E
Since the kinetic energy can not be negative, the particle can only be in those regions for which E - U is zero or positive. The points at which E - U = K = 0 are called the turning points. The potential energy curve (Figure 8.12 in Halliday, Resnick and Walker) shows several local maxima and minima. The force at each of these maxima and minima is zero. A point is a position of stable equilibrium if the potential energy has a minimum at that point (in this case, small displacements in either direction will result in a force that pushes the particle back towards the position of stable equilibrium). Points of unstable equilibrium appear as maxima in the potential energy curve (if the particle is displaced slightly from the position of unstable equilibrium, the forces acting on it will tend to push the particle even further away).
If we look at a block-spring system, oscillating on a rough surface, we will see that the amplitude of the motion decreases continuously. Because of the frictional force, the mechanical energy is no longer conserved. If we look at a system on which several conservative forces act, in addition to the friction force. The total work done on the system is
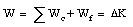
which is equal to the change in the kinetic energy of the system (work-energy theorem). Each conservative force can be identified with a potential energy and
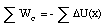
We can now rewrite the expression for the change in the kinetic energy of the system
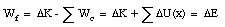
The work done by the friction force is equal to the change in the mechanical energy of the system.
In the presence of non-conservative forces, mechanical energy is converted into internal energy Uint (or thermal energy):
[Delta]Uint = - Wf
With this definition of the internal energy, the work-energy theorem can be rewritten as
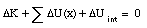
which is the law of conservation of energy. In words
" Energy may be transformed from one kind into another in an isolated system but it can not be created or destroyed; the total energy of a system always remains constant. "
Sample Problem 8-8
A ball bearing whose mass is m is fired vertically downward from a height h with an initial velocity v0 (see Figure 8.4). It buries itself in the sand at a depth d. What average upward resistive force f does the sand exert on the ball as it comes to rest ?
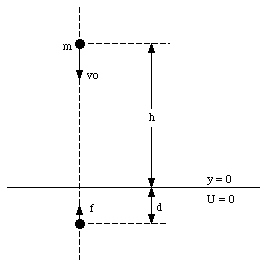
Figure 8.4. Sample Problem 5.
The work done by the friction force f is given by
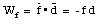
The initial mechanical energy of the system is given by
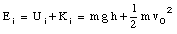
The final mechanical energy of the system consist only out of the potential energy (Kf = 0)
Ef = Uf = m g (- d) = - m g d
The change in mechanical energy is
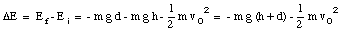
which must be equal to the work done on the bearing by the frictional force
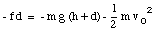
The friction force f can now be calculated
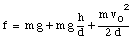
Example Problem 2
A block whose mass is m is fired up an inclined plane (see Figure 8.5) with an initial velocity v0. It travels a distance d up the plane, comes momentarily to rest, and then slides back down to the bottom of the plane. What is the magnitude of the kinetic friction force that acts on the block while it is moving ? What will the velocity be when the block returns at its original position.
The work done by the friction force is equal to the change in the mechanical energy of the system. The potential energy at the origin is taken to be zero. Therefore, the initial mechanical energy of the system is just the kinetic energy of the block
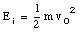
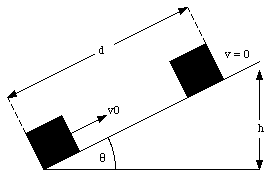
Figure 8.5. Example Problem 2.
The final mechanical energy (at maximum height) is just the potential energy of the block at height h:
Ef = m g h = m g d sin([theta])
The change in mechanical energy is
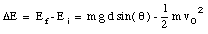
The work done on the block by the friction force is
Wf = - f d
and must be equal to [Delta]E. Thus

The friction force f can now be obtained
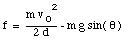
When the block returns to the origin, the friction force has again done work on the block. The total work done by the friction force on the block is now
Wf = - 2 f d
This must be equal to the change in mechanical energy of the system. When the block returns at the origin, there is no change in its potential energy. The change in the mechanical energy of the system is due to a change in the velocity of the block:
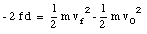
The final velocity of the block can now be calculated