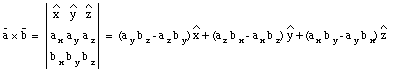and
and
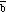 are defined. If
are defined. If
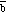 is added to
is added to
 ,
a third vector
,
a third vector
 is created (see Figure 3.1).
is created (see Figure 3.1).
The motion of a particle in one dimension is simple. Its velocity is either positive or negative: positive velocity corresponds to a motion to the right while negative velocity corresponds to a motion to the left. To describe the motion of an object in 3 dimensions, we need to specify not only the magnitude of its velocity, but also its direction: velocity is a vector. A quantity not involving a direction is a scalar. Examples of scalars are temperature, pressure and time. In this Chapter we will discuss the various vector operations that will be used in this course.
One important vector operation that we will frequently encounter is vector addition. There are two methods for vector addition: the graphical method and the analytical method. We will start discussing vector addition by using the graphical method.
Assume two vectors
 and
and
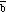 are defined. If
are defined. If
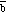 is added to
is added to
 ,
a third vector
,
a third vector
 is created (see Figure 3.1).
is created (see Figure 3.1).
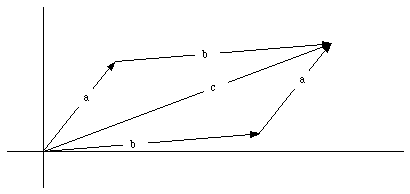
Figure 3.1. Commutative Law of Vector Addition.
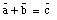
There are however two ways of combining the vectors
 and
and
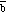 (see Figure 3.1). Inspection of the resulting vector
(see Figure 3.1). Inspection of the resulting vector
 shows that vector addition satisfies the commutative
law (order of addition does not influence the final result):
shows that vector addition satisfies the commutative
law (order of addition does not influence the final result):
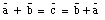
Vector addition also satisfies the associative law (the result of vector addition is independent of the order in which the vectors are added, see Figure 3.2):
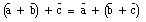
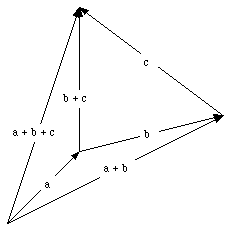
Figure 3.2. Associative Law of Vector Addition.
Figure 3.3. Vector
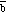 and -
and -
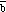
The opposite of vector
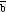 is a vector with the same magnitude as
is a vector with the same magnitude as
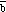 but pointing in the opposite direction (see Figure 3.3):
but pointing in the opposite direction (see Figure 3.3):
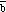 + (-
+ (-
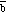 )
= 0
)
= 0
Subtracting
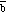 from
from
 is the same as adding the opposite of
is the same as adding the opposite of
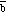 to
to
 (see Figure 3.4):
(see Figure 3.4):
 =
=
 -
-
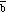 =
=
 + (-
+ (-
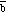 )
)
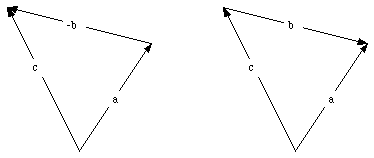
Figure 3.4. Vector Subtraction.
Figure 3.4 also shows that
 +
+
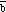 =
=
 .
.
In actual calculations the graphical method is not practical, and the vector algebra is performed on its components (this is the analytical method).
To demonstrate the use of the analytical method of vector addition, we
limit ourselves to 2 dimensions. Define a coordinate system with an x-axis and
y-axis (see Figure 3.5). We can always find 2 vectors,
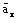 and
and
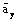 ,
whose vector sum equals
,
whose vector sum equals
 .
These two vectors,
.
These two vectors,
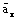 and
and
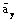 ,
are called the components of
,
are called the components of
 ,
and by definition satisfy the following relation:
,
and by definition satisfy the following relation:
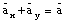
Suppose that [theta] is the angle between the vector
 and the x-axis. The 2 components of
and the x-axis. The 2 components of
 are defined such that their direction is along the x-axis and y-axis. The
length of each of the components can now be easily calculated:
are defined such that their direction is along the x-axis and y-axis. The
length of each of the components can now be easily calculated:
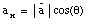
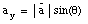
and the vector
 can be written as:
can be written as:
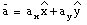
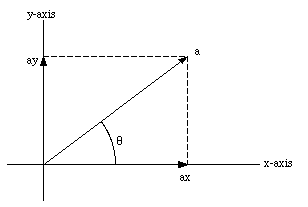
Figure 3.5. Decomposition of vector
 .
.
Note: in contrast to Halliday, Resnick, and Walker we use
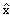 and
and
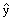 to indicate the unit vectors along the x- and y-axis, respectively (Halliday,
Resnick, and Walker use i, j, and k which is harder to
write). The decomposition of vector
to indicate the unit vectors along the x- and y-axis, respectively (Halliday,
Resnick, and Walker use i, j, and k which is harder to
write). The decomposition of vector
 into 2 components is not unambiguous. It depends on the choice of the
coordinate system (see Figure 3.6).
into 2 components is not unambiguous. It depends on the choice of the
coordinate system (see Figure 3.6).
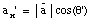
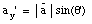
Although the decomposition of a vector depends on the coordinate system
chosen, relations between vectors are not affected by the choice of the
coordinate system (for example, if two vectors are perpendicular in one
coordinate system, they are perpendicular in every coordinate system). The
physics (and the relation between physical quantities) is also not affected by
the choice of the coordinate system, and we usually choose the coordinate
system such that our problems can be solved most easily. This was already
demonstrated in Chapter 2, where the origin of the coordinate system was
usually defined as the position of the object at time t = 0. In two or three
dimensions, we can usually choose the coordinate system such that one of the
vectors coincides with one of the coordinate axes. For example, if the
coordinate system is defined such that the direction of
 is along the x-axis, the components of
is along the x-axis, the components of
 are:
are:
ax = a
ay = 0
az = 0
Figure 3.6. Decomposition of vector
 in different coordinate systems.
in different coordinate systems.
Vector algebra using the analytical method is based on the following rule:
"Two vectors are equal to each other if their corresponding components are equal"
Applying this rule to vector addition:
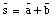
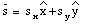
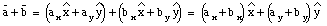
Comparing the equations for
 and
and
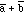 ,
we can conclude that since
,
we can conclude that since
 is equal to
is equal to
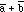 ,
their components are related as follows:
,
their components are related as follows:
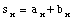
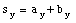
These relations describe vector addition using the analytical technique (and similar relations hold for vector addition in three dimensions).
We have just described how to find the components of a vector if its
magnitude and direction are provided. If the components of a vector are
provided, we can also calculate its direction and magnitude. Suppose the
components of vector
 along the x-axis and y-axis are ax and ay, respectively.
The length of the vector
along the x-axis and y-axis are ax and ay, respectively.
The length of the vector
 can be easily calculated:
can be easily calculated:
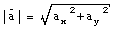
The angle [theta] between the vector
 and the positive x-axis can be obtained from the following relation (see also
Figure 3.5):
and the positive x-axis can be obtained from the following relation (see also
Figure 3.5):
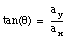
Note: one should exercise great care in using the previous relation for [theta]. Atan(ay/ax) has 2 solutions; any calculator will return the solution between - [pi]/2 and [pi]/2. The correct solution will depend on the sign of ax:
if ax > 0: - [pi]/2 < [theta] < [pi]/2
if ax < 0: [pi]/2 < [theta] < 3[pi]/2
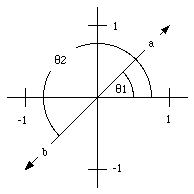
Figure 3.7. Example of angle ambiguity.
Example: The two vectors shown in Figure 3.7 can be written as:
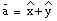
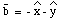
It is clear that for both vectors: atan([theta]) = 1. For vector
 ,
the solution is [theta] = 45deg., while for vector
,
the solution is [theta] = 45deg., while for vector
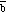 ,
the solution is [theta] = 135deg.. Note that ax = 1 > 0, and
bx = -1 < 0.
,
the solution is [theta] = 135deg.. Note that ax = 1 > 0, and
bx = -1 < 0.
The product of a vector
 and a scalar s is a new vector, whose direction is the same as that of
and a scalar s is a new vector, whose direction is the same as that of
 if s is positive or opposite to that direction if s is negative (see Figure
3.8). The magnitude of the new vector is the magnitude of
if s is positive or opposite to that direction if s is negative (see Figure
3.8). The magnitude of the new vector is the magnitude of
 multiplied by the absolute value of s. This procedure can be summarized as
follows:
multiplied by the absolute value of s. This procedure can be summarized as
follows:
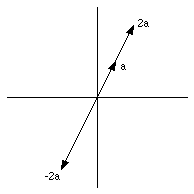
Figure 3.8. Multiplying a vector by a scalar.
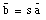
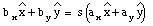
Since two vectors are only equal only if their corresponding components
are equal, we obtain the following relation between the components of
 and the components of
and the components of
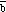 :
:
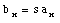
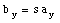
The following relations are summarizing the relations between the
magnitude and direction of the vectors
 and
and
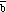 :
:
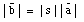
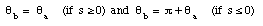
Two vectors
 and
and
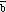 are shown in Figure 3.9. The angle between these two vectors is [phi]. The
scalar product of
are shown in Figure 3.9. The angle between these two vectors is [phi]. The
scalar product of
 and
and
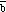 (represented by
(represented by
 .
.
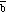 )
is defined as:
)
is defined as:
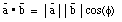
In a coordinate system in which the x, y and z-axes are mutual perpendicular, the following relations hold for the scalar product between the various unit vectors:
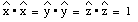
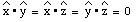
Suppose that the vectors
 and
and
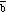 are defined as follows:
are defined as follows:
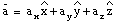
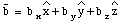
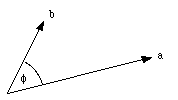
Figure 3.9. Scalar Product of vectors
 and
and
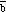 .
.
The scalar product of
 and
and
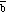 can now be rewritten in terms of the scalar product between the unit vectors
along the x, y and z-axes:
can now be rewritten in terms of the scalar product between the unit vectors
along the x, y and z-axes:
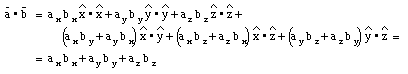
Note that in deriving this equation, we have applied the following rule:
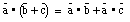
An alternative derivation of the expression of the scalar product in
terms of the components of the two vectors can be easily derived as follows
(see Figure 3.10). The components of
 and
and
 are given by:
are given by:
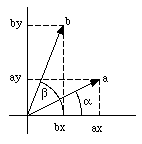
Figure 3.10. Alternative Derivation of Scalar Product.
ax = a cos(a)
ay = a sin(a)
bx = b cos([beta])
by = b sin([beta])
The scalar product can now be obtained as follows:
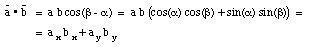
What is so useful about the scalar product ? If two vectors are
perpendicular, their relative angle equals 90deg., and
 .
.
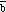 = 0. The scalar product therefore provides an easy test to determine whether
two vectors are perpendicular. Suppose
= 0. The scalar product therefore provides an easy test to determine whether
two vectors are perpendicular. Suppose
 and
and
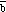 are defined as follows:
are defined as follows:
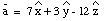
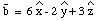
These two vectors are perpendicular since:
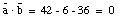
In a similar manner we can easily determine whether the angle between
the two vector is less than 90deg. (in which case
 .
.
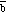 > 0) or more than 90deg. (in which case
> 0) or more than 90deg. (in which case
 .
.
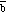 < 0)
< 0)
The vector product of two vectors
 and
and
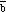 ,
written as
,
written as
 x
x
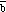 ,
is a third vector
,
is a third vector
 with the following properties:
with the following properties:
 is given by:
is given by:
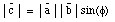
where [phi] is the smallest angle between
 and
and
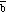 .
Note: the angle between
.
Note: the angle between
 and
and
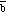 is [phi] or 360deg. - [phi]. However, since sin([phi]) = - sin(2[pi] - [phi]),
the vector product is different for these two angles.
is [phi] or 360deg. - [phi]. However, since sin([phi]) = - sin(2[pi] - [phi]),
the vector product is different for these two angles.
 is perpendicular to the plane defined by
is perpendicular to the plane defined by
 and
and
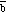 ,
and the direction (up or down) is determined using the right-hand rule.
,
and the direction (up or down) is determined using the right-hand rule.It is clear from the definition of the vector product that the order of the components is important. It can be shown, by applying the right hand rule, that the following relation holds:
 x
x
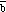 = -
= -
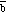 x
x

The following expression can be used to calculate
 x
x
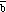 if the components of
if the components of
 and
and
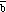 are provided:
are provided: