1. Review the results of Exam # 2. Focus on the multiple-choice questions and on Problem 11.

2. The Egyptian pyramids, made of a total of about 25 million tons of limestone, were built entirely with human labor. To get some insight into how this might have been accomplished, consider lifting a "small" pyramid stone with a weight of 20,000 N, which is about 2 tons (some of the larger stones actually weigh up to 70 tons).

a) Estimate the number of able-bodied people it would take to lift such a stone off the ground. Begin by deciding how much a typical person (such as you) can lift.

Now consider lifting the stone with the following arrangement, consisting of two long levers resting on sturdy pivot points (sometimes called fulcrums). The downward arrows represent the forces applied by the workers.

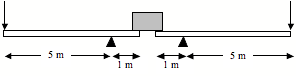
b) Make a free body diagram of one of the levers as it is lifting the stone. You can neglect the weight of the lever itself.

c) Write out the torque equation for the lever, choosing the fulcrum as the axis of rotation.

d) How much force must be applied to the end of each lever in order to lift the stone at a steady rate?

Other things to consider:

Look carefully at the sketch of the levers and the block. You’ll see that the distance between each fulcrum and the end of each lever is not exactly the same as the distance between the fulcrum and the edge of the block. Which distance should be used as the lever arm of the force exerted by the block on the lever, and why?

What might the limitations of a simple lever system be?

Can you determine the force exerted on the lever by the fulcrum?

3. Consider a ladder of mass M and length L leaning against a wall at some angle q, as shown in the sketch to the right. The bottom of the ladder is rubberized (so there's a lot of friction), but the top is bare aluminum and can be considered frictionless.

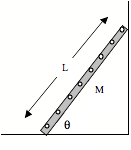
a) Make a free-body diagram for this ladder, including a coordinate system.

b) Write out the equations for static equilibrium of the ladder. (Indicate with a “P” on your FBD the point you are choosing to sum torques around, and show with an arrow your choice for the direction of a positive torque.)

c) In terms of the known quantities (M, L and q), determine all of the forces exerted on the ladder by the wall and by the floor.

Other things to consider:

Suppose someone is standing on the ladder. Which forces on the ladder do you expect to be different, and will they be bigger or smaller? Show explicitly how your equations will be modified.

4. For the same ladder above suppose that the coefficient of static friction between the floor and the ladder is known to be m = 1/2.

a) What is the maximum amount of friction that the floor can exert on the ladder? Express your result as a multiple of the weight of the ladder (examples: f = 2mg or f = 0.25mg).

b) At what angle q is the frictional force at its maximum?

c) What would happen to the ladder if q were made smaller?

Other things to consider:

The coefficient of friction between the ladder and the floor is a constant number. How then do you explain (in words) the fact that the ladder becomes unstable as the angle q is decreased?

Which is more likely to slip when leaned against the wall as in this problem, a tall ladder or a short ladder? Assume that the ladders have the same rubber on the bottom.