1. The Sun’s gravitational pull on the Earth is much larger than the Moon’s. Yet, the Moon’s gravitational pull is mainly responsible for the tides. Can you explain this?

2. The Sun is directly below us at midnight, in line with the Earth’s center. Are we then heavier at midnight, due to the Sun’s gravitational force on us, than we are at noon? Make an estimate of the difference in weight (if any).

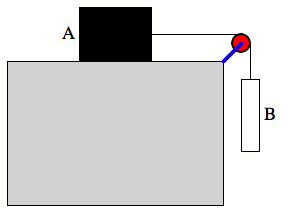
3. Consider the system shown below. The coefficient of kinetic friction between block A (with weight W_a) and the table top is m_k. (a) Calculate the weight W_b of the hanging block required if this block is to descend at constant speed once it has been set into motion. (b) Suppose the coefficient of static friction is m_s = 0.4 and the mass of A is 30 kg and the mass of B is 2 kg. What is the force of friction on mass A now (assuming an initial condition of no motion)? How will the system move as time increases?

4. The density of a certain planet varies with radial distance as r(r) = r₀(1-ar/R₀) where R₀ is the radius of the planet, r₀ is its central density, and a is a dimensionless constant. (a) What is the total mass of the planet? (b) Calculate the weight of a one-kilogram mass located on the surface of the planet.

5. The Earth moves faster in its orbit around the sun in December than in June. Is it closer to the Sun in June or in December? Does this effect the seasons? Explain.

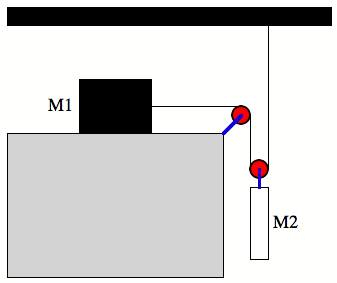
6. Consider the drawing below. In terms of M₁, M₂ and g, find the acceleration of each block in the system. Assume there is no friction anywhere in the system. Check your solution with limiting cases.