Problem 1 (1.25 points)

A rocket is fired vertically upward with a constant acceleration greater than g. The rocket engine runs for several seconds and then stops. Which of the following statements is true if we plot the velocity of the rocket as a function of time?

c The velocity versus time graph will be parabolic.

c The velocity versus time graph will be a straight line.

c The velocity versus time graph will consist of two straight-line segments, both with a positive (but different) slope.

g The velocity versus time graph will consist of two straight-line segments with slopes of opposite sign.

Problem 2 (1.25 points)

Which of the following units may be used to describe linear momentum?

g Ns

c N/s

c Nm

c N/m

Problem 3 (1.25 points)

Suppose Newton’s Law of Universal Gravitation were modified to read: F = GmM/r3, rather than the observed inverse-square law force. Kepler’s third law would then read

c (T₁/T₂)² = (r₁/r₂)

c (T₁/T₂)² = (r₁/r₂)³

g (T₁/T₂)² = (r₁/r₂)⁴

c (T₁/T₂)² = (r₁/r₂)²

Problem 4 (1.25 points)

Two masses m₁ and m₂ sit on a table connected by a rope. A second rope is attached to the opposite side of m₂. Both masses are pulled along the table with the tension in the second rope equal to T₂. Let T₁ denote the tension in the first rope connecting the two masses. Which of the following statements is true?

c T₁ = T₂

c T₁ > T₂

g T₁ < T₂

c We need to know the relative values of m₁ and m₂ to answer this question.

Problem 5 (1.25 points)

The linear density of a long thin rod, of length L, decreases from a value of d at the left end to zero at the right end. How far from the left end is the rod’s center-of-mass located?

c L/5

g L/3

c (2/3) L

c (4/5) L

Problem 6 (1.25 points)

A sphere rolling on a horizontal flat surface slows down because of

c the friction force.

g the deformation of the surface.

c the ball and the surface are essentially rigid.

c the gravitational force.

Problem 7 (1.25 points)

Three balls start at the same vertical position but follow different frictionless paths as they descent from a height h. Which of the following statements is true?

c The balls all reach the lower level at the same time.

g The balls all reach the lower level with the same speed but at possibly different times.

c The ball that takes the longer path reaches the bottom with the lowest velocity.

c The balls all reach the lower level with the same speed and at the same time.

Problem 8 (1.25 points)

Suppose you are holding a bicycle wheel by a handle connected to the axle in front of you. The axle points horizontally away from you and the wheel is spinning clockwise from your perspective. Now try to tilt the axle to your left (center of mass moves leftward). The wheel will swerve

g upward

c downward

c to your left

c to your right

Problem 9 (1.25 points)

An ideal gas undergoing a “free expansion”

c does positive work.

c increases its internal energy.

c decreases its internal energy.

g does not change its internal energy.

Problem 10 (1.25 points)

The coefficient of performance of a Carnot engine operated as a heat pump is

c 1 – T_L/T_H

g (1 - T_L/T_H)^-1

c (T_H/T_L - 1)^-1

c T_H/T_L – 1

Problem 11

a. The heat exchange takes place at constant volume, and we thus must use the molar specific heat for constant volume C_V. For an ideal monatomic gas, C_V = (3/2)R. The heat added or removed is proportional to the temperature difference. For the Otto engine, the find the following values:

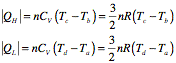
b. The efficiency of the heat engine is defined as

Using the results of part (a) we can rewrite this in terms of the temperature:

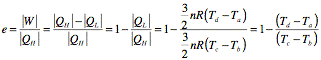
c. During the adiabatic compression and expansion, the pressures and volumes are related in the following manner:

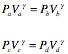
Using the idea gas law we can replace the pressure by the temperature (P = nRT/V) and rewrite these relations as

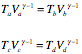
The efficiency can now be rewritten as

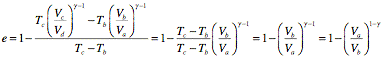
In this step we have used the fact that V_c = V_b and V_d = V_a.

d. The constant g is related to the molar specific heats:

We see that when C_V increases, g decreases. The molar specific heat at constant volume for a monatomic gas is smaller than the molar specific heat at constant volume for a diatomic gas since the diatomic gas has more degrees of freedom. As a result, g decreases when we replace the monatomic gas with a diatomic gas. Since the compression factor is larger than 1, a decrease in g will result in an increase in (V_a/V_b)^1-g and a decrease in the efficiency e.

Problem 12

a. Due to the symmetry of the system, the net force acting on each mass will be pointing towards the center of the triangle:

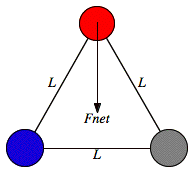
b. In order to determine the magnitude of the net force acting on one of the masses, we need to determine the proper component of each of the two gravitational forces acting on each mass (see Figure).

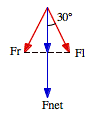
The magnitude of the force exerted on one mass by the one of the other masses is

The component of this force directed towards the center of the triangle is

The magnitude of the net force acting on each mass is the sum of the gravitational forces due to both other masses, and is thus equal to

c. Since the masses carry out circular motion around the center of the triangle, the net force on each mass must be equal to

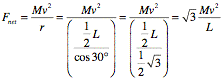
Comparing this result with the result obtained in part b we conclude that

or

Problem 13

a. There are four forces acting on the ladder: the gravitational force mg, the normal force N exerted by the floor on the ladder, the static friction force f_s, and the normal force N_W exerted by the wall on the ladder. There fours forces are shown in the free-body diagram shown below.

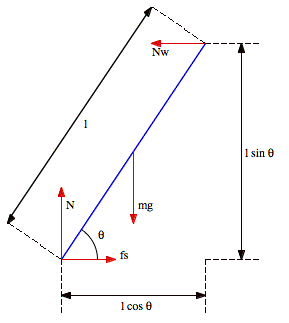
b. Since the system is in equilibrium, the torque of all forces with respect to the contact point with the ground must be zero. This requires that

The force exerted by the wall is thus equal to

c. Since the net forces in the horizontal and in the vertical direction must be 0 N we can immediately determine the magnitudes of the forces that acts on the contact point with the ground:

and

The maximum static friction force is m_sN = m_smg. The ladder is stable if

This requires that

The minimum angle at which the system is stable is thus equal to

Problem 14

a. The total angular momentum is the vector sum of the angular momentum associated with the blocks and the angular momentum associated with the pulley. The direction of the angular momentum associated with each of these components will be directed out of the paper.

The angular momentum associated with block 1 is equal to

The angular momentum associated with block 2 is equal to

Since the cord is not slipping, the pulley must be rotating with an angular velocity w = v/R₀. The angular momentum associated with the rotation of the pulley is equal to

The total angular momentum is thus equal to the vector sum of all of these components:

b. The change in the angular momentum of the system per unit time is equal to

The change in the angular momentum per unit time is also equal to the total external torque acting on the system. In the current system, the total external torque is just equal to the torque associated with the weight of mass M₂, which is equal to

Combining the last two expressions we find

and this equation can be used to determine the linear acceleration a:

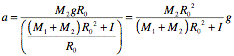
Problem 15

a. In this problem we will take the height of the ball when it is at it lowest point as our reference height, and set the potential energy at this height equal to 0 J. When the ball is released from rest, its total mechanical energy will be equal to just its potential energy: E_i = MgL. At its lowest point, the potential energy will be equal to 0 J, and the total mechanical energy will be equal to the kinetic energy of the ball:

Since energy is conserved, the kinetic energy at the lowest point must be equal to the initial potential energy:

The velocity at the lowest point is thus equal to

b. Since the ball carries out circular motion, the net force acting on it must be directed towards the end of the cord and has a magnitude equal to

This net force on mass M must be provide by the gravitational force and the tension in the cord:

The tension in the cord can now be determined:

c. When the ball reaches the top of the circular path about the peg, it will have both kinetic and potential energy:

Since energy is conserved we must require that

The velocity at the top of the loop is thus equal to

d. When the ball reaches the top of its circular path about the peg it is carrying out circular motion, and there must be a net force acting on it, directed towards the peg, with a magnitude equal to

The net force is provide by the tension in the cord and the gravitational force:

The tension in the cord is thus equal to

Problem 16

a. We can apply conservation of energy to determine the velocity of the small cube just before it collides with the smaller cube:

The velocity of the small cube just before the collision is thus equal to

Applying the equations for elastic collisions in one dimension, we can determine the velocity of the larger cube right after the collision:

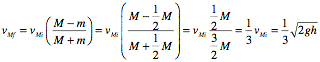
b. Applying the equations for elastic collisions in one dimension, we can determine the velocity of the larger cube right after the collision:

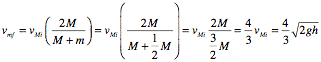
c. Both blocks carry out projectile motion, and the velocities calculated in parts a and b are the initial horizontal components of the projectile motion (the vertical component is equal to 0 m/s). The time required for the blocks to fall to the ground can be easily calculated by requiring that y(t) = -H:

The time t is thus equal to

The horizontal displacement of the larger cube during this period is equal to

The horizontal displacement of the smaller cube during this period is equal to

The distance between the positions where the two cubes hits the ground is thus equal to

Problem 17

a. The first thing to do in this problem is to draw a force diagram and choose the direction of positive acceleration. We will use the convention that a positive acceleration is a downwards directed acceleration.

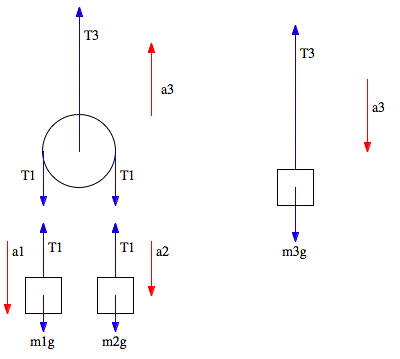
Let’s consider first the motion of the two masses m₁ and m₂ with respect to the moveable pulley. If the acceleration of mass m₁ with respect to the moveable pulley is a_r, then mass m₂ will have an acceleration -a_r with respect to the moveable pulley. Since the moveable pulley is accelerating up with an acceleration a₃, the net accelerations of masses m₁ and m₂ will be equal to

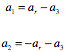
Since the pulleys are massless, the net force acting on them must be 0 N. Thus, looking at the moveable pulley we conclude that 2T₁ = T₃. The net force on each mass must be equal to the ma, and for each block we get the following force requirement:

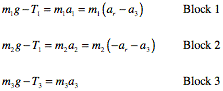
Adding the equations for blocks 1 and 2 and subtracting the equation for block 3, we can express the acceleration a_r in terms of a₃:

This tells us that

If we subtract the equation for block 1 from the equation for block 2 we can find another expression for the acceleration a_r in terms of a₃:

This tells us that

From the two expressions for a_r we can determine the acceleration of block 3:

b. The acceleration of block 2 can now be found easily:

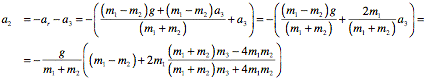
c. The acceleration for block 1 can also be found easily:

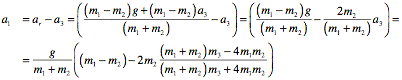
d. The tension T₃ is equal to

e. The tension T₁ is equal to