Physics 121, Final Exam
Do not turn the pages of the exam until
you are instructed to do so.
You are responsible for reading the following rules
carefully before beginning.
Exam rules: You may
use only a writing instrument while
taking this test.
You may not
consult any calculators, computers, books, notes, or each other.
Procedure:
1. Answer the multiple-choice questions (problems 1 – 10) by marking your answer on the scantron form. For each multiple-choice question (problems 1 – 10), select only one answer. Questions with more than one answer selected will be considered incorrect.
2. The analytical problems (11 – 17) must be answered in the blue exam booklets. You must answer problems 11, 12, 13, and 14 in one of the blue booklets, and problems 15, 16, and 17 in the other blue booklet. If you do not follow this convention there is no guarantee that the problems that appear in the wrong booklet will be graded.
3. The answer to each analytical problem must be well motivated and expressed in terms of the variables used in the problem. You will receive partial credit where appropriate, but only when we can read your solution. Answers that are not motivated will not receive any credit, even if correct.
4. At the end of the exam, you must hand in the blue exam
booklets, the scantron form, the exam, and the formula sheets. All items must be clearly labeled with
your name and student ID number. If
any of these items is missing, we will not grade your exam, and you will
receive a score of 0 points.
Note: You are not
allowed to use a cheat sheet on this exam. Please refer to the formula sheet at the end of this package
for important equations.
Note: If you do not
answer a question in terms of the variables provided, you will not receive
credit for that question.
Note: You will get 2.5 extra
points if you put your student ID correctly on your scantron form and answer
the analytical questions in the correct exam booklet.
Problem 1 (1.25 points)
A rocket is fired vertically upward with a constant acceleration greater than g. The rocket engine runs for several seconds and then stops. Which of the following statements is true if we plot the velocity of the rocket as a function of time?
c The velocity versus time graph will be parabolic.
c The velocity versus time graph will be a straight line.
c The velocity versus time graph will consist of two straight-line segments, both with a positive (but different) slope.
c The velocity versus time graph will consist of two straight-line segments with slopes of opposite sign.
c Ns
c N/s
c Nm
c N/m
Problem 3 (1.25 points)
Suppose Newton’s Law of Universal Gravitation were modified to read: F = GmM/r3, rather than the observed inverse-square law force. Kepler’s third law would then read
c (T1/T2)2 = (r1/r2)
c (T1/T2)2 = (r1/r2)3
c (T1/T2)2 = (r1/r2)4
c (T1/T2)2 = (r1/r2)2
Problem 4 (1.25 points)
Two masses m1 and m2 sit on a table connected by a rope. A second rope is attached to the opposite side of m2. Both masses are pulled along the table with the tension in the second rope equal to T2. Let T1 denote the tension in the first rope connecting the two masses. Which of the following statements is true?
c T1 = T2
c T1 > T2
c T1 < T2
c We need to know the relative values of m1 and m2 to answer this question.
Problem 5 (1.25 points)
The linear density of a long thin rod, of length L, decreases from a value of d at the left end to zero at the right end. How far from the left end is the rod’s center-of-mass located?
c L/5
c L/3
c (2/3) L
c (4/5) L
Problem 6 (1.25 points)
A sphere rolling on a horizontal flat surface slows down because of
c the friction force.
c the deformation of the surface.
c the ball and the surface are essentially rigid.
c the gravitational force.
Problem 7 (1.25 points)
Three balls start at the same vertical position but follow different frictionless paths as they descent from a height h. Which of the following statements is true?
c The balls all reach the lower level at the same time.
c The balls all reach the lower level with the same speed but at possibly different times.
c The ball that takes the longer path reaches the bottom with the lowest velocity.
c The balls all reach the lower level with the same speed and at the same time.
Problem 8 (1.25 points)
Suppose you are holding a bicycle wheel by a handle connected to the axle in front of you. The axle points horizontally away from you and the wheel is spinning clockwise from your perspective. Now try to tilt the axle to your left (center of mass moves leftward). The wheel will swerve
c upward.
c downward.
c to your left.
c to your right.
Problem 9 (1.25 points)
An ideal gas undergoing a “free expansion”
c does positive work.
c increases its internal energy.
c decreases its internal energy.
c does not change its internal energy.
Problem 10 (1.25 points)
The coefficient of performance of a Carnot engine operated as a heat pump is
c 1 – TL/TH
c (1 - TL/TH)-1
c (TH/TL - 1)-1
c TH/TL – 1
Problem 11 (12.5 points)
The operation of an automobile internal combustion engine can be approximated by a reversible cycle known as the Otto cycle, whose PV diagram is shown in the Figure below. The gas in cylinder at point a is compressed adiabatically to point b. Between point b and point c, heat is added to the gas, and the pressure increases at constant volume. During the power stroke, between point c and point d, the gas expands adiabatically. Between point d and point a, heat is removed from the system, and the pressure decreases at constant volume. Assume the gas is an ideal monatomic gas.
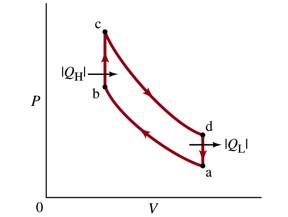
(a) Assuming there are n moles of gas in system, what are the heats |QH| and |QL|? Express your answer in terms of n, R, Ta, Tb, Tc, and Td.
(b) What is the efficiency of the Otto cycle? Express your answer in terms of Ta, Tb, Tc, and Td.
(c) Express the efficiency of the Otto cycle in terms of just the compression ratio Va/Vb and g. Hint: use the fact that during an adiabatic process PVg = constant.
(d) How does the efficiency change when we replace the monatomic gas with a diatomic gas?
Problem 12 (12.5 points)