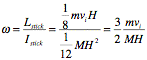Problem 1 (2.5 points)

Which of the following is not a vector?

c Angular velocity.

c Angular acceleration.

g Angle.

c Torque.

Problem 2 (2.5 points)

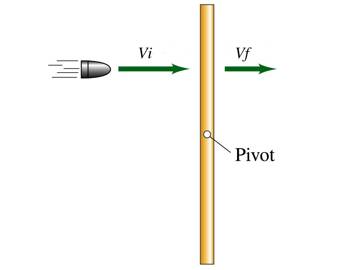
As you hold the string, a yoyo is released from rest so that gravity pulls it down, unwinding the string. What is the angular acceleration of the yoyo, in terms of the string radius R, the moment of inertia I, and the mass M?

c g/(R + 2I/(MR))

c gMR/I

g gMR/(I + MR²)

c g/R

Problem 3 (2.5 points)

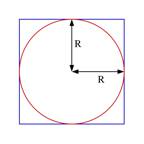
The moment of inertia of a square plate of area 4R² and mass M, with respect to an axis through its center and perpendicular to the plate, is equal to (2/3)MR². A disk of radius R is removed from the center of the plate (see Figure). What is the moment of inertia of the remaining material with respect to the same axis?

c (p/8)MR²

c (1/3 - p/12)MR²

c (1/6)MR²

g (2/3 - p/8)MR²

Problem 4 (2.5 points)

St_cm = dL_cm/dt

c only if the center of mass is at rest

c only if the center of mass is not accelerating

g even if the center of mass is accelerating

c even if the center of mass is accelerating, provided the torque is constant

Problem 5 (2.5 points)

The precession rate of the a spinning top

c is proportional to its angular momentum

c does not depend upon its angular momentum

g is inversely proportional to its angular momentum

c is inversely proportional to its kinetic energy

Problem 6 (2.5 points)

Which of the following is the greatest for concrete?

c tensile strength

g compressive strength

c shear strength

Problem 7 (2.5 points)

An object will return to its original length if the applied force is removed, provided it has not exceeded its

c proportionality limit

c breaking point

c elastic modulus

g elastic limit

Problem 8 (2.5 points)

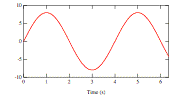
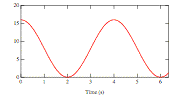
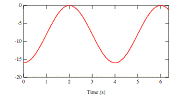
Consider the following graph, showing position versus time for simple harmonic motion.

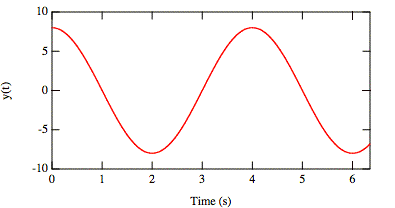
What is the frequency of this motion?

g 0.25 Hz

c 0.50 Hz

c 1.0 Hz

c 4.0 Hz

Problem 9 (2.5 points)

Consider simple harmonic motion with amplitude A. At what displacement in x is the energy shared equally between kinetic energy and potential energy?

c A

c A/2

c √2 A

g A/√2

Problem 10 (2.5 points)

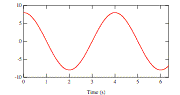
Which of the following graphs could represent the kinetic energy of simple harmonic motion as function of time?

A	B
C	D

c A

c B

g C

c D

Problem 11 (25 points)

a. When we move the block to the right, the left spring will be stretched by a distance x and the right spring will be compressed by a distance x. Both springs will exert a force to the left, and the total force is equal to

b. The equation of motion for simple-harmonic motion can be written as

The equation of motion for mass m is given by

Comparing these two equations we can immediately determine the angular frequency w:

The period of the motion is thus equal to

c. When we move the block to the right, both springs will be stretched. Suppose spring 1 is stretched by a distance x₁ and spring 2 is stretched by a distance x₂. Since the block is moved by a distance x, we must require that x = x₁ + x₂. Since the block is held at this position, the system is at rest, and the net force acting on the point where the two springs are joined must be equal to 0. This requires that

We thus have two equations with two unknown, x₁ and x₂, which we solve:

The distances x₁ and x₂ are thus equal to

and

The force on mass m is equal to the force exerted by spring 2. This force is directed towards the left:

d. The equation of motion of the block is equal to

Comparing this with the equation of motion for simple-harmonic motion we can immediately determine the angular frequency:

The period of the motion is thus equal to

Problem 12 (25 points)

a. There are three forces acting on the trailer: the gravitational force, the normal force exerted by the ground on the wheels at A, and the normal force exerted by the pin at B. These three forces are shown in the following free-body diagram.

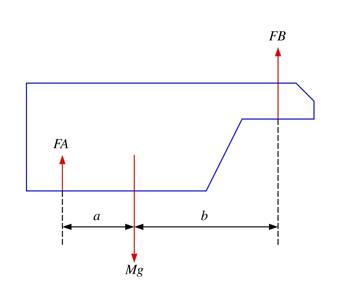
b. Since the trailer is in equilibrium, the net force in all directions and the net torque in all directions must be zero. Consider the net torque with respect to point B:

We immediately can use this equation to determine the force exerted by the road on the tires:

c. The force exerted in the trailer by the pin support at B can be found most easily by using the requirement that the net force in the vertical direction must be zero. This requires that

The force at B is thus equal to

Problem 13 (25 points)

a. The arm of the initial linear momentum is H/4. The magnitude of the initial angular momentum is equal to

Using the right-hand rule we can determine that the angular momentum is directed into the paper.

b. The arm of the final linear momentum is H/4. The magnitude of the initial angular momentum is equal to

Using the right-hand rule we can determine that the angular momentum is directed into the paper.

c. If we consider the bullet and the stick together, the collision force is an internal force and there are no external forces acting on the system. The external torque is thus equal to zero, and angular momentum will be conserved. Since the stick is initially at rest, its initial angular momentum will be equal to 0 kg m²/s. Using conservation of angular momentum we can determine the angular momentum of the stick after the collision:

The moment of inertia of the stick is equal to (1/12)MH². The angular speed of the stick after the collision is thus equal to

d. The initial kinetic energy of the system is just the kinetic energy of the bullet. It is equal to

The final kinetic energy is the sum of the kinetic energy of the bullet and the kinetic energy of the rotating rod. The former is equal to

The final kinetic energy of the stick is equal to

The final kinetic energy is thus equal to

We immediately see that the final kinetic energy is less than the initial kinetic energy as long as (3/4)(m/M) < 3 or m < 4 M. The energy that is lost in the interaction is equal to