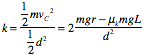Problem 1 (2.5 points)

Suppose the radius of the Earth was doubled while its density was kept fixed.  The value of the gravitational acceleration at the surface would

g   increase by a factor of 2.

c   decrease by a factor of 2.

c   remain the same.

 

Problem 2 (2.5 points)

The weight of an object in a cavern below the EarthÕs surface is

c   greater than its weight at the surface.

g   less than its weight at the surface.

c   equal to its weight at the surface.

 

Problem 3 (2.5 points)

Two objects, each of mass m, are placed on the x axis, one at x = d and the other at x = -d.  The gravitational force due to these two objects on an object located on the y axis takes on its maximum magnitude at

c   y = 0

c   y = ´

c   y = ±d

g   y = ±d/Ã2

 

Problem 4 (2.5 points)

A box (mass 5 kg) is accelerated by a force F across the floor with an acceleration of 2 m/s2 for 10 s.  The work done by the force is

c   50 J

c   100 J

g   1000 J

c   1500 J

 

Problem 5 (2.5 points)

The work done by a force F = k |x| on an object moving along the x axis directly from x = -2 m to x = +2 m is

c   0 J

c   2k

g   4k

c   8k

 

Problem 6 (2.5 points)

What is the force that corresponds to the potential energy function U(x, y) = 3xy + 5x2 + 6y3?

c   F = 5x2i + 6y3j

c   F = 3xyi + 3xyj

g   F = (-3y – 10x)i + (-3x – 18y2)j

c   F = (3y + 10x)i + (-3x – 18y2)j

 

Problem 7 (2.5 points)

A ball is dropped from a height h and hits the ground with speed v.  To have the ball hit the ground with a speed 2v it should be dropped from a height

c   h

c   2h

c   3h

g   4h

 

Problem 8 (2.5 points)

Three uniform spheres of radii 2R, R, and 3R are placed in contact next to each other on the x axis in this order (the smallest sphere is in the center, the 2R sphere is located to the left, and the 3R sphere is located to the right).  The centers of the spheres are located on the x axis.  What is the distance from the center of mass of this system from the center of the smallest sphere, assuming that each sphere has the same density?

g   (7/3)R

c   (1/3)R

c   (3/7)R

c   (65/36)R

 

Problem 9 (2.5 points)

If the kinetic energy of an auto triples because of a speed change, its linear momentum

c   increases by a factor of 3.

c   remains the same.

c   increases by a factor 9.

g   increases by a factor of Ã3.

 

Problem 10 (2.5 points)

A tennis ball moving with a speed of 10 m/s collides elastically in a head-on collision with a massive locomotive engine moving with a speed of 10 m/s towards the ball.  After bouncing directly back, the ball has a speed of

c   10 m/s.

c   20 m/s.

g   30 m/s.

c   40 m/s.

 

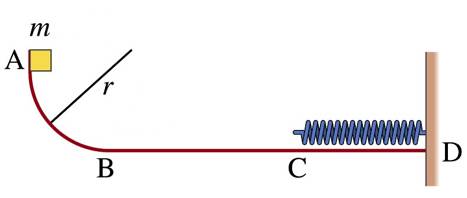
Problem 11 (25 points)

a.     Since the mass m is located on the axis of the ring, the net force due to the ring will be directed along the axis of the ring towards its center (the components perpendicular to axis will cancel).

 

b.     The distance of mass m to a small section of the ring is equal to Ã(x2 + R2).  Assuming the small section of the ring has a mass dM, we can easily calculate the magnitude of the gravitational force it exerts on m:

 

 

      The component of this force that is directed along the axis of the ring is equal to

 

 

      The total force directed along the axis of the ring is thus equal to

 

 

c.     The potential energy due to a small segment of the ring with mass dM is equal to

 

 

The potential energy due to the entire ring can now be obtained by integrating over the entire ring.  Since each point on the ring is the same distance from mass m the integral can be easily evaluated:

 

 

d.     Since the particle is initially at rest, its initial kinetic energy is equal to 0 J.  The initial mechanical energy of the system is equal to the potential energy and it thus equal to

 

 

The potential energy at the center of the ring can be obtained from the result of part (c):

 

 

The total mechanical energy at the cent of the ring must be the same as the initial mechanical energy:

 

 

This equation can be used to determine the velocity v of the particle:

 

 

 

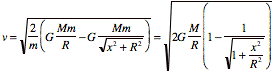
Problem 12 (25 points)

a.     The collision between the bullet and the second block is a completely inelastic collision.  After the collision, the bullet and block are moving with a velocity v2.  The linear momentum of the system at this time is thus equal to

 

 

Before the bullet hits the second block, it has a velocity vbullet,12.  At this time, the second block is at rest, and the linear momentum of the bullet and the second block is thus equal to

 

 

Conservation of linear momentum requires that

 

 

The velocity of the bullet is thus equal to

 

 

b.     The initial speed of the bullet can be found in two different ways.  We can either use the result of part (a) and use conservation of linear momentum for a system consisting out of the bullet and block 1, or we can apply conservation of linear momentum for the system consisting out of the bullet and both blocks.  Here we use the latter approach.  The initial linear momentum of the system is just the linear momentum of the bullet:

 

 

To determine the final linear momentum we have to include the motion of both blocks:

 

 

Conservation of linear momentum requires that

 

 

or

 

 

 

Problem 13 (25 points)

a.     We apply conservation of mechanical energy to find the speed of the block at B.  Assuming the gravitational potential energy at B is 0 J, the gravitational potential energy at A is mgr.  Since the block starts from rest at A, the mechanical energy at A is just the potential energy and is thus equal to mgr.  At B, the potential energy is 0 J, and the mechanical energy is equal to the kinetic energy of the block.  Applying conservation of mechanical energy we find

 

 

or

 

 

 

b.     The normal force acting on the block between B and C is equal to mg.  The magnitude kinetic friction force acting on the block is thus equal to µkmg and the work done by the kinetic friction force when the block moves from B to C is equal to -µkmgL. 

 

c.     Applying the work-energy theorem we can not relate the change in the kinetic energy of the block to the work done by the friction force:

 

 

This equation can be rewritten, using the answer to part (a) as

 

 

We can now determine the velocity of the block at C:

 

 

 

d.     When the block hits the spring, the mechanical energy of the system is just equal to the kinetic energy of the block.  When the block comes to rest, all the kinetic energy of the block is transformed into potential energy of the spring.  Conservation of mechanical energy requires that

 

 

The spring constant k can now be determined from the known compression d: