Physics 121, Midterm Exam #2
Tuesday March 23, 2004
8.00 am – 9.30 am
Do not turn the pages of the exam until
you are instructed to do so.
You are responsible for reading the following rules
carefully before beginning.
Exam rules: You may use only a
writing instrument while taking this test. You may not consult
any calculators, computers, books, notes, or each other.
Procedure: Answer the multiple-choice questions (problems 1 – 10) by marking your answer on the scantron form. For each multiple-choice question (problems 1 – 10), select only one answer. Questions with more than one answer selected will be considered incorrect. Problems 11, 12, and 13 must be answered in the blue exam booklet and need to be well motivated and expressed in terms of the variables used in the problem. You will receive partial credit where appropriate, but only when we can read your solution. Answers that are not motivated will not receive any credit, even if correct.
At the end of the exam, you must
hand in the blue exam booklet and the scantron form. All items must be clearly labeled with your name and student
ID number. If any of these items
are missing, we will not grade your exam, and you will receive a score of 0
points.
Note: You are not
allowed to use a cheat sheet on this exam. Please refer to the formula sheet at the end of this package
for important equations.
Problem 1 (2.5 points)
Suppose the radius of the Earth was doubled while its density was kept fixed. The value of the gravitational acceleration at the surface would
c increase by a factor of 2.
c decrease by a factor of 2.
c remain the same.
Problem 2 (2.5 points)
The weight of an object in a cavern below the EarthÕs surface is
c greater than its weight at the surface.
c less than its weight at the surface.
c equal to its weight at the surface.
Problem 3 (2.5 points)
Two objects, each of mass m, are placed on the x axis, one at x = d and the other at x = -d. The gravitational force due to these two objects on an object located on the y axis takes on its maximum magnitude at
c y = 0
c y = ´
c y = ±d
c y = ±d/Ã2
Problem 4 (2.5 points)
A box (mass 5 kg) is accelerated by a force F across the floor with an acceleration of 2 m/s2 for 10 s. The work done by the force is
c 50 J
c 100 J
c 1000 J
c 1500 J
Problem 5 (2.5 points)
The work done by a force F = k |x| on an object moving along the x axis directly from x = -2 m to x = +2 m is
c 0 J
c 2k
c 4k
c 8k
Problem 6 (2.5 points)
What is the force that corresponds to the potential energy function U(x, y) = 3xy + 5x2 + 6y3?
c F = 5x2i + 6y3j
c F = 3xyi + 3xyj
c F = (-3y – 10x)i + (-3x – 18y2)j
c F = (3y + 10x)i + (-3x – 18y2)j
Problem 7 (2.5 points)
A ball is dropped from a height h and hits the ground with speed v. To have the ball hit the ground with a speed 2v it should be dropped from a height
c h
c 2h
c 3h
c 4h
Problem 8 (2.5 points)
Three uniform spheres of radii 2R, R, and 3R are placed in contact next to each other on the x axis in this order (the smallest sphere is in the center, the 2R sphere is located to the left, and the 3R sphere is located to the right). The centers of the spheres are located on the x axis. What is the distance from the center of mass of this system from the center of the smallest sphere, assuming that each sphere has the same density?
c (7/3)R
c (1/3)R
c (3/7)R
c (65/36)R
Problem 9 (2.5 points)
If the kinetic energy of an auto triples because of a speed change, its linear momentum
c increases by a factor of 3.
c remains the same.
c increases by a factor 9.
c increases by a factor of Ã3.
Problem 10 (2.5 points)
A tennis ball moving with a speed of 10 m/s collides elastically in a head-on collision with a massive locomotive engine moving with a speed of 10 m/s towards the ball. After bouncing directly back, the ball has a speed of
c 20 m/s.
c 30 m/s.
c 40 m/s.
Problem 11 (25 points)
Several planets (Jupiter, Uranus, Saturn) possess nearly circular surrounding rings, perhaps composed of material that failed to form a satellite. In addition, many galaxies contain ring-like structures. Consider a homogeneous ring of mass M and radius R.
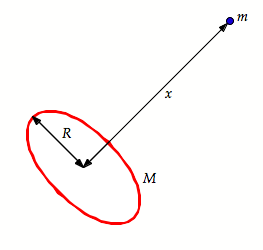
a. What is the direction of the gravitational force exerted by the ring on a particle of mass m located a distance x from the center of the ring along its axis (see Figure)?
b. What is the magnitude of the gravitational force exerted by the ring on the particle when it is located a distance x from the center of the ring along its axis?
c. What is the potential energy of mass m as a function of the distance x?
d. Suppose the particle falls from rest from its current distance x as a result of the attraction of the ring of matter. Find an expression for the speed with which it passes through the center of the ring. Note: assume that the ring remains stationary at all times.
Express all your answers in terms of x, R, m and M.
Problem 12 (25 points)
A bullet of mass m is fired horizontally at two blocks resting on a smooth frictionless table top, as shown in the Figure. The bullet passes through the first block of mass M1, and embeds itself in a second block of mass M2. Speeds equal to v1 and v2, respectively, are thereby imparted on the blocks, as shown in the Figure. The mass removed from the first block by the bullet can be neglected.

a. Find the speed of the bullet immediately after emerging from the first block.
b. Find the original speed v0 of the bullet.
Express your answers in term of M1, M2, v1, v2, and m.
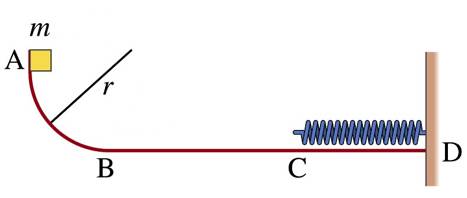
Problem 13 (25 points)