Physics 121, Midterm Exam #1

Tuesday February 17, 2004

8.00 am – 9.30 am

Do not turn the pages of the exam until you are instructed to do so.

You are responsible for reading the following rules carefully before beginning.

Exam rules: You may use only a writing instrument and your “cheat” sheet while taking this test. You may not consult any calculators, computers, books, nor each other.

Answer the multiple-choice questions (problems 1 – 10) by marking your answer on the attached pages. For each multiple-choice question (problems 1 – 10), select only one answer. Questions with more than one answer selected will be considered incorrect. Problems 11, 12, and 13 must be answered in the blue exam booklets and need to be well motivated and expressed in terms of the variables used in the problem. You will receive partial credit where appropriate, but only when we can read your solution. Answers that are not motivated will not receive any credit, even if correct.

At the end of the exam, you need to hand in your exam, the blue exam booklet, and your “cheat” sheet. All items must be clearly labeled with your name and student ID number. If any of these items is missing, we will not grade your exam, and you will receive a score of 0 points.

Name: __________________________________________________

ID number: ______________________________________________

Workshop Day/Time: ______________________________________

Useful Relations:

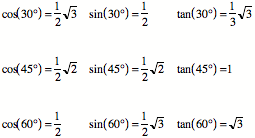
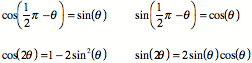
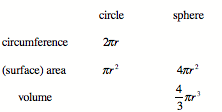
Problem 1 (2.5 points)

A ball is dropped from the edge of a cliff. Soon after, a second ball is dropped. As a function of time the separation between the two balls

c stays the same.

c increases.

c decreases.

c it depends on the time specified.

Problem 2 (2.5 points)

Which of the following statements is true for two balls thrown in the air with the same speed at different angles with the horizontal? Ignore air friction.

c The ball making the steeper angle spends more time in the air.

c The ball making the shallower angle spends more time in the air.

c The time of flight depends only on the initial speed given to each ball.

Problem 3 (2.5 points)

Two balls are projected off a cliff. One is thrown horizontally while the other is released from rest and falls vertically. Which of the following statements is true?

c The ball that falls vertically hits the ground first.

c The ball that is projected horizontally hits the ground first.

c Both balls hit the ground at the same time.

c We can not determine which ball hits the ground first unless we know the speed at which the first ball was projected horizontally.

Problem 4 (2.5 points)

An elevator has a frayed cable which will break if the tension exceeds a certain value. The tension more likely to exceed this value if the elevator is

c moving at constant velocity.

c accelerating upward.

c accelerating downward.

c the motion is irrelevant.

Problem 5 (2.5 points)

Two blocks of the same size but different masses, m₁ and m₂, are placed on a table side-by-side in contact with each other. Assume that m₁ > m₂. Let N₁ be the normal force between the two blocks when you push horizontally on the free side of m₁ (towards m₂). Let N₂ be the normal force between the two blocks when you push horizontally on the free side of m₂ (towards m₁). Which of the following statements is true?

c N₁ = N₂

c N₁ < N₂

c N₁ > N₂

Problem 6 (2.5 points)

A horizontal force measured with a spring scale is applied to a box sitting on a table. Until the force is increased to a particular value the box does not move. Just as the box starts moving the reading on the spring scale

c remains the same.

c decreases.

c increases.

c more information is needed.

Problem 7 (2.5 points)

A skier accelerates down a slope inclined at an angle q. From this information we conclude that

c m_k > tanq

c m_k > tanq

c m_k = tanq

c m_k = m_s

Problem 8 (2.5 points)

A stunt car goes around a loop-the-loop, hanging upside down at the top. The car does not fall because

c there is a downward force on the car.

c there is an upward force on the car.

c there is a sideways force on the car.

Problem 9 (2.5 points)

A ball slides down an inclined track and then rounds a loop-the-loop. The ball is released from an initial height so that it has just enough speed to go around the loop without falling off. At the top of the loop-the-loop the normal force of the loop on the ball is

c equal to the weight of the ball and pointing down.

c equal to the weight of the ball and pointing up.

c equal to twice the weight of the ball and point up.

c equal to zero.

Problem 10 (2.5 points)

The time it takes a falling object to attain its terminal velocity

c increases with increasing mass.

c decreases with increasing mass.

c is independent of mass.

Problem 11 (25 points)

Consider three blocks with masses M₁, M₂, and M₃, arranged as shown in the Figure below. An external force F is applied to the large block (M₃) so that mass M₁ does not move with respect to mass M₃. Ignore all forms of friction.

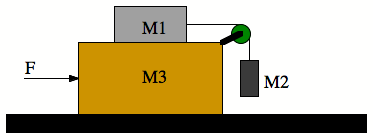
1. What is the acceleration of mass M₃? Express your answer in terms of the external force F and the masses M₁, M₂, and M₃.
2. What is the net force on mass M₁? Express your answer in terms of the external force F and the masses M₁, M₂, and M₃.
3. What must be the magnitude of the external force F in order to ensure that mass M₁ does not move with respect to mass M₃? Express your answer in terms of the masses M₁, M₂, and M₃.
4. What will happen to the position of mass M₁ with respect to the position of mass M₃ when the magnitude of the external force is smaller than the value calculated in (c)? What will happen to the position of mass M₁ with respect to the position of mass M₃ when the magnitude of the external force is larger than the magnitude of the force calculated in (c)?

Problem 12 (25 points)

A sphere of mass M is attached with a string of length L to a rod. The sphere is carrying out a circular motion around the rod. When the sphere has a speed v, the angle between the string and the horizontal plane is q and constant. The height of the sphere above the ground is h.

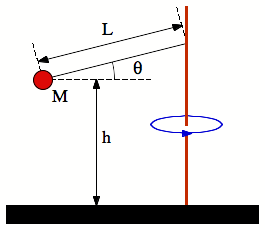
1. What is the horizontal component of the net force acting on the sphere? Specify both magnitude and direction. Express your answer in terms of v, L, M, and q.
2. What is the vertical component of the net force acting on the sphere? Specify both magnitude and direction. Express your answer in terms of v, L, M, and q.
3. Use the answer to (a) to express the tension T in the string in terms of v, L, M, and q. Also, use the answer to (b) to express the tension T in the string in terms of v, L, M, and q.
4. Use the two expressions for the tension obtained in (c) the find a relation between v and q and use this relation to determine what happens to q when v increases. What happens to q when M increases?
5. At one point in time, the string breaks. How long after the string breaks will the sphere hit the ground? Express your answer in terms of h, v, L, M, and q.

Problem 13 (25 points)

Two blocks, made of different materials, are connected together by a thin cord. They slide down a ramp include at an angle q to the horizontal as shown in the Figure below. The lower block has a mass m₁ and the upper block has a mass m₂. The coefficients of static and kinetic friction between the blocks and the ramp are m_s and m_k, respectively.

a. What is the normal force acting on block 1? Express your answer in terms of m₁, m₂, q, m_s and m_k.

b. What is the normal force acting on block 2? Express your answer in terms of m₁, m₂, q, m_s and m_k.

c. What is the acceleration of block 1? Express your answer in terms of m₁, m₂, q, m_s and m_k.

d. What is the tension in the cord? Express your answer in terms of m₁, m₂, q, m_s and m_k.