17. Heat and the First Law of Thermodynamics
17.1. Heat
Two bodies brought in thermal contact will change their temperature until they are at the same temperature. In the process of reaching thermal equilibrium, heat is transferred from one body to the other.
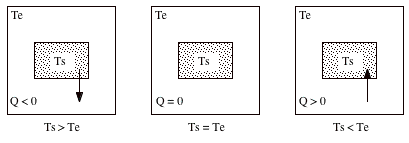
Suppose we have a system of interest at temperature TS surrounded by an environment with temperature TE. If TS > TE heat flows from the system to the environment. If TS < TE heat flows from the environment into the system. Heat, presented by the symbol Q and unit Joule, is chosen to be positive when heat flows into the system, and negative if heat flows out of the system (see Figure 17.1). Heat flow is a results of a temperature difference between two bodies, and the flow of heat is zero if TS = TE.
|
Figure 17.1. Heat Flow. |
Heat is not the only way in which energy can be transferred between a system and its environment. Energy can also be transferred between a system and its environment by means of work (W). The unit of work is the Joule.
Another commonly used unit is the calorie. The calorie is defined as the amount of heat that would raise the temperature of 1 g of water from 14.5 ˇC to 15.5 ˇC. The Joule and the calorie are related as follows: 1 cal = 4.1860 J
17.2. Heat Capacity
When heat is added to an object, its temperature increases. The change in the temperature is proportional to the amount of heat added
![]()
The constant C is called the heat capacity of the object. The heat capacity of an object depends on its mass and the type of material of which it is made. The heat capacity of an object is proportional to its mass, and the heat capacity per unit mass, c, is commonly used. In that case
![]()
where m is the mass of the object. The molar heat capacity is the heat capacity per mole of material. For most materials the molar heat capacity is 25 J/mol K.
In order to determine the heat capacity of a substance we not only need to know how much heat is added, but also the conditions under which the heat transfer took place. For gases, adding heat under constant pressure and under constant temperature will lead to very different values of the specific heat capacity.
17.3. Heat of Transformation
When heat is added to a solid or a liquid, the temperature of the sample does not necessarily rise. During a phase change (melting, boiling) heat is added to the sample without an increase in temperature. The amount of heat transferred per mass unit during a phase change is called the heat of transformation (symbol L) for the process. The amount of heat needed/released is given by
![]()
where m is the mass of the sample.
Problem 28P
What mass of steam of 100ˇC must be mixed with 150 g of ice at 0ˇC, in a thermally insulated container, to produce liquid water at 50ˇC ?
We start with calculating the heat required to transform 150 g of ice at 0ˇC to 150 g of liquid at 0ˇC. The heat of transformation of water is 333 kJ/kg (see Table 20-2, page 555). The transformation of ice into water therefore requires a total heat given by
![]()
The heat required to change the temperature of 150 g of water from 0ˇC to 50ˇC is given by
![]()
The total heat that needs to be added to the system is therefore equal to 81.5 kJ. This heat must be supplied by the steam. Heat will be released when the steam is transformed into liquid, The heat of transformation for this process is 2260 kJ/kg. Suppose the mass of the steam is m. The total heat released in the conversion of steam into water is given by
![]()
The heat released when the steam cools down from 100ˇC to 50ˇC is given by
![]()
The total heat released by the cooling of the steam is therefore equal to 2470 m kJ. The total heat required is 81.5 kJ, and we therefore conclude that the mass of the steam must be equal to 33 g.
17.4. Work
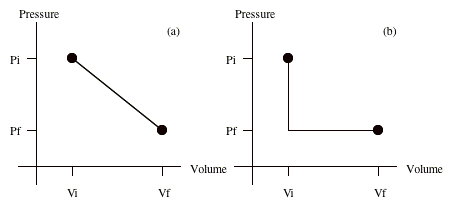
Suppose a system starts from an initial state described by a pressure pi, a volume Vi, and a temperature Ti. The final state of the system is described by a pressure pf, a volume Vf, and a temperature Tf. The transformation from the initial state to the final state can be achieved in a variety of ways (see for example Figure 17.2). In Figure 17.2a both pressure and volume change simultaneously. In Figure 17.2b the pressure of the system is first lowered while keeping the volume constant (this can for example be achieved by cooling the sample) and subsequently, the volume is increased while keeping the pressure constant (this can be achieved by heating the gas while increasing the volume).
If the pressure of a gas increases it can move a piston (this happens in an engine). In this case, work is done by the system as the expanding gas lifts the piston. On the other hand, if we increase the weight of the piston, work will be done on the system as the piston falls. The force exerted by the gas on the piston is equal to p A, where A is the area of the piston and p is the gas pressure. If the piston is displaced by a distance ds, the amount of work done can be calculated as follows:
![]()
|
Figure 17.2. Two possible ways to get from the initial state to the final state. |
The total work done during a finite displacement of the piston is now easy to calculate
![]()
If W is positive, work was done by the system (for example, the expanding gas lifts the piston). A negative value of W tells you that work was done on the system (the piston is pressed down in order to compress the gas).
The amount of work done is equal to the area under the curve in the pV diagrams shown in Figure 17.2. Clearly, the amount of work done depends on the path chosen. The work W for the path shown in Figure 17.2a is significantly more than the work W for the path shown in Figure 17.2b. Any change in the system in which the volume does not change will not produce/cost any work. The work done for the paths shown in Figure 17.2 can be calculated easily
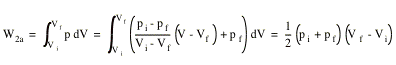
No work is done for the path shown in Figure 17.2b between (pi, Vi) and (pf, Vi) since there is no change in volume. The work done to move from (pf, Vi) to (pf, Vf) is calculated easily
![]()
Clearly, W2b is always less then W2a, and we can make the amount of work done as small or as large as we want. For example no work would be done if the transition follows the following path:
(pi, Vi) ¨ (0, Vi) ¨ (0, Vf) ¨ (pf, Vi)
A system can be taken from a given initial state to a given final state by an infinite number of processes. In general, the work W and also the heat Q will have different values for each of these processes. We say that heat and work are path-dependent quantities.
From the previous discussion neither Q nor W represents a change in some intrinsic properties of the system. Experimentally, however, it is observed that the quantity Q - W is the same for all processes. It depends only on the initial and final states and it does not matter at what path is followed to get from one to the other. The quantity Q - W is called the change in the internal energy U of the system:
ĆU = Uf - Ui = Q - W
This equation is called the first law of thermodynamics. For small changes the first law of thermodynamics can be rewritten as
dU = dQ - dW
17.4.1. Adiabatic Processes
If a system is well insulated, no transfer of heat will occur between it and its environment. This means that Q = 0, and the first law of thermodynamics shows that
ĆU = - W
If work is done by the system (positive W) its internal energy decreases. Conversely, if work is done on the system (negative W) its internal energy will increase. For gases, the internal energy is related to the temperature: a higher internal energy means a higher temperature. Adiabatic expansion of a gas will lower its temperature; adiabatic compression of a gas will increase its temperature.
17.4.2. Constant Volume Processes
If the volume of a system is held constant, the system can do no work (W = 0 J). The first law of thermodynamics then shows that
ĆU = Q
If heat is added to the system its internal energy will increase; if heat is removed from the system its internal energy will decrease.
17.4.3. Cyclical Processes
Processes which, after certain interchanges of heat and work, are restored to their initial state are called cyclical processes. In this case, no intrinsic properties of the system are changed, and therefore ĆU = 0. The first law of thermodynamics now immediately yields
Q = W
17.4.4. Free Expansion
Free expansion is an adiabatic process in which no work is done on or by the system. This means that Q = W = 0 J, and the first law of thermodynamics now requires that
ĆU = 0 J
17.5. Transfer of Heat
The transfer of heat between a system and its environment can occur in a variety of ways. Three different mechanisms of heat transfer will now be discussed: conduction, convection, and radiation.
17.5.1. Conduction
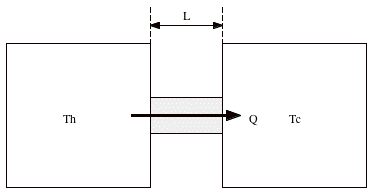
Consider the slab of material shown in Figure 17.3. The left end of the beam is maintained at a temperature TH; the right end of the beam is maintained at a temperature TC. As a result of the temperature difference heat will flow through the slab, from its hot end to its cold end. Experimentally it is shown that the rate of heat transfer (Q/t) is proportional to the cross-sectional area of the slab, proportional to the temperature difference, and inversely proportional to the length of the slab
![]()
Here, k is the thermal conductivity, which is a constant that depends on the type of material. Large values of k define good heat conductors. The thermal resistance R is related to the thermal conductivity k in the following manner
![]()
|
Figure 17.3. Conduction. |
Thus, the lower the thermal conductivity of the material, the higher the thermal resistance R. From the definition of R it immediately follows that
![]()
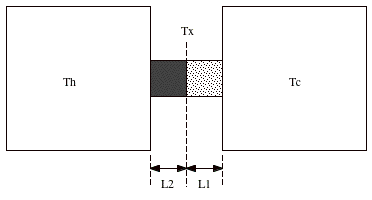
Consider a composite slab is made up out of two different materials, with length L1 and L2, and with thermal conductivity k1 and k2, is placed between two heat baths (see Figure 17.4). Suppose that the temperature of the interface between the two slabs is equal to Tx. The amount of heat flowing from TH to Tx is given by
![]()
The amount of heat flowing from Tx to TC is given by
![]()
Of course, the heat flowing through slab 1 must equal the heat flowing through slab 2. Thus
![]()
|
Figure 17.4. Heat transport through a composite slab. |
This equation can be used to obtain the temperature at the interface between slab 1 and slab 2:
![]()
The heat flowing through the slab can now be calculated easily
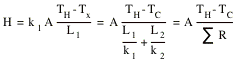
A composite slab therefore has a thermal resistance equal to the sum of the thermal resistance of each of the individual slabs.
17.5.2. Convection
Heat transfer by convection occurs when a fluid, such as air or water, is in contact with an object whose temperature is higher than the temperature of its surroundings. The temperature of the fluid increases and (in most cases) the fluid expands. Being less dense than the surrounding cooler fluid, it rises because of buoyant forces. The surrounding cooler fluid falls to take the place of the rising warmer fluid and a convective circulation is set up.
17.5.3. Radiation
Every object emits electromagnetic radiation. The energy spectrum of the radiation emitted depends on the temperature of the object; the average energy increases with increasing temperature.
Problem 57P
A container of water has been outdoors in cold weather until a 5.0 cm-thick slab of ice has formed on its surface. The air above the ice is at -10ˇC. Calculate the rate of formation of ice (in centimeters per hour) on the bottom surface of the ice slab. Take the thermal conductivity of ice to be 0.0040 cal/s . cm . ˇC and the density to be 0.92 g/cm3.
The water at the boundary between the water and the ice will be at a temperature of 0ˇC. The heat transported through 5 cm of ice is equal to
![]()
This heat is released when water is transformed into ice. The heat of transformation of this process is 79.5 cal/g. Suppose a mass m of water is transformed each second into ice. This produces a total heat equal to
H = 79.5 m cal/s
This must be equal to the heat flow through the ice:
79.5 m = 0.0080 A
A mass m of ice (covering an area A) will have a thickness d, where d is given by
![]()
Combining the last two expression we obtain for the rate of ice formation:
![]()