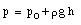
Thermodynamics deals with the internal energies of systems and is governed by a set of laws (similar to Newton's law for mechanics). The central concept of thermodynamics is the temperature T. Properties of many bodies change as their thermal environment is altered. When the temperature increases, the volume of a liquid increases, the length of a metal rod increases, the electrical resistance increases, the pressure of a confined gas increases, etc. If we know the change in these parameters as a function of the temperature, we can use them to measure the temperature. The device is then called a thermometer.
In order for a thermometer to measure the temperature of a body, it must be in intimate contact with the body. After making contact, every measurable property of the thermometer and the body assumes a stable value, and the bodies are said to be in thermal equilibrium. If the thermometer is also in thermal equilibrium with a second body than the two bodies are also in thermal equilibrium. This is called the zeroth law of thermodynamics. The temperature is a property of a body, and two bodies are found to be in thermal equilibrium if their temperatures are equal.
The first step in defining a temperature scale is to pick out some reproducible thermal environment and, quit arbitrarily, assign a certain temperature to it. The unit of temperature will be the Kelvin. The reference point is the triple point of water. Ice, water and vapor can only coexist at one temperature and pressure. The triple point of water has been assigned a temperature of 273.16 K. Water can boil or freeze at different temperatures (depending on the pressure) and therefore boiling or freezing of water can not be used to define a standard temperature.
The standard thermometer, against which all other thermometers are to be calibrated, is based on the pressure exerted by a gas confined to a fixed volume. This device is called the constant volume gas thermometer, see Figure 16.1). It consists of a bulb connected by a capillary tube to a manometer. The bulb is filled with a gas and in thermal contact with the body whose temperature is to be measured. A reservoir of mercury is raised or lowered such that the volume of the gas in the bulb remains constant. The pressure of the gas in the bulb can be obtained by measuring the level difference h of the manometer
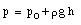
where p0 is the atmospheric pressure and [[rho]] is the density of mercury in the manometer. The temperature of the body is defined as
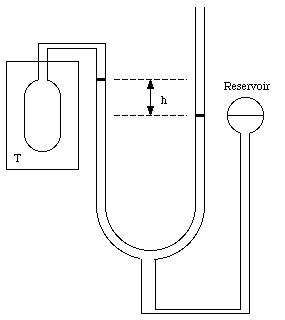
Figure 16.1. The constant volume gas thermometer.
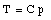
where C is a constant. In a similar fashion we can measure the temperature of the triple point cell in order to obtain our reference temperature:
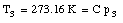
Combining the two measurements we obtain for T
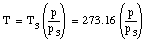
The temperature obtained in this manner will depend slightly on the amount and the type of gas in the bulb. However, if smaller and smaller amounts of the gas are used, the measured temperature converges for different gasses.
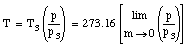
Therefore, the temperature obtained by extrapolating the measured temperatures to the case of no gas in the bulb is a temperature that does not depend on the specific properties of the materials involved. This temperature is a truly fundamental physical quantity, whose definition is independent of the properties of the specific materials.
The Kelvin scale is the unit to be used in basic scientific work. In most countries, the Celsius scale or the Fahrenheit scale is used to express the temperature for popular and commercial use. The Celsius temperature, TC, is related to the Kelvin scale in the following manner
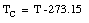
For example,
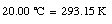
The Fahrenheit temperature, TF, is related to the Celsius scale in the following manner
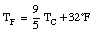
For example,
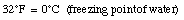
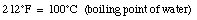
When the temperature of a material increases its length increases. This effect is called thermal expansion. The increase in length, [[Delta]]L, is proportional to the change in temperature [[Delta]]T:
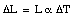
where [[alpha]] is a constant called the coefficient of linear expansion. The coefficient of linear expansion depends on the material and typical values range between 0.5 x 10-6 K-1 and 10 x 10-6 K-1 (at room temperature).
For liquids the volume expansion is the only meaningful parameter
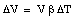
where [[beta]] is the coefficient of volume expansion for the liquid. The coefficients of volume expansion and linear expansion are related. Suppose the temperature of a volume V (length L, height H and width W) is increased by [[Delta]]T. The volume change [[Delta]]V can be calculated
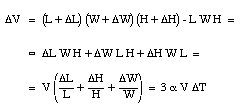
We conclude that
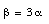
Water is the only exception of simple thermal expansion. Its specific volume passes through a minimum (maximum density) at 4 deg.C. Between 0 deg.C and 4 deg.C the water contracts with increasing temperature, and above 4 deg.C it expands with increasing temperature (that is why water pipes burst when they freeze).
NOTE: The atoms in a solid are held together in a three-dimensional periodic lattice by spring-like interaction forces. The potential energy for a pair of neighboring atoms depends on their separation r, and has a minimum at r = r0. The distance r0 is the lattice spacing of a solid when the temperature approaches zero. The potential energy curve is not symmetrical around r = r0; it rises more steeply when the atoms are pushed together (r < r0) than when they are pulled apart (r > r0). The average separation distance at a temperature above the absolute zero will therefore be larger than r0. A solid with a symmetric potential energy curve would not expand.
Example - Problem 41P
Show that when the temperature in a liquid in a barometer changes by [[Delta]]T, and the pressure is constant, the height h changes by [[Delta]]h = [[beta]] h [[Delta]]T, where [[beta]] is the coefficient of volume expansion. Neglect the expansion of the glass tube.
Suppose the cross-sectional area of the glass tube is A and the original height of the liquid is h. The volume of the liquid is equal to
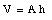
Due to the change in temperature [[Delta]]T the volume of the liquid will change by [[Delta]]V
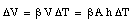
Assuming that the cross section A remains constant (no expansion of glass) we can conclude that
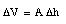
and therefore
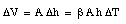
Thus
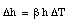
The operation of a mercury thermometer is based on the volume expansion of mercury. Suppose a volume V of mercury is brought in thermal contacts with a body. As a result, the temperature of the mercury will change by [[Delta]]T. Its volume will change by [[Delta]]V
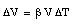
The mercury is contained in an evacuated system which does not change size as a result of the change in temperature. Connected to the reservoir is a thin glass tube which serves as the expansion volume for the mercury. The glass tube has an area equal to A, and the change in the height h of the mercury level in the tube is determined by the change in volume [[Delta]]V
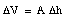
We conclude that
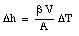
Thus, by measuring the change in the height of the mercury column we can measure the change in the temperature of the mercury.