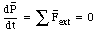
An object is in equilibrium if the linear momentum of its center of mass is constant and if its angular momentum about its center of mass is constant:
P = constant
L = constant
An object is in static equilibrium if its linear momentum and angular momentum is equal to zero:
P = 0 kg m/s
L = 0 kg m2/s
If a body is in translational equilibrium then dP/dt = 0, or
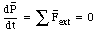
If a body is in rotational equilibrium then dL/dt = 0, or
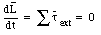
In summary, the following equations must be satisfied for an object in static equilibrium
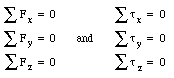
If we restrict ourselves to two dimensions (the x-y plane) the following equations must be satisfied:
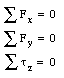
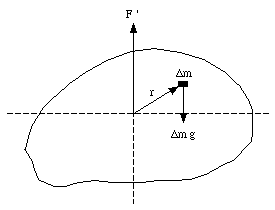
Figure 13.1. Weight of an object balanced by a single force.
Figure 13.1 shows a body of arbitrary shape balanced by a single force. The origin of the coordinate system is defined such that it coincides with the center of gravity of the object, which is the point upon which the balancing force acts. An object that is supported at its center of gravity will be in static equilibrium, independent of the orientation of the object. If the body is in equilibrium, the net force acting on it must be zero. Figure 13.1 shows that
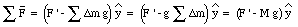
Since the body is in equilibrium
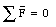
and therefore
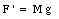
In obtaining this result we have assumed that the gravitational acceleration is the same for every point of the body. The net torque acting on the body is given by
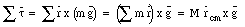
Since the body is in static equilibrium
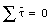
and therefore
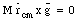
This shows that rcm = 0 or rcm is parallel to g. We conclude that for a body to be in equilibrium, its center of mass must coincide with its center of gravity.
Sample Problem 13-1
A uniform beam of length L whose mass is m, rest with its ends on two digital scales (see Figure 13.2). A block whose mass is M rests on the beam, its center one-fourth away from the beam's left end. What do the scales read ?
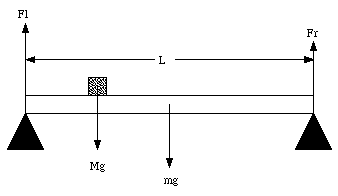
Figure 13.2. Sample problem 13-1.
For the system to be in equilibrium, the net force and net torque must be zero. Figure 13.2 shows that
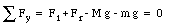
Here we have replaced the force acting on the beam with a single force acting on its center of gravity. The net torque of the system, with respect to the left scale, is
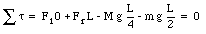
This shows immediately that
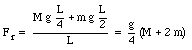
From the equation of the net force we obtain
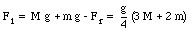
Sample Problem 13-3
A ladder with length L and mass m rests against a wall. Its upper end is a distance h above the ground (see Figure 13.3). The center of gravity of the ladder is one-third of the way up the ladder. A firefighter with mass M climbs halfway up the ladder. Assume that the wall, but not the ground, is frictionless. What is the force exerted on the ladder by the wall and by the ground ?
The wall exerts a horizontal force FW on the ladder (the normal force); it exerts no vertical force. The ground exerts a force Fg on the ladder with a horizontal component Fgx and a vertical component Fgy. If these two components were not present, the system would not be in equilibrium. The net force in the x and y directions is given by
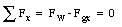
and
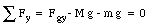
The net torque, with respect to O (which is the contact point between the ladder and the ground), is given by
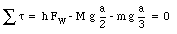
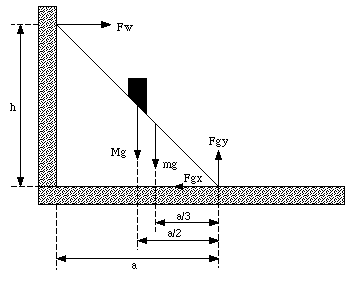
Figure 13.3. Sample Problem 13-3
This immediately shows that
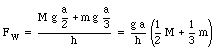
We can now calculate the force Fg:
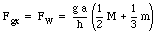
and
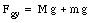
We observe that Fgx depends on the position of the firefighter. Suppose that the firefighter is a distance f L up the ladder. In this case Fgx is given by
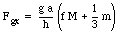
If the coefficient of static friction between the ladder and the ground is us, than the maximum distance the firefighter can climb is reached when
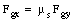
or
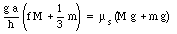
This shows that
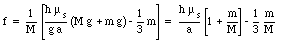
Two bricks of length L and mass m are stacked. Using conditions of static equilibrium we can determine the maximum overhang of the top brick (see Figure 13.4).
The two forces acting on the top brick are the gravitational force Fg and the normal force N, exerted by the bottom brick on the top brick. Both forces are directed along the y-axis. Since the system is in equilibrium, the net force acting along the y-axis must be zero. We conclude that
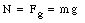
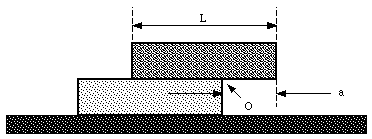
Figure 13.4. Two stacked bricks.
If the top block is on the verge of falling down, it will rotate around O. The torque exerted by the two external forces with respect to O can be easily calculated (see Figure 13.5). The gravitational force Fg acting on the whole block is replaced by a single force with magnitude m g acting on the center of mass of the top block. The normal force N acting on the whole contact area between the top and the bottom block is replaced by a single force N acting on a point a distance d away from the rotation axis O. The torque of the normal force and the gravitational force with respect to O is given by
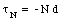
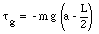
The net torque acting on the top brick is given by
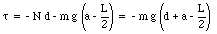
If the system is in equilibrium, then the net torque acting on the top brick with respect to O must be zero. This implies that
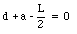
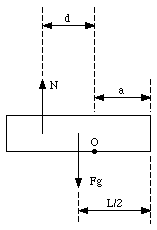
Figure 13.5. Forces acting on top brick.
or
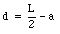
This equation shows that the system can never be in equilibrium if a > L/2 (since d < 0 in that case). The system will be on the verge of losing equilibrium if a = L/2. In this case, d = 0. We conclude that the system can not be in equilibrium if the center of mass of the top brick is located to the right of the edge of the bottom brick. the system will be on the verge of losing equilibrium if the center of mass of the top brick is located right over the edge of the bottom brick. Finally, if the center of mass of the top brick is located to the left of the edge of the bottom brick, the system will be in equilibrium.