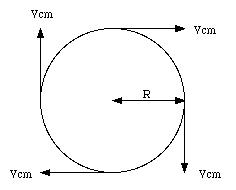

Figure 12.1. Rotational Motion of Wheel
A wheel rolling over a surface has both a linear and a rotational velocity. Suppose the angular velocity of the wheel is [omega]. The corresponding linear velocity of any point on the rim of the wheel is given by
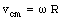
where R is the radius of the wheel (see Figure 12.1). When the wheel is in contact with the ground, its bottom part is at rest with respect to the ground. This implies that besides a rotational motion the wheel experiences a linear motion with a velocity equal to + vcm (see Figure 12.2). We conclude that the top of the wheel moves twice as fast as the center and the bottom of the wheel does not move at all.
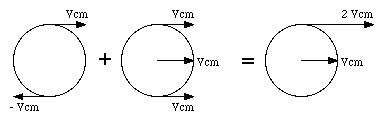
Figure 12.2. Motion of wheel is sum of rotational and translational motion.
An alternative way of looking at the motion of a wheel is by regarding it as a pure rotation (with the same angular velocity [omega]) about an instantaneous stationary axis through the bottom of the wheel (point P, Figure 12.3).
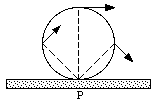
Figure 12.3. Motion of wheel around axis through P.
The kinetic energy of the wheel shown in Figure 12.3 can be calculated easily using the formulas derived in Chapter 11
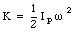
where IP is the rotational inertia around the axis through P, and [omega] is the rotational velocity of the wheel. The rotational inertia around an axis through P, IP, is related to the rotational inertia around an axis through the center of mass, Icm
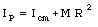
The kinetic energy of the wheel can now be rewritten as
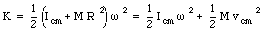
where the first term is the kinetic energy associated with the rotation of the wheel about an axis through its center of mass and the second term is associated with the translational motion of the wheel.
Example Problem 12-1
Figure 12.4 shows a disk with mass M and rotational inertia I on an inclined plane. The mass is released from a height h. What is its final velocity at the bottom of the plane ?
The disk is released from rest. Its total mechanical energy at that point is equal to its potential energy
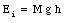
When the disk reaches the bottom of the plane, all of its potential energy is converted into kinetic energy. The kinetic energy of the disk will consist out of rotational and translational kinetic energy:
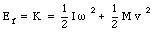
The moment of inertia of the disk is given by
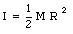
where R is the radius of the disk. The kinetic energy of the disk can now be rewritten as
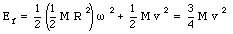
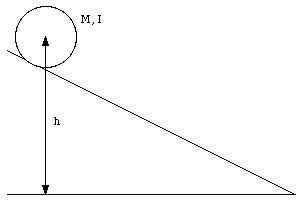
Figure 12.4. Mass on inclined plane.
Conservation of mechanical energy implies that Ei = Ef, or
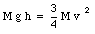
This shows that the velocity of the disk is given by
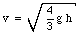
Consider now two different disks with identical mass M but different moments of inertia. In this case the final kinetic energy can be written as
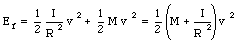
Conservation of energy now requires that
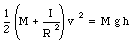
or
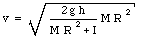
We conclude that in this case, the disk with the smallest moment of inertia has the largest final velocity.
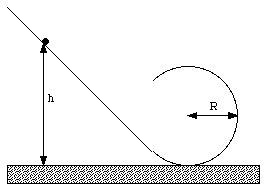
Figure 12.5. Problem 13P.
Problem 15P
A small solid marble of mass m and radius r rolls without slipping along a loop-the-loop track shown in Figure 12.5, having been released from rest somewhere along the straight section of the track. From what minimum height above the bottom of the track must the marble be released in order not to leave the track at the top of the loop.
The marble will not leave the track at the top of the loop if the centripetal force exceeds the gravitational force at that point:
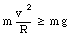
or
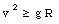
The kinetic energy of the marble at the top consists out of rotational and translational energy
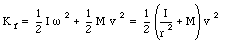
where we assumed that the marble is rolling over the track (no slipping). The moment of inertia of the marble is given by
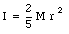
Using this expression we obtain for the kinetic energy
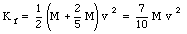
The marble will reach the top if
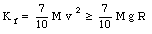
The total mechanical energy of the marble at the top of the loop-the-loop is equal to
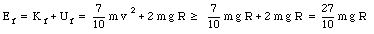
The initial energy of the marble is just its potential energy at a height h
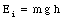
Conservation of energy now implies that
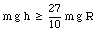
or
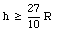
Example Problem 12-2: the yo-yo
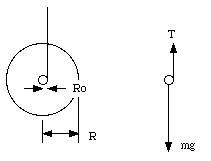
Figure 12.6. The yo-yo.
Figure 12.6 shows a schematic drawing of a yo-yo. What is its linear acceleration ?
There are two forces acting on the yo-yo: an upward force equal to the tension in the cord, and the gravitational force. The acceleration of the system depends on these two forces:
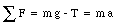
The rotational motion of the yo-yo is determined by the torque exerted by the tension T (the torque due to the gravitational force is zero)
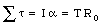
The rotational acceleration a is related to the linear acceleration a:
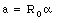
We can now write down the following equations for the tension T
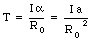
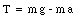
The linear acceleration a can now be calculated
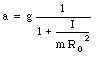
Thus, the yo-yo rolls down the string with a constant acceleration. The acceleration can be made smaller by increasing the rotational inertia and by decreasing the radius of the axle.
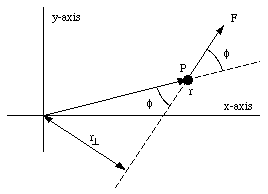
Figure 12.7. Motion of particle P in the x-y plane.
A particle with mass m moves in the x-y plane (see Figure 12.7). A single force F acts on the particle and the angle between the force and the position vector is [phi]. Per definition, the torque exerted by this force on the mass, with respect to the origin of our coordinate system, is given by
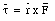
and
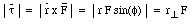
where r[invtee] is called the arm of the force F with respect to the origin. According to the definition of the vector product, the vector [tau] lies parallel to the z-axis, and its direction (either up or down) can be determined using the right-hand rule. Torque defined in this way has meaning only with respect to a specified origin. The direction of the torque is always at right angles to the plane formed by the vectors r and F. The torque is zero if r = 0 m, F = 0 N or r is parallel or anti-parallel to F.
The angular momentum L of particle P in Figure 12.7, with respect to the origin, is defined as
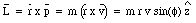
This definition implies that if the particle is moving directly away from the origin, or directly towards it, the angular momentum associated with this motion is zero. A particle will have a different angular momentum if the origin is chosen at a different location. A particle moving in a circle will have an angular momentum (with respect to the center of the circle) equal to
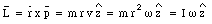
Again we notice the similarity between the definition of linear momentum and the definition of angular momentum.
A particle can have angular momentum even if it does not move in a circle. For example, Figure 12.8 shows the location and the direction of the momentum of particle P. The angular momentum of particle P, with respect to the origin, is given by
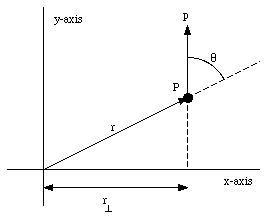
Figure 12.8. Angular momentum of particle P.
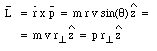
The change in the angular momentum of the particle can be obtained by differentiating the equation for l with respect to time
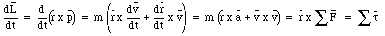
We conclude that
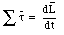
This equation shows that if the net torque acting on the particle is zero, its angular momentum will be constant.
Example Problem 12-3
Figure 12.9 shows object P in free fall. The object starts from rest at the position indicated in Figure 12.9. What is its angular momentum, with respect to the origin, as function of time ?
The velocity of object P, as function of time, is given by
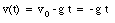
The angular momentum of object P is given by
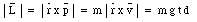
Therefore
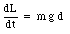
which is equal to the torque of the gravitational force with respect to the origin.
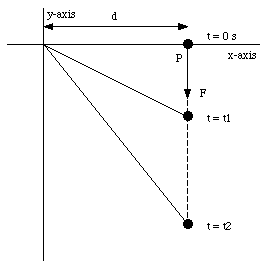
Figure 12.9. Free fall and angular momentum
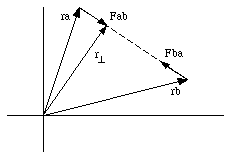
Figure 12.10. Action - reaction pair.
If we look at a system of particles, the total angular momentum L of the system is the vector sum of the angular momenta of each of the individual particles:
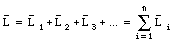
The change in the total angular momentum L is related to the change in the angular momentum of the individual particles
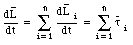
Some of the torques are internal, some are external. The internal torques come in pairs, and the vector sum of these is zero. This is illustrated in Figure 12.10. Figure 12.10 shows the particles A and B which interact via a central force. Newton's third law states that forces come in pairs: if B exerts a force FAB on A, than A will exert a force FBA on B. FAB and FBA are related as follows
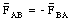
The torque exerted by each of these forces, with respect to the origin, can be easily calculated
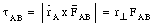
and
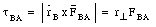
Clearly, these two torques add up to zero
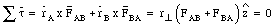
The net torque for each action-reaction pair, with respect to the origin, is equal to zero.
We conclude that
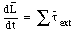
This equation is another way of expressing Newton's second law in angular quantities.
Suppose we are dealing with a rigid body rotating around the z-axis. The linear momentum of each mass element is parallel to the x-y plane, and perpendicular to the position vector. The magnitude of the angular momentum of this mass element is
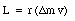
The z-component of this angular momentum is given by
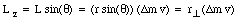
The z-component of the total angular momentum L of the rigid body can be obtained by summing over all mass elements in the body
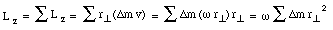
From the definition of the rotational inertia of the rigid body we can conclude that
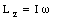
This is the projection of the total angular momentum onto the rotation axis. The rotational inertia I in this equation must also be calculated with respect to the same rotation axis. Only if the rotation axis is a symmetry axis of the rigid body will the total angular momentum vector coincide with the rotation axis.
If no external forces act on a system of particles or if the external torque is equal to zero, the total angular momentum of the system is conserved. The angular momentum remains constant, no matter what changes take place within the system.
Problem 54E
The rotational inertia of a collapsing spinning star changes to one-third of its initial value. What is the ratio of the new rotational kinetic energy to the initial rotational kinetic energy ?
The final rotational inertia If is related to the initial rotational inertia Ii as follows
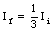
No external forces act on the system, and the total angular momentum is conserved
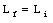
The initial rotational kinetic energy is given by
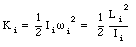
The final rotational kinetic energy is given by
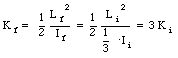
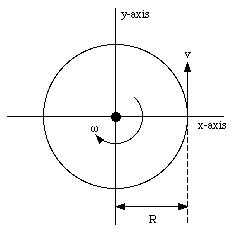
Figure 12.11. Problem 61P.
Problem 61P
A cockroach with mass m runs counterclockwise around the rim of a lazy Susan (a circular dish mounted on a vertical axle) of radius R and rotational inertia I with frictionless bearings. The cockroach's speed (with respect to the earth) is v, whereas the lazy Susan turns clockwise with angular speed [omega]0. The cockroach finds a bread crumb on the rim and, of course, stops. (a) What is the angular speed of the lazy Susan after the cockroach stops ? (b) Is mechanical energy conserved ?
Assume that the lazy Susan is located in the x-y plane (see Figure 12.11). The linear momentum of the cockroach is m . v. The angular momentum of the cockroach, with respect to the origin, is given by
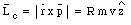
The direction of the angular momentum can be found using the right-hand rule. The direction of the z-axis is chosen such that the angular momentum of the cockroach coincides with the positive z-axis. The lazy Susan is moving clockwise (see Figure 12.11) and its angular momentum is pointing along the negative z-axis. Its angular momentum is given by
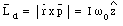
where I is the rotational inertia of the dish. Note that since the rotation is clockwise, [omega]0 is less than zero. The total angular momentum of the system is given by
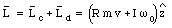
The rotational inertia of the dish plus cockroach is given by
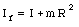
Since the external torque acting on the system is zero, the total angular momentum is conserved. The rotational velocity of the system after the cockroach stops is given by
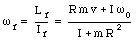
The initial kinetic energy of the system is equal to
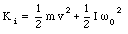
The final kinetic energy of the system is equal to
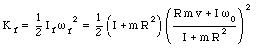
The change in kinetic energy of the system is
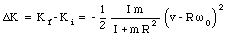
The change in the kinetic energy of the system is negative, and we conclude that mechanical energy is not conserved. The loss of mechanical energy is due to the work done by the friction force between the surface of the lazy Susan and the legs of the cockroach.
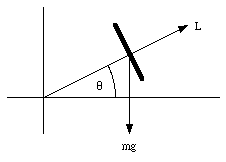
Figure 12.12. The precessing top.
A top, set spinning, will rotate slowly about the vertical axis. This motion is called precession. For any point on the rotation axis of the top, the position vector is parallel to the angular momentum vector.
The weight of the top exerts an external torque about the origin (the coordinate system is defined such that the origin coincides with the contact point of the top on the floor, see Figure 12.12). The magnitude of this torque is
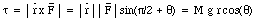
The direction of the torque is perpendicular to the position vector and to the force. This also implies that the torque is perpendicular to the angular momentum of the spinning top. The external torque causes a change in the angular momentum of the system
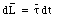
This equation shows that the change in the angular momentum dL that occurs in a time dt must point in the same direction as the torque vector. Since the torque is at right angle to L, it can not change the magnitude of L, but it can change its direction. The result is a rotation of the angular momentum vector around the z-axis. The precession angle d[phi] is related to the change in the angular momentum of the system:
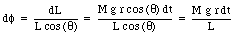
This shows that the precession velocity is equal to
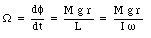
This equation shows that the faster the top spins the slower it precesses. In addition, the precession is zero if g = 0 m/s2 and the precession is independent of the angle [theta].