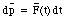
In a collision, strong mutual forces act between a few particles for a short time. These internal forces are significantly larger than any external forces during the time of the collision. The laws of conservation of linear momentum and energy, applied to the "before" and "after" situations, often allows us to predict the outcome of a collision. A great deal can be learned about the interactions between the colliding particles from the observed collision products.
Note:
Suppose a force F acts during a collision. The result of the collision force will be a change in the momentum of the particles involved. The amount of change depends not only on the average value of the force, but also on the time period during which it acts. The change in momentum dp is related to the collision force F as
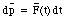
The total change in the of momentum during the collision is given by
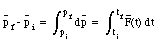
The right hand side of this equation is a measure of both the strength and the duration of the collision force. It is called the collision impulse J:
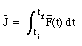
The unit of the impulse is N . s. From the definition of the impulse J we see that the relation between the impulse and the change of momentum is given by
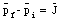
If the average collision force Fav acts during a time period equal to [Delta]t, the impulse J is equal to
Fav [Delta]t = J
Sample Problem 10-1
A baseball of mass m in horizontal flight with speed vi is struck by a batter. After leaving the bat, the ball travels in the opposite direction with a speed vf. What impulse J acts on the ball while it was in contact with the bat ?
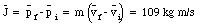
If the impact time is [Delta]t, what is the average force that acts on the baseball ?
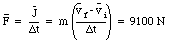
What is the average acceleration of the baseball during this period ?
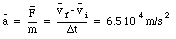
Consider the collision shown in Figure 10.1. If there are no external forces acting on this system (consisting of the two masses) the total momentum of the system is conserved. The first class of collisions we will discuss are the elastic collisions. Collisions are called elastic collisions if the total kinetic energy of the system is conserved. Applying conservation of linear momentum to the collision shown in Figure 10.1 gives
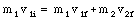
Conservation of the total kinetic energy gives
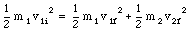
We now have two equations with two unknown (v1f and v2f) which can be solved. The first equation can be rewritten as
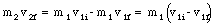
The second equation can be rewritten as
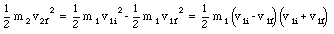
The final velocity of mass m1 can now be calculated by dividing the last two expressions
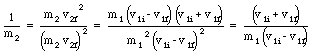
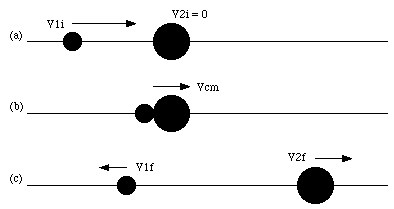
Figure 10.1. Collision in One-Dimension.
This gives
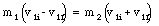
The final velocity of m1 can now be obtained
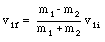
The final velocity of mass m2 can also be obtained
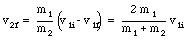
It is clear that the velocity of m2 is always positive. The velocity of m1 can be either positive or negative, depending on the masses of the two objects: v1f is negative if m2 > m1, and positive if m2 < m1.
In Chapter 9 we have shown that the motion of the center of mass is unaffected by the collision. The velocity of the center of masscenter of mass velocity can be calculated easily
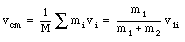
It can be easily verified that the velocity of the center of mass after the collision is the same as it was before the collision (as it should be of course since there are no external forces acting on the system).
Some Special Cases
The previously derived equations show that in this case
v1f = 0 m/s
v2f = v1i
In head-on collisions, particles of equal mass simply exchange velocities.
Using the previously derived expressions for v1f and v2f we obtain
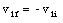
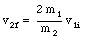
The projectile simply bounces back and the final velocity of the target will be a very small fraction of the initial velocity of the projectile.
Using the previously derived expressions for v1f and v2f we obtain
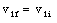
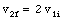
The velocity of the projectile is almost unchanged while the target will move with twice the initial velocity of the projectile.
The collision force acting between the target and the projectile is an internal force of the system under consideration consists of these two objects. The motion of the center of mass of a number of objects is solely determined by the external forces acting on the system (see Chapter 9).
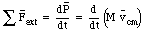
This equation shows that if no external forces act on the system, the velocity of its center of mass is constant.
Sample Problem 10-4
In a nuclear reactor, newly-produced fast neutrons must be slowed down before they can participate effectively in the chain-reaction process. By what fraction is the kinetic energy of a neutron (mass m1) reduced in a head-on collision with a nucleus of mass m2 (initially at rest) ?
Suppose v1i is the initial velocity of the neutron. Its final velocity, v1f, can be obtained using one of the previously derived equations:
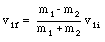
The initial kinetic energy of the neutron is given by
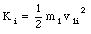
The final kinetic energy of the neutron is given by
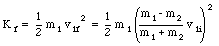
The fraction of the kinetic energy of the neutron lost in the collision is given by
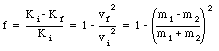
This is equal to
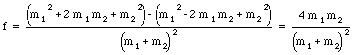
Since the mass units in the equation for f cancel, we can use atomic mass units:
mass Pb: 206 amu => f = 0.019 = 1.9 %
mass C: 12 amu => f = 0.28 = 28 %
mass H: 1 amu => f = 1.00 = 100 %
We conclude that any compound that contains large amounts of H will be a good moderator.
Example Problem 10-1
A glider whose mass is m2 rests on an air track. A second glider, whose mass is m1, approaches the target glider with a velocity v1i and collides elastically with it. The target glider rebounds elastically from the end of the track and meets the projectile glider a second time (see Figure 10.2). At what distance from the end of the air track will the second collision occur ?
The velocity of m1 and m2 after the first collision are given by
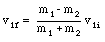
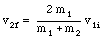
Suppose the second collision occurs a distance x from the end of the track (see Figure 10.2). At that point, mass m1 has traveled a distance (d - x) after the first collision and mass m2 has traveled a distance (d + x). Both masses must cover these distances of course in the same time
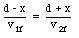
This can be rewritten as
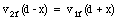
or
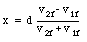
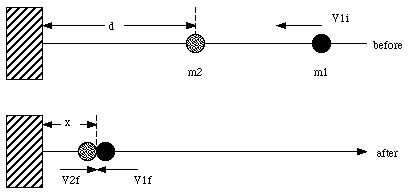
Figure 10.2. Example Problem 10-1.
Substituting the expressions for v1f and v2f in the expression for x, we obtain
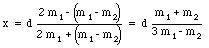
A special case occurs when m1 = m2. In this case, x = d. Note: v1f = 0 m/s and v2f = v1i.
If no external forces act on a system, its momentum is conserved. However, kinetic energy is not always conserved. An example of an inelastic collision is a collision in which the particles stick together (after the collisions). This type of a collision is a completely inelastic collision (of course, even in a completely inelastic collision, the total energy is conserved. The lost kinetic energy is converted into another form of energy: for example, thermal energy, energy of deformation etc.)
Example Problem 10-2
Suppose a mass m1 is moving with an initial velocity vi and collides with a mass m2, which is initially at rest (see Figure 10.3). The two masses stick together. What is the final velocity of the system, and what is the change in the kinetic energy of the system ?
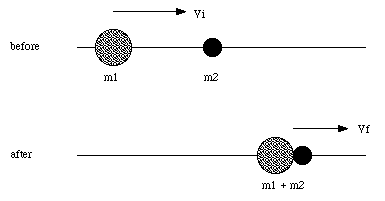
Figure 10.3. Completely Inelastic Collision.
The initial momentum of the system is
pi = m1 vi
The final momentum of the system is
pf = (m1 + m2) vf
Conservation of linear momentum implies
m1 vi = (m1 + m2) vf
or
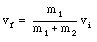
The final velocity of the combined system will always be less than that of the incoming object.
The initial kinetic energy of the system is
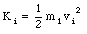
The final kinetic energy of the system is
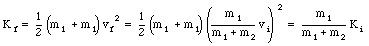
Note: not all the kinetic energy can be lost, even in a completely inelastic collision, since the motion of the center of mass must still be present. Only if our reference frame is chosen such that the center-of-mass velocity is zero, will the final kinetic energy in a completely inelastic collision be zero.
Sample Problem 10-5: The ballistic pendulum.
Suppose a bullet of mass m1 hits a large block of wood of mass m2. As a result, the block plus bullet swings upwards (maximum height is h). What is the velocity of the bullet ?
Suppose the velocity of the bullet is vi. The initial momentum of the system is
pi = m1 vi
The final velocity of the block plus bullet is vf. The final momentum is
pf = (m1 + m2) vf
Conservation of linear momentum implies
m1 . vi = (m1 + m2) vf
or
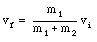
The initial kinetic energy of the block plus bullet is
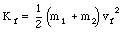
Since it is assumed that the block plus bullet swing frictionless, the total mechanical energy of the block plus bullet must be conserved. At its highest point, the mechanical energy of the block plus bullet is equal to
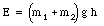
Conservation of mechanical energy implies that
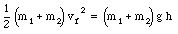
or
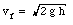
The velocity of the bullet can now be calculated
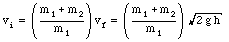
Suppose a mass m1, with initial velocity v1i, undergoes a collision with a mass m2 (which is initially at rest). The particles fly of at angles [theta]1 and [theta]2, as shown in Figure 10.4. Since no external forces act on the collision system, linear momentum is conserved (in both x and y direction):
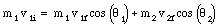
and
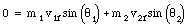
If the collision is elastic, kinetic energy also needs to be conserved:
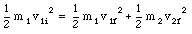
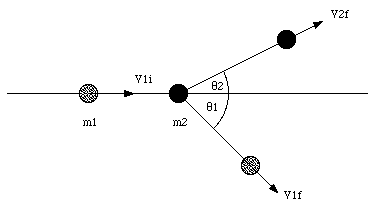
Figure 10.4. A Collision in Two Dimensions.
The variables are:
Example Problem 10-3
A beam of nuclei with mass m1 and velocity v1 is incident on a target nucleus with mass m2 which us initially at rest. The velocity and scattering angles of both reaction products is measured. Determine the masses of the reaction products and the change in kinetic energy.
The collision is schematically shown in Figure 10.5. Conservation of linear momentum along the x-axis requires
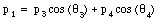
where p1, p3 and p4 are the momenta of particle 1, particle 3 and particle 4, respectively. Conservation of linear momentum along the y-axis requires
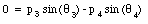
The last equation can be rewritten as
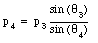
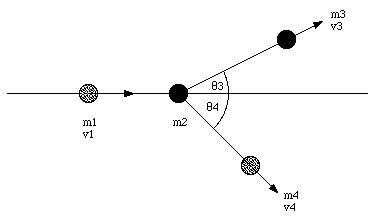
Figure 10.5. Example Problem 10-3.
Substituting this in the first equation we obtain
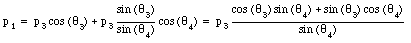
This immediately shows that
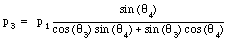
or
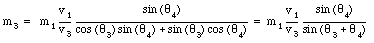
This relation can be used to find p4
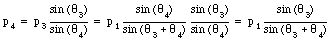
and m4
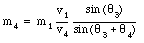
The change in the kinetic energy of the system can now be calculated
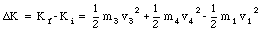
Example Problem 10-4
A 20 kg body is moving in the direction of the positive x-axis with a speed of 200 m/s when, owing to an internal explosion, it breaks into three parts. One part, whose mass is 10 kg, moves away from the point of explosion with a speed of 100 m/s along the positive y-axis. A second fragment, with a mass of 4 kg, moves along the negative x-axis with a speed of 500 m/s.
a). What is the speed of the third (6 kg) fragment ?
b) How much energy was released in the explosion (ignore gravity) ?
The problem is schematically illustrated in Figure 10.6. Since the force of the explosion is an internal force, the total momentum of the system will be conserved. We therefore can apply this conservation law both along the x-axis and along the y-axis. Conservation of linear momentum along the x-axis requires
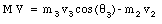
Conservation of linear momentum along the y-axis requires
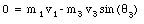
These equations can be rewritten as
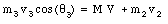
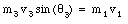
Squaring both equations and adding them gives
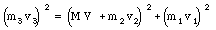
Solving this equation gives v3 = 1014 m/s. The energy supplied by the explosion is now easy to calculate:
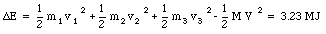
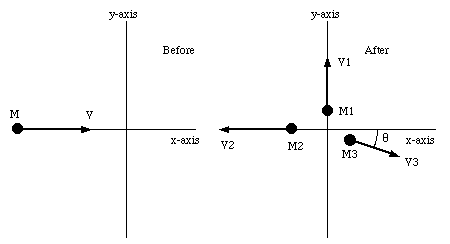
Figure 10.6. Example Problem 10-4.