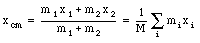
The motion of a rotating ax thrown between two jugglers looks rather complicated, and very different from the standard projectile motion discussed in Chapter 4. Experiments have shown that one point of the ax follows a trajectory described by the standard equations of motion of a projectile. This special point is called the center of mass of the ax.
The position of the center of mass of a system of two particles with mass m1 and m2, located at position x1 and x2, respectively, is defined as
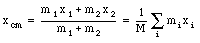
Since we are free to define our coordinate system in whatever way is convenient, we can define the origin of our coordinate system to coincide with the left most object (see Figure 9.1). The position of the center of mass is now
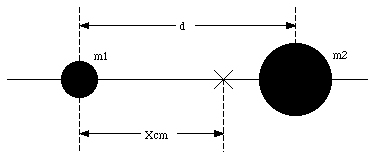
Figure 9.1. Position of the center of mass in 1 dimension.
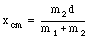
This equation shows that the center of mass lies between the two masses, closest to the heavier mass. In general, for a system with more than two particles, the position of the center of mass will satisfy the following relation
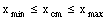
The definition of the center of mass in one dimension can be easily generalized to three dimensions
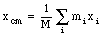
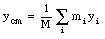
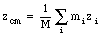
or in vector notation
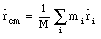
For a rigid body, the summation will be replaced by an integral
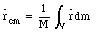
Suppose we are dealing with a number of objects. Figure 9.2 shows a system consisting of 4 masses, m1, m2, m3 and m4, located at x1, x2, x3 and x4, respectively. The position of the center of mass of m1 and m2 is given by
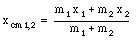
The position of the center of mass of m3 and m4 is given by
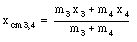
The position of the center of mass of the whole system is given by
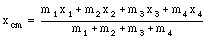
This can be rewritten as
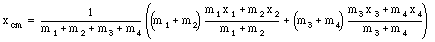
Using the center of mass of m1 and m2 and of m3 and m4 we can express the center of mass of the whole system as follows
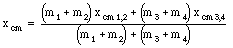

Figure 9.2. Location of 4 masses.
This shows that the center of mass of a system can be calculated from the position of the center of mass of all objects that make up the system. For example, the position of the center of mass of a system consisting out of several spheres can be calculated by assuming that the mass of each sphere is concentrated in the center of that sphere (its center of mass).
Note:
Sample Problem 9-3
Figure 9.3a shows a circular metal plate of radius 2R from which a disk if radius R has been removed. Let us call it object X. Locate the center of mass of object X.
Symmetry arguments immediately tell us that the center of mass of object X is located on the x-axis. Suppose the hole in object X is filled with a disk of radius R. The new object (object C, Figure 9.3b) is symmetric around the origin of our coordinate system, and that point is therefore the center of mass of object C. However, object C consist out of object X and a disk with radius R centered on the x-axis at x = - R (this disk is called object D). The center of mass of this system (consisting out of object X and object D) can be easily calculated:
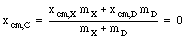
This equation can be rewritten as
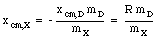
For a homogeneous disk (with density [rho]) the masses of object X and D can be calculated

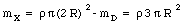
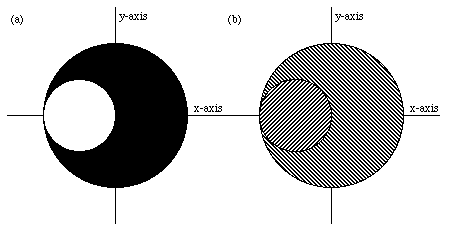
Figure 9.3. Sample Problem 9-3.
The position of the center of mass of object X is given by
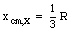
Example Problem 9-1
Figure 9.4 shows a one-dimensional rod. The density of the rod is position dependent : [rho](x) = a - bx + cx2. Determine the location of the center-of-mass of the rod.
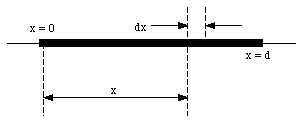
Figure 9.4. Position Dependent Density.
The mass of a fraction of the rod (length dx) is given by
dm = [rho](x) dx
The position of the center of mass of the rod can be determined as follows
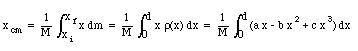
After evaluating the integral we obtain
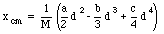
The total mass of the rod can be obtained easily
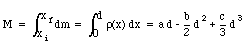
The definition of the center of mass of a system of particles can be rewritten as
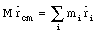
where M is the total mass of the system. Differentiating this equation with respect to time shows
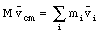
where vcm is the velocity of the center of mass and vi is the velocity of mass mi. The acceleration of the center of mass can be obtained by once again differentiating this expression with respect to time
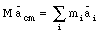
where acm is the acceleration of the center of mass and ai is the acceleration of mass mi. Using Newton's second law we can identify mi ai with the force acting on mass mi. This shows that
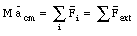
This equation shows that the motion of the center of mass is only determined by the external forces. Forces exerted by one part of the system on other parts of the system are called internal forces. According to Newton's third law, the sum of all internal forces cancel out (for each interaction there are two forces acting on two parts: they are equal in magnitude but pointing in an opposite direction and cancel if we take the vector sum of all internal forces). See Figure 9.5.
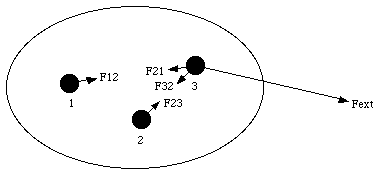
Figure 9.5. Internal and External Forces acting on a System of Particles.
The previous equations show that the center of mass of a system of particles acts like a particle of mass M, and reacts like a particle when the system is exposed to external forces. They also show that when the net external force acting on the system is zero, the velocity of the center of mass will be constant.
Example Problem 9-2
The center of mass of an exploding rocket will follow the trajectory of a projectile. although its individual pieces can follow a quit complex trajectory. The forces of the explosion are internal to the system, and the only external force acting on the system is the gravitational force.
Example Problem 9-3
A ball of mass m and radius R is placed inside a spherical shell of the same mass m and inner radius 2R (see Figure 9.6a). The ball is released and moves back and forth before coming to rest at the bottom of the shell (see Figure 9.6b). What is the displacement of the system ?
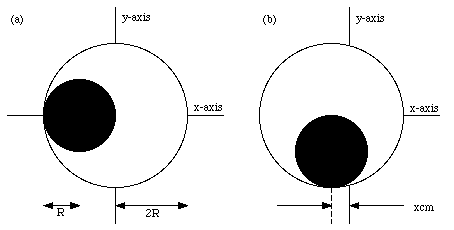
Figure 9.6. Example Problem 9-3.
The only external forces acting on the system are the gravitational force and the normal force. Both act in the y-direction. The x-component of the total external force acting on the system is zero. The x-component of the acceleration of the center of mass is therefore equal to zero. The velocity of the center of mass in the x-direction is initially equal to zero, and will therefore remain zero. We conclude that the position of the center of mass along the x-axis will not change. In the initial configuration (Figure 9.6a) the x-position of the center of mass is given by
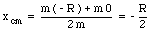
After the ball comes to rest, the x-coordinate of the center of mass of the system coincides with the x-coordinate of the center of the sphere (symmetry axis). Originally the center of the sphere was located at x = 0, and we conclude that the system is displaced over a distance R/2, to the left.
The linear momentum p of an object with mass m and velocity v is defined as
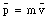
From this definition it is clear that the unit of momentum is (kg m/s) or (N s). Since this momentum is related to the linear motion of the object, it is called linear momentum. In Chapter 11 we will be discussing angular momentum which is the momentum related to the angular motion of the object.
Under certain circumstances the linear momentum of a system is conserved. The linear momentum of a particle is related to the net force acting on that object:

The rate of change of linear momentum of a particle is equal to the net force acting on the object, and is pointed in the direction of the force. If the net force acting on an object is zero, its linear momentum is constant (conservation of linear momentum).
The total linear momentum p of a system of particles is defined as the vector sum of the individual linear momenta
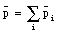
This expression can be rewritten as
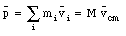
where M is the total mass of the system. We conclude that
" The linear momentum of a system of particles is equal to the product of the total mass M of the system and the velocity of the center of mass. "
If we differentiate linear momentum of the center-of-mass with respect to time we obtain

This expression shows that if the net external force acting on a system of particles is zero (Fext = 0 N), the linear momentum of the system is conserved.
Example Problem 9-4
A stream of bullets with mass m is fired horizontally with speed v into a large wooden block with mass M that is initially at rest on a horizontal table. If the block is free to slide across the table (without friction), what speed will it acquire after it has absorbed n bullets ?
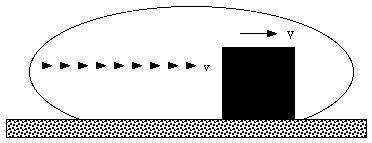
Figure 9.7. Example Problem 9-4.
Consider the closed system shown in Figure 9.7. This is an isolated system; no particles leave or enter the system. The rate of change of its linear momentum is therefore equal to the net external force. In this system, all external forces (normal and gravitational force) act in the y-direction, and we can conclude that the linear momentum in the x-direction is conserved. The system shown in Figure 9.7 consist initially out of n bullets, each moving with speed v, and the wooden block which is at rest. The total linear momentum in the x-direction is therefore
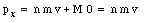
After the n bullets strike the wooden block, its mass is increased to (M + n m) and its velocity is V. The x-component of the linear momentum at that point is therefore
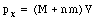
Since the linear momentum along the x-axis is conserved we conclude
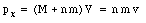
or

The final velocity V of the wooden block will always be less than the velocity of the bullets (independent of how many bullets we fire).
Note: we did not have to consider what happened when the bullets hit the block since these forces are internal forces.
Sample Problem 9-10
Two blocks with mass m1 and mass m2 are connected by a spring and are free to slide on a frictionless horizontal surface. The blocks are pulled apart and then released from rest. What fraction of the total kinetic energy will each block have at any later time ?
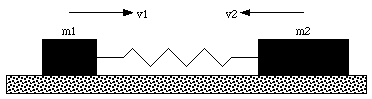
Figure 9.8. Sample Problem 9-10.
Figure 9.8 shows a schematic of the system. The velocities of mass m1 and mass m2 are defined to be positive when they are directed towards the right in Figure 9.8 (in Figure 9.8 the velocity of m2 is negative).
Consider the system consisting of the two masses and the spring. This is a closed system. The only external forces acting on the system are the gravitational force and the normal force. Both these forces are directed vertically. The net force along the x-axis is zero, and therefore, linear momentum is conserved along the x-axis.
Initially, both masses are at rest, and the total linear momentum along the x-axis is zero. Suppose at a later time mass m1 has a velocity equal to v1 and mass m2 has a velocity equal to v2. The total linear momentum at that time is then given by
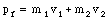
Since the linear momentum along the x-axis is conserved, pf must be equal to 0. The velocity v2 of mass m2 can now be expressed in terms of m1 and v1:
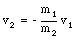
This shows that the velocity of mass m1 and of mass m2 always have opposite sign. The kinetic energy of mass m1 and mass m2 can now be calculated
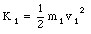
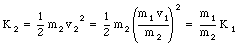
The total kinetic energy of the system is
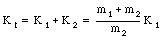
If f1 is the fraction of the total kinetic energy that is carried by mass m1 we obtain the following equation for f1:
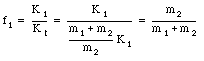
Problem 43P
A vessel at rest explodes, breaking into three pieces. Two pieces, having equal mass, fly off perpendicular to one another with the same speed of 30 m/s. The third piece has three times the mass of each of the other pieces. What is the direction and magnitude of its velocity immediately after the explosion ?
The vessel is an isolated system on which no external forces are acting. This implies that the total linear momentum of the system is conserved. Since the vessel is initially at rest, the initial linear momentum of the system is zero. Since the total linear momentum is conserved, the final linear momentum of the system must also be zero. Figure 9.9 shows schematically the direction of the three fragments in which the vessel explodes. The problem states that m1 = m2 and that m3 = 3 m1. Assuming that the total mass of the system is conserved we conclude that
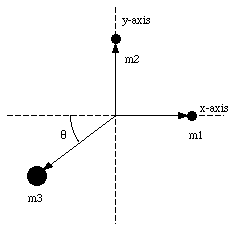
Figure 9.9. Problem 39P.
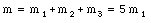
or
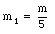
The problem also states that v1 = v2 = 30 m/s. Conservation of linear momentum along the x-axis and along the y-axis requires
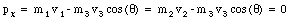
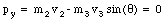
These two equations can be rewritten in the following manner
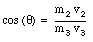
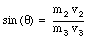
These two equation can be combined to give
tan ([theta]) = 1
or
[theta] = 45deg.
The velocity of the third fragment can now be obtained easily
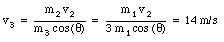
Problem 48P
A 1400 kg cannon, which fires a 70 kg shell with a muzzle speed of 556 m/s, is set at an elevation of 39deg. above the horizontal. The cannon is mounted on frictionless rails, so that it recoils freely. (a) What is the speed of the shell with respect to the earth ? (b) At what angle with the ground is the shell projected ?
The mass of the cannon is M, and the mass of the shell is m. The firing angle is [theta] and the muzzle speed is v0. The velocity of the cannon and the shell in with respect to the earth is vc and vs, respectively. The angle of projection of the shell with respect to the earth is a.
The external forces acting on the shell and cannon are the gravitational force and the normal force. These forces are directed along the y-axis. Since there is no external force acting on the shell along the x-axis, the linear momentum of the system along the x-axis is conserved. The total linear momentum of the system along the x-axis (the horizontal axis) is given by (see figure 9.10)
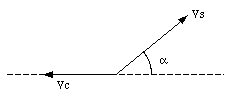
Figure 9.10. Velocity diagram of shell and canon.
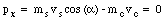
This implies that
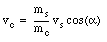
The muzzle speed provided in this problem is measured with respect to the muzzle. Since the cannon is not at rest, the speed of the shell with respect to the earth will be different than the speed of the shell with respect to the muzzle. The relation between these velocities and the firing angles is schematically shown in Figure 9.11. The figure clearly shows the following relations between the various velocities and firing angles:
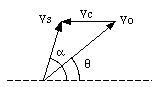
Figure 9.11. Velocity diagram of shell.
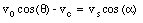
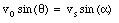
The first equation can be used to eliminate vc
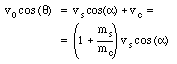
Using the last two equations, this expression can be rewritten as
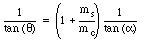
or
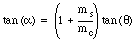
We conclude that a = 40.4deg.. The velocity of the shell with respect to the earth is given by
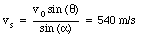
The motion of a rocket is a nice example of a system with a variable mass in which nevertheless conservation of linear momentum can be applied. Suppose a rocket is flying through deep space (no friction force and no gravitational force). It is burning fuel. Suppose at some time t the mass of the rocket is M. During a time interval [Delta]t, the mass of the rocket changes by [Delta]M:
M(t + [Delta]t) = M(t) + [Delta]M
Since the rocket is burning fuel, [Delta]M is negative. The mass of the exhaust products is - [Delta]M. The result of the burning of fuel is a change in the velocity of the rocket:
v(t + [Delta]t) = v(t) + [Delta]v
If we consider our system to consist of the rocket and the exhaust generated during the time interval [Delta]t, we are dealing with a closed system. Since there are no external forces acting on the system, the total linear momentum of the system is conserved. The initial linear momentum of the system (at time t) is given by
pi = M(t) v(t)
The final linear momentum of the system is given by
pf = (M(t) + [Delta]M) (v(t) + [Delta]v) + (- [Delta]M) U
where U is the velocity of the exhaust. Conservation of linear momentum therefore requires that
M(t) v(t) = (M(t) + [Delta]M) (v(t) + [Delta]v ) + (- [Delta]M) U
The exhaust velocity of the rocket depends on the design of the rocket engine. Suppose that for the engine used the velocity of the exhaust relative to the engine is measured to be U0. In the frame of reference in which the rocket is moving, the exhaust velocity is a function of both U0 and the velocity of the rocket
U - U0 = v(t) + [Delta]v
Using this expression we can rewrite the expression for conservation of linear momentum as follows
M(t) v(t) = (M(t) + [Delta]M) (v(t) + [Delta]v) + (- [Delta]M) (v(t) + [Delta]v + U0)
or
M(t) v(t) = M(t) (v(t) + [Delta]v) - [Delta]M U0
We conclude
[Delta]M U0 = M(t) [Delta]v
Dividing each side by [Delta]t gives
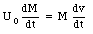
Now:
R u = M a
The mass used in the "first rocket equation" is of course time dependent (related to R). In order to find the velocity of the rocket (after burning some fuel) we return to the differential equation previously discussed
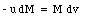
or
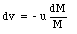
Integrating both sides gives
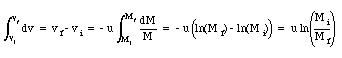
We conclude
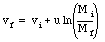
which is the "second rocket equation".