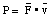
In this chapter we will introduce the concepts of work and kinetic energy. These tools will significantly simplify the manner in which certain problems can be solved.

Figure 7.1. A force F acting on a body. The resulting displacement is indicated by the vector d.
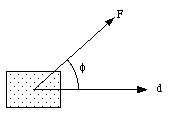
Suppose a constant force F acts on a body while the object moves over a distance d. Both the force F and the displacement d are vectors who are not necessarily pointing in the same direction (see Figure 7.1). The work done by the force F on the object as it undergoes a displacement d is defined as
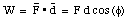
The work done by the force F is zero if:
* d = 0: displacement equal to zero
* [phi] = 90deg.: force perpendicular to displacement
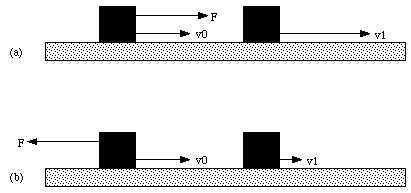
Figure 7.2. Positive or Negative Work.
The work done by the force F can be positive or negative, depending on [phi]. For example, suppose we have an object moving with constant velocity. At time t = 0 s, a force F is applied. If F is the only force acting on the body, the object will either increase or decrease its speed depending on whether or not the velocity v and the force F are pointing in the same direction (see Figure 7.2). If (F * v) > 0, the speed of the object will increase and the work done by the force on the object is positive. If (F * v) < 0, the speed of the object will decrease and the work done by the force on the object is negative. If (F * v) = 0 we are dealing with centripetal motion and the speed of the object remains constant. Note that for the friction force (F * v) < 0 (always) and the speed of the object is always reduced !
Per definition, work is a scalar. The unit of work is the Joule (J). From the definition of the work it is clear that:
1 J = 1 N m = 1 kg m2/s2
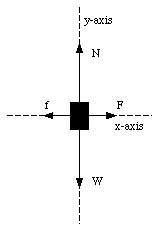
Figure 7.3. Forces acting on the safe.
Sample Problem 7-2
A safe with mass m is pushed across a tiled floor with constant velocity for a distance d. The coefficient of friction between the bottom of the safe and the floor is uk. Identify all the forces acting on the safe and calculate the work done by each of them. What is the total work done ?
Figure 7.3 shows all the forces that act on the safe. Since the safe is moving with constant velocity, its acceleration is zero, and the net force acting on it is zero
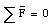
The components of the net force along the x-axis and along the y-axis must therefore also be zero
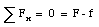
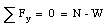
The second equation shows that N = W = m g. The force that is applied to the safe can now be calculated
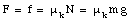
The work done on the safe by each of the four forces can now be calculated:
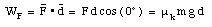
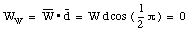
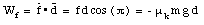
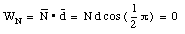
The total work done on the safe is therefore
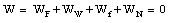
which could be expected since the net force on the safe is zero.
Example Problem 1
A crate with mass m is pulled up a slope (angle of inclination is [theta]) with constant velocity. Calculate the amount of work done by the force after the crate has moved to a height h (see Figure 7.4).
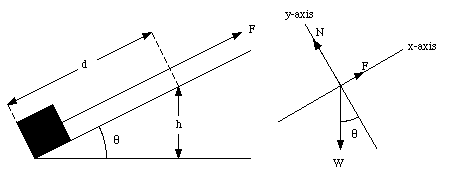
Figure 7.4. Example Problem 1.
The coordinate system that will be used is shown in Figure 4. Since the crate is moving with a constant velocity, the net force in the x and y direction must be zero. The net force in the x direction is given by
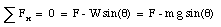
and the force F required to move the crate with constant velocity is hereby fixed:
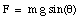
This force acts over a distance d. The value of d is fixed by the angle [theta] and the height h:
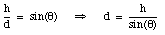
(see Figure 7.4). The work done by the force on the crate is given by
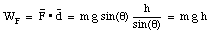
The work done on the crate by the gravitational force is given by
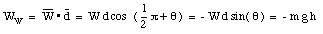
The work done on the crate by the normal force N is zero since N is perpendicular to d. We conclude that the total work done on the crate is given by
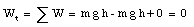
which was expected sine the net force on the crate is zero.
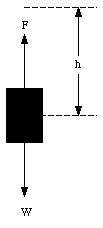
Figure 7.5. Crate moved in vertical direction.
If the same crate had been lifted by a height h in the vertical direction (see Figure 7.5), the force F required to produce a constant velocity would be equal to
F = m g
This force acts over a distance h, and the work done by this force on the object is
WF = m g h
which is equal to the work done by the force on the inclined slope. Although the work done by each force is the same, the strength of the required force is very different in each of the two cases.
Example Problem 2
A 3.57 kg block is drawn at constant speed 4.06 m along a horizontal floor by a rope exerting a 7.68 N force at angle of 15deg. above the horizontal. Compute (a) the work done by the rope on the block, and (b) the coefficient of kinetic friction between block and floor.
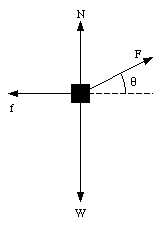
Figure 7.6. Example Problem 2.
A total of four forces act on the mass m: the gravitational force W, the normal force N, the friction force fk and the applied force F. These four forces are shown schematically in Figure 7.6. Since the velocity of the mass is constant, its acceleration is equal to zero. The x and y-components of the net force acting on the mass are given by
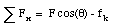
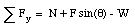
Since the net force acting on the mass must be zero, the last equation can be used to determine the normal force N:
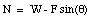
The kinetic friction force fk is given by
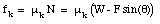
However, since the net component of the force along the x-axis must also be zero, the kinetic friction force fk is also related to the applies force in the following manner
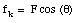
Combining these last two expressions we can determine the coefficient of kinetic friction:
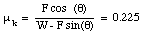
The work done by the rope on the mass m can be calculated rather easily:
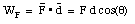
The work done by the friction force is given by
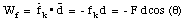
The work done by the normal force N and the weight W is zero since the force and displacement are perpendicular. The total work done on the mass is therefore given by
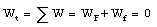
This is not unexpected since the net force acting on the mass is zero.
In the previous discussion we have assumed that the force acting on the object is constant (not dependent on position and/or time). However, in many cases this is not a correct assumption. By reducing the size of the displacement (for example by reducing the time interval) we can obtain an interval over which the force is almost constant. The work done over this small interval (dW) can be calculated
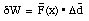
The total work done by the force F is the sum of all dW
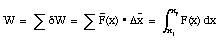
Example: The Spring
An example of a varying force is the force exerted by a spring that is stretched or compressed. Suppose we define our coordinate system such that its origin coincides with the end point of a spring in its relaxed state (see Figure 7.7). The spring is stretched if x > 0 and compressed if x < 0. The force exerted by the spring will attempt to return the spring to its relaxed state:
if x < 0: F > 0
if x > 0: F < 0
It is found experimentally that for many springs the force is proportional to x:
F = - k x
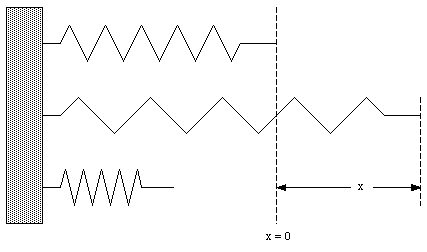
Figure 7.7. Relaxed, Stretched and Compressed Springs.
where k is the spring constant (which is positive and independent of x). The SI units for the spring constant is N/m. The larger the spring constant, the stiffer the spring. The work done by the spring on an object attached to its end can be calculated if we know the initial position xi and final position xf of the object:
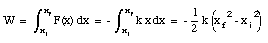
If the spring is initially in its relaxed state (xi = 0) we find that the work done by the spring is
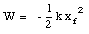
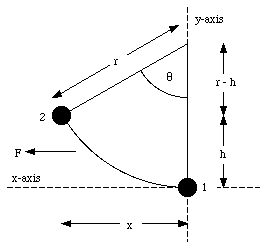
Figure 7.8. Pendulum in x-y plane
Consider the pendulum shown in Figure 7.8. The pendulum is moved from position 1 to position 2 by a constant force F, pointing in the horizontal direction (see Figure 7.8). The mass of the pendulum is m. What is the work done by the sum of the applied force and the gravitational force to move the pendulum from position 1 to position 2 ?
Method 1 - Difficult
The vector sum of the applied force and the gravitational force is shown in Figure 7.9. The angle between the applied force F and the vector sum Ft is a. Figure 7.9 shows that the following equations relate F to Ft and Fg to Ft:
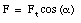
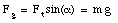
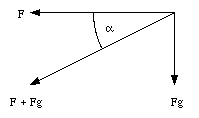
Figure 7.9. Vector sum Ft of Fg and F.
In order to calculate the work done by the total force on the pendulum, we need to know the angle between the total force and the direction of motion. Figure 7.10 shows that if the angle between the pendulum and the y-axis is [theta] , the angle between the total force and the direction of motion is [theta] + a. The distance dr is a function of d[theta]:
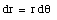
For a very small distance dr, the angle between dr and Ft will not change. The work done by Ft on the pendulum is given by
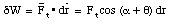
The total work done by Ft can be obtained by integrating the equation for dW over all angles between [theta] = 0deg. and [theta] = [theta]max. The maximum angle can be easily expressed in terms of r and h:
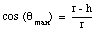
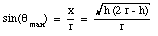
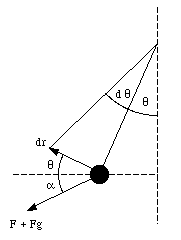
Figure 7.10. Angle between sum force and direction.
The total work done is
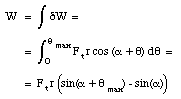
Using one of the trigonometric identities (Appendix, page A15) we can rewrite this expression as
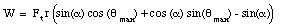
Using the equations shown above for Ft cos(a), Ft sin(a), r cos([theta]max) and r sin([theta]max) we can rewrite this expression and obtain for W:
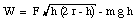
Method 2 - Easy
The total work done on the pendulum by the applied force F and the gravitational force Fg could have been obtained much easier if the following relation had been used:
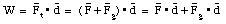
The total work W is the sum of the work done by the applied force F and the work done by the gravitational force Fg. These two quantities can be calculated easily:
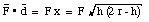
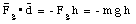
And the total work is
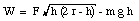
which is identical to the result obtained using method 1.
The observation that an object is moving with a certain velocity indicates that at some time in the past work must have been done on it. Suppose our object has mass m and is moving with velocity v. Its current velocity is the result of a force F. For a given force F we can obtain the acceleration of our object:
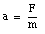
Assuming that the object was at rest at time t = 0 we can obtain the velocity at any later time:
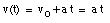
Therefore the time at which the mass reaches a velocity v can be calculated:
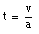
If at that time the force is turned off, the mass will keep moving with a constant velocity equal to v. In order to calculate the work done by the force F on the mass, we need to know the total distance over which this force acted. This distance d can be found easily from the equations of motion:
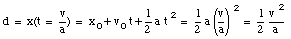
The work done by the force F on the mass is given by
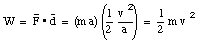
The work is independent of the strength of the force F and depends only on the mass of the object and its velocity. Since this work is related to the motion of the object, it is called its kinetic energy K:
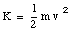
If the kinetic energy of a particle changes from some initial value Ki to some final value Kf the amount of work done on the particle is given by
W = Kf - Ki
This indicates that the change in the kinetic energy of a particle is equal to the total work done on that particle by all the forces that act on it.
Alternative Derivation
Consider a particle with mass m moving along the x-axis and acted on by a net force F(x) that points along the x-axis. The work done by the force F on the mass m as the particle moves from its initial position xi to its final position xf is
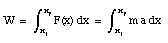
From the definition of a we can conclude
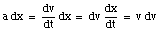
Substituting this expression into the integral we obtain
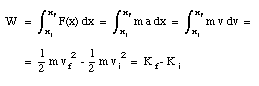
Example Problem 3
An object with mass m is at rest at time t = 0. It falls under the influence of gravity through a distance h (see Figure 7.11). What is its velocity at that point ?
Since the object is initially at rest, its initial kinetic energy is zero:
Ki = 0 J
The force acting on the object is the gravitational force
Fg = m g
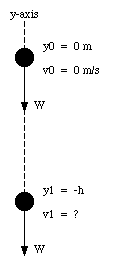
Figure 7.11. Falling Object.
The work done by the gravitational force on the object is simply
W = Fg h = m g h
The kinetic energy of the object after falling a distance h can be calculated:
W = m . g . h = Kf - Ki = Kf
and its velocity at that point is
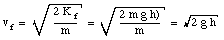
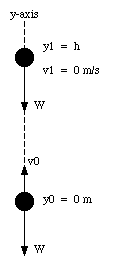
Figure 7.12. Projectile motion.
Example Problem 4
A baseball is thrown up in the air with an initial velocity v0 (see Figure 7.12). What is the highest point it reaches ?
The initial kinetic energy of the baseball is
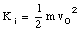
At its highest point the velocity of the baseball is zero, and therefore its kinetic energy is equal to zero. The work done on the baseball by the gravitational force can be obtained:
W = Kf - Ki = - Ki
In this case the direction of the displacement of the ball is opposite to the direction of the gravitational force. Suppose the baseball reaches a height h. At that point the work done on the baseball is
W = - m g h
The maximum height h can now be calculated:
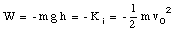
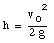
In every day life, the amount of work an apparatus can do is not always important. In general it is more important to know the time within which a certain amount of work can be done. For example: the explosive effect of dynamite is based on its capability to release large amounts of energy in a very short time. The same amount of work could have been done using a small space heater (and having it run for a long time) but the space heater would cause no explosion. The quantity of interest is power. The power tells us something about the rate of doing work. If an amount of work W is carried out in a time interval [Delta]t, the average power for this time-interval is
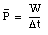
The instantaneous power can be written as
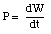
The SI unit of power is J/s or W (Watt). For example, our usage of electricity is always expressed in units of kilowatt . hour. This is equivalent to
7.3.1. kW . h = (103 W) (3600 s) = 3.6 x 106 J = 3.6 MJ
We can also express the power delivered to a body in terms of the force that acts on the body and its velocity. Thus for a particle moving in one dimension we obtain
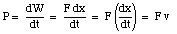
In the more general case of motion in 3 dimensions the power P can be expressed as