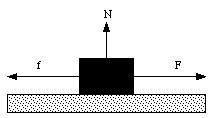

Figure 6.1. Static Friction.
Suppose that a horizontal force F is applied to a block resting on a rough surface (see Figure 6.1). As long as the applied force F is less than a certain maximum force (Fmax), the block will not move. This means that the net force on the block in the horizontal direction is zero. Therefore, besides the applied force F, there must be a second force f acting on the block. The force f must have a strength equal to F, and it must be pointing in the opposite direction. This force f is called the friction force, and because the block does not move, we are dealing with static friction. Experiments have shown that the force of static friction is largely independent of the area of contact and proportional to the normal force N acting between the block and the surface. The static friction force is
f <= us N
where us is the coefficient of static friction (which is dimensionless). The coefficient of static friction is approximately constant (independent of N). The maximum force that can be applied without moving the block is
Fmax = us N
Once the block has been set in motion, the force F needed to keep it in motion with a constant velocity is usually less than the critical force needed to get the motion started. In this situation we are dealing with kinetic friction and the friction force fk is given by
fk = uk N
where uk is the coefficient of kinetic friction. The kinetic friction force is independent of the applied force, but always points in the opposite direction. The equation for fk is not a vector equation since fk and N do not point in the same direction.
Note: The friction between car tires and the road is static friction. This friction is crucial when you try to stop a car. Since the maximum static friction force is larger than the kinetic friction force, a car can be stopped fastest if we prevent the wheels from locking up. When the wheels lock up, the friction force is changed to kinetic friction (the tires and the ground are moving with respect to each other) thereby reducing the acceleration and increasing the time and length required to bring the car to a halt.
Sample Problem 6-1
Figure 6.2 shows a mass m on an inclined slope. At a certain angle [theta] the mass begins to slide down the slope. Calculate the coefficient of static friction.
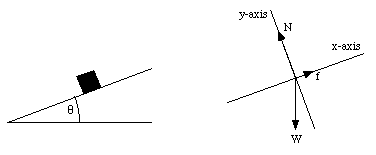
Figure 6.2. Coordinate System used in Sample Problem 1.
Figure 2 shows the coordinate system used in this problem. Note that with this choice of coordinate system, the normal force N and the friction force f have each only one component; N is directed along the y-axis and f is directed along the x-axis. Since this is the maximum angle at which the object will remain at rest, the friction force has reached it maximum value:
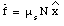
Since the object is at rest, the net force on the object equals zero:
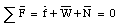
In terms of the components of the net force along the x-axis and the y-axis:
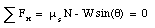
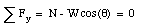
The coefficient of static friction can be easily obtained from these two equations:
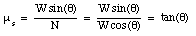
Note The friction force between car tires and the road is reduced when the car travels uphill or downhill. It is harder to drive uphill or downhill when the roads are slick than it is to drive on leveled surface.
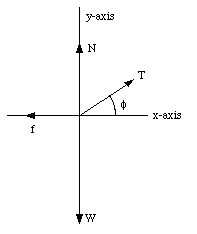
Figure 6.3. Free-Body Diagram for Sled.
Sample Problem 6-3
A woman pulls a loaded sled (mass m) along a horizontal surface at constant speed. The coefficient of kinetic friction between the runners and the snow is uk and the angle between the rope and the horizontal axis is [phi] (see Figure 6.3). What is the tension in the rope ?
Since the sled is moving with a constant velocity, the net force on the sled must be zero. Decomposing the net force into its components along the x-axis and the y-axis, we obtain the following equations of force:
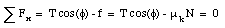

The second equation can be used to eliminate N:
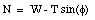
Substituting this expression in the first equation we obtain:
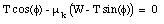
The tension T can now be calculated:
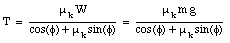
The normal force N is always perpendicular to the surface. In the previous two sample problems, the normal force N was proportional to the weight of the object. However, this is not always true. For example, suppose I am pressing an eraser against the blackboard. I ask myself, what is the minimum force that I need to apply in order to prevent the eraser from slipping ? This situation is shown schematically in Figure 6.4. Since the eraser is at rest, the net force acting on it must be zero (and therefore, the components of the net force in both the x and the y-direction must be equal to zero):
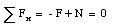
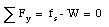
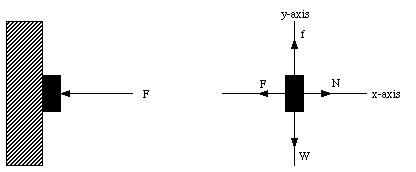
Figure 6.4. Eraser on the Black Board.
The second equation tells us that the static friction force fs must be equal to W. This implies the following for the normal force N:
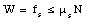
However, the normal force N is equal to the applied force F. In order to prevent the eraser from slipping, the force F will need to exceed a minimum threshold:
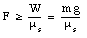
This relation shows that if the mass of the eraser is increased, the applied force needed to prevent the eraser from slipping will increase (the minimum force is proportional to the mass). This example also illustrates a situation in which the normal force is not related to the mass of the object.
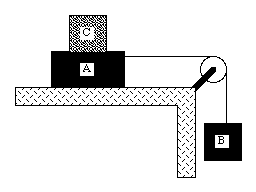
Figure 6.5. Problem 25P.
Problem 25P
In Figure 6.5, A, and B are blocks with weights of 44 N and 22N, respectively. (a) Determine the minimum weight of block C that must be placed on A to keep it from sliding if us between A and the table is 0.20. (b) Block C is suddenly lifted off A. What is the acceleration of block A, if uk between A and the table is 0.15 ?
A weight (block C) is placed on top of block A and prevents it from sliding. The acceleration of the system is therefore 0 m/s2. Consequently, the net force on each block is equal to 0 N. In order to determine the minimum weight of block C required to accomplish this, we start evaluating the net force on each block. The forces acting on block B, the weight WB and the tension T, are schematically indicated in Figure 6.6. The net force acting on block B is directed along the y-axis and has a magnitude equal to
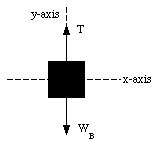
Figure 6.6. Forces acting on block B.
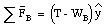
Since the net force acting on block B must be zero we conclude that
T = WB
The forces acting on block A and block C are indicated in Figure 6.7. The net force acting in the y-direction is zero and thus
N = WA + WC
Since the system remains at rest, the net force acting on block A and C along the x-direction must also be zero. This means that the static friction force fs must be equal to the tension T. Experiments show that fs has a maximum value which is determined by the normal force N and the static friction coefficient us
fs <= us N = us (WA + WC)
The minimum weight of block C that will prevent the system from slipping can be found by requiring that
us (WA + WC) >= fs = T = WB
and thus
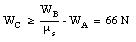
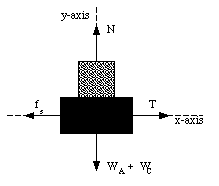
Figure 6.7. Forces acting on block A and C.
When block C is removed the static friction force is changed (since the normal force is changed). The maximum static friction force is now us WA = 8.8 N which is less than the weight of block B. Obviously block A will slip and both blocks will accelerate. At this point the friction force acting on block A is the kinetic friction force fk whose magnitude is equal to
fk = uk N = uk WA
The net force acting on block A is given by
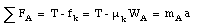
The net force acting on block B is given by
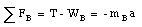
Eliminating the tension T from these last two equations we obtain for the acceleration a
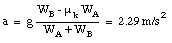
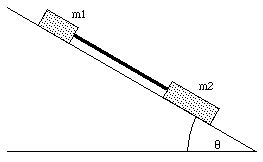
Figure 6.8. Problem 36P.
Problem 36P
Two masses, m1 = 1.65 kg and m2 = 3.30 kg, attached by a massless rod parallel to the inclined plane on which they both slide (see Figure 6.8), travel along the plane with m1 trailing m2. The angle of incline is 30deg.. The coefficient of kinetic friction between m1 and the incline is u1 = 0.226; that between m2 and the incline is u2 = 0.113. Compute (a) the tension in the rod and (b) the common acceleration of the two masses. (c) How would the answers to (a) and (b) change if m2 trailed m1 ?
The forces acting on mass m1 are schematically shown in Figure 6.9. The x and y-components of the net force acting on m1 are given by
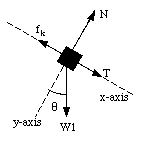
Figure 6.9. Forces acting on m1.
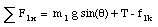
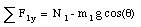
In the coordinate system chosen, there is no acceleration along the y-axis. The normal force N1 must therefore be equal to m1 g cos([theta]). This fixes the kinetic friction force
f1k = u1k N1 = u1k m1 g cos([theta])
Mass m1 will accelerate down hill with an acceleration a. The acceleration a is related to the x-component of the net force acting on mass m1
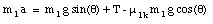
The forces acting on mass m2 are schematically shown in Figure 6.10. The friction force f2k acting on mass m2 can be determined easily (see calculation of f1k):
f2k = u2k N2 = u2k m2 g cos([theta])
The x-component of the net force acting on mass m2 is given by
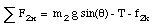
and is related to the acceleration a of mass m2
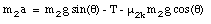
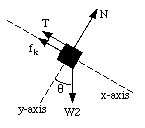
Figure 6.10. Forces acting on m2.
We now have two equations with two unknown (a and T). Eliminating the tension T from these two equations we obtain the following expression for a
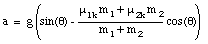
Substituting the values of the parameters given we find that a = 3.62 m/s2. The tension T in the rod can now be determined easily
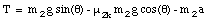
which is equal to 1.06 N. If mass m1 and mass m2 are reversed, we will still obtain the same acceleration, but the tension in the rod will be negative (which means that the rod is being compressed).
The friction force we have discussed so far acts when two surfaces touch. The force that tends to reduce the velocity of objects moving through air is very similar to the friction force; this force is called the drag force. The drag force D acting on an object moving through air is given by
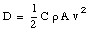
where A is the effective cross-sectional area of the body, [rho] is the density of air and v is the speed of the object. C is a dimensionless drag coefficient that depends on the shape of the object and whose value generally lies in the range between 0.5 and 1.0. The direction of the drag force is opposite to the direction of the velocity.
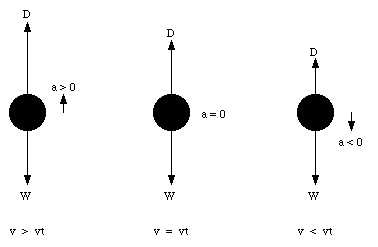
Figure 6.11. Drag Force.
Because of the drag force, a falling body will eventually fall with a constant velocity, the so called terminal velocity vt. When the object is moving with its terminal velocity vt the net force on it must be zero (no change in velocity means no acceleration). This occurs when D = mg, and the terminal velocity vt has to satisfy the following relation:
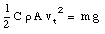
and vt is calculated to be
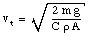
The equation for vt shows that the terminal velocity of an object increases with a decreasing effective area.
The terminal velocity of an object is the final velocity it obtains during free fall. The object will obtain this velocity independent of whether its initial velocity is larger or smaller than the terminal velocity (see Figure 6.11).
In chapter 4 we have seen that when a particle moves in a circle, it experiences an acceleration a, directed towards the center of the circle, with a magnitude equal to
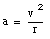
where v is the velocity of the particle, and r is the radius of the circle. The acceleration a is called the centripetal acceleration. To account for the centripetal acceleration, a centripetal force must be acting on this object. This force must be directed towards the center of the circle, and can be calculated from Newton's second law:
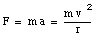
An example of uniform circular motion is the motion of the moon around the earth. Suppose the period of this motion is T. What does this tell us about the distance r between the earth and the moon ? During one period, the moon covers a total distance equal to 2[pi]r. The velocity of the moon, vm, can be calculated:
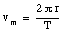
The corresponding centripetal force is
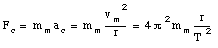
Here we assumed that mm is the mass of the moon. The centripetal force is supplied by the gravitational attraction between the earth and the moon. In Chapter 15 we will see that the strength of the gravitational interaction can be calculated as follows:
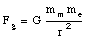
where G is the gravitational constant and me is the mass of the earth. For a constant circular motion, the gravitational force must provide the required centripetal force:
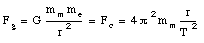
The distance between the earth and the moon can therefore be calculated:
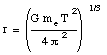
The constant of gravity is known to be G = 6.67 x 10-11 m3/(s kg) and the mass of the earth is known to be me = 5.98 x 1024 kg. The measured period of the moon is 27.3 days (2.3 x 106 s). The distance between the moon and the earth can therefore be calculated:
r = 3.82 x 108 m
which agrees nicely with the distance obtained using other techniques (for example the measurement of the time it takes for light to travel from the earth to the moon and back).
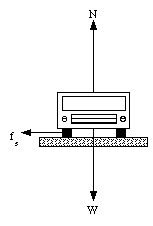
Figure 6.12. Forces acting on a car while rounding an unbanked curve.
Friction is critical if we want to round a curve while driving a car or bicycle. This can be easily understood if we consider the forces that act on a car while it is making a turn. Suppose that the car in question make a turn with radius R and velocity v. Figure 6.12 shows the forces acting on the car. There is no motion in the vertical direction and the net force in this direction must therefore be equal to zero. This requires that the normal force N is equal to the weight of the car:
N = m g
When the car rounds the curve it carries out uniform circular motion. The corresponding centripetal acceleration of this motion is given by
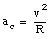
In order for the car to carry out this circular motion there must exist a radial force with a strength equal to
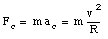
This force can only be supplied by the static friction force and therefore we require that
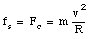
The static friction force fs has a maximum value equal to us N and this limits the velocity and the radius of curvature of the curve that the car can take:
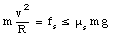
We conclude that the car will be able to make a turn with radius R and velocity v if the coefficient of static friction between the tires and the road is
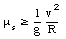
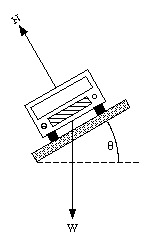
Figure 6.13. Forces acting on a car while rounding an banked curve.
If the road is frictionless (us = 0) because of a cover of ice, the car will not be able to round any curve at all. In order to avoid problems like this, curves on highways are usually banked. The effect of banking the curves can be easily understood. Figure 6.13 shows the forces acting on an automobile when it is rounding a curve on a banked highway. We assume that there is no friction between the tires and the road. The normal force N has components both along the radial and the vertical axes. Since there is no motion along the vertical direction, the net force along the vertical axis must be zero. This requires that
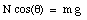
and fixes the normal force N
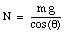
The radial component of the normal force is given by
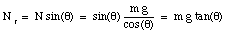
This component of the normal force can produce the radial acceleration required to allow the car to round the curve, even in the absence of friction. If the car has to round a curve with radius R and with velocity v, we require that
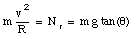
or
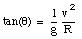
This last equation shows that the banking angle of a highway curve is designed for a specific velocity and radius of curvature.
Sample Problem 6-9
A conical pendulum whirls around in a horizontal circle at constant speed v at the end of a cord whose length is L. The cord makes an angle [theta] with the vertical. What is the period of the pendulum ?
The pendulum is shown schematically in figure 6.14. Since the pendulum is carrying out a uniform circular motion, the acceleration of the pendulum has to point toward the center of the circle (direction along the position vector r) and the magnitude of the acceleration equals v2/r, where v is the velocity of the pendulum and r is the radius of the circle. The net force in the horizontal plane should therefore be always directed towards the center of the circle and have strength determined by Newton's second law.
The coordinate system chosen is such that the origin coincides with the center of the circle describing the motion of the pendulum. Since the horizontal component of the force is always directed towards the center we will be using an r-axis (rather than an x-axis). The y-axis coincides with the vertical direction (see Figure 6.14). Since the y-coordinate of the bob is constant, the acceleration in y-direction must be zero. The net force in this direction must therefore be zero:
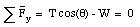
This expression allows us to calculate the tension T:
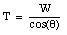
The net force in the radial direction can now be determined:
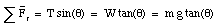
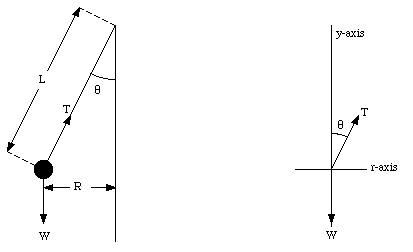
Figure 6.14. Sample Problem 6-9.
The centripetal acceleration a can now be calculated:
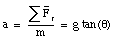
From the radius R of the trajectory and the centripetal acceleration a, the velocity of the object can be calculated:
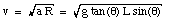
The period T can be calculated from the known velocity v and radius R:
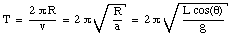
For L = 1.7 m and [theta] = 37deg. the period T = 2.3 s.
Sample Problem 6-10
A Cadillac with mass m moves at a constant speed v on a curved (unbanked) roadway whose radius of curvature is R. What is the minimum coefficient of static friction us between the tires and the roadway ?
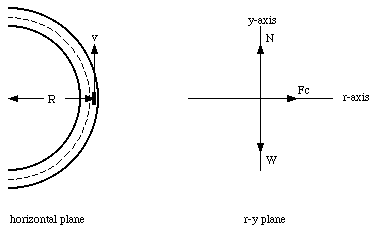
Figure 6.15. Sample Problem 6-10.
The situation is schematically shown in Figure 6.15. Since there is no acceleration in the y-direction, the net force in this direction must be zero:
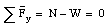
The centripetal force Fc is given by:
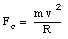
In this situation, the centripetal force is provided by the static friction force. If no slipping occurs, the maximum static friction force must exceed the required centripetal force:
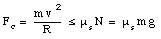
The minimum coefficient of static friction can be obtained from this equation:
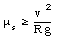
If the velocity of the car is 72 km/hr (20 m/s) and the radius of curvature R = 190 m, the minimum value of the coefficient of static friction is 0.21. Note that the mass of the car does not enter in the calculation, and the friction coefficient is therefore the same for all objects moving with the same velocity. The minimum coefficient of static friction scales with the square of the velocity; a reduction of the velocity by a factor if two, will reduce the minimum friction coefficient by a factor of four.
Problem 58E
A stunt man drives a car over the top of a hill, the cross section of which can be approximated by a circle of radius 250 m. What is the greatest speed at which he can drive without the car leaving the road at the top of the hill ?
The car will not leave the road at the top of the hill if the net radial force acting on it can supply the required centripetal acceleration. The only radial forces acting on the car are the gravitational force and the normal force (see Figure 6.16). The net radial force Fr acting on the car is equal to
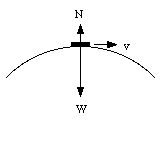
Figure 6.16. Forces acting on the car.
Fr = W - N
Since the normal force N is always directed along the positive y-axis, the radial force will never exceed the weight W of the car. This therefore also limits the centripetal force and therefore the speed of the car.
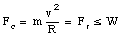
The maximum velocity of the car can now be found easily
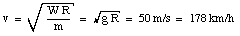
Suppose the car is driving with a velocity less than 178 km/h. The normal force N can now be calculated and will be a function of the velocity v. If the car carries out a uniform circular motion than we know that a net radial force must be acting on it and that its magnitude is equal to mv2/R. The net radial force acting on the car is equal to W - N. We conclude that
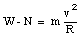
or
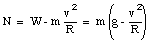
Problem 60P
A small object is placed 10 cm from the center of a phonograph turntable. It is observed to remain on the table when it rotates at 33 1/3 revolutions per minute but slides off when it rotates at 45 revolutions per minute. Between what limits must the coefficient of static friction between the object and the surface of the turntable lie ?
The object is located a distance R away from the rotation axis. During one revolution the object covers a distance 2[pi]R. If one revolution is completed during a time T, the linear velocity of the object can be obtained using the following equation:
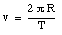
In order for the object to carry out such a uniform circular motion it must provide a radial force with magnitude equal to
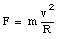
The only radial force acting on the object is the static friction force. The friction force fs has a maximum value given by
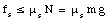
If the object remains on the table, the static friction coefficient needs to satisfy the following relation:
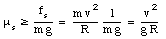
In this problem the distance to the rotation axis is 0.1 m. The block remains on the table when the table rotates at 33 1/3 rev/min. This corresponds to 1 revolution per 1.80 s, and a linear velocity of 0.35 m/s. This implies that the coefficient of static friction must be at least 0.12. When the table rotates at 45 rev/min the block leaves the table. This implies the coefficient of static friction is less than 0.22