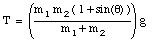
When an object all of a sudden changes its velocity and/or direction, we can always find an interaction between that object and its surroundings that is responsible for this change. We state that the surroundings exert a force on the object studied. Under the influence of a force, an object will accelerate. The force laws allow us to calculate the force acting on a body from the properties of the body and its environment. The laws of motion are subsequently used to calculate the acceleration of the object under influence of the force.
In this course we will be discussing the laws of motion obtained by Newton. This is called Newtonian mechanics. It should be realized that Newtonian mechanics does not always provide correct answers. If the speed of the objects involved is an appreciable fraction of the speed of light, we must replace Newtonian mechanics by Einstein's special theory of relativity. For problems on the scale of atomic structure we must replace Newtonian mechanics by quantum mechanics.
All around us we observe that all moving objects will come eventually to rest, unless we apply a force to them. We need to keep pedaling if we want to keep a bicycle going with constant speed, we need to have our engine running if we want to keep driving with a speed of 55 miles/hour. In all these cases, friction will ultimately stop any moving object, unless the friction force is canceled by the force supplied by our legs, our engine, etc. If we reduce friction, the moving object will take longer to slow down, and the force needed to overcome the friction force will be less. In the limit of no friction, our object will keep moving with a constant velocity, and no force need to be applied. This conclusion is summarized in Newton's first law:
" Consider a body on which no net force acts. If the body is at rest, it will remain at rest. If the body is moving with constant velocity, it will continue to do so. "
Newton's first law is really a statement about reference frames in that it defines the kinds of reference frames in which the laws of Newtonian mechanics hold. Reference frames in which Newton's first law applies are called inertial reference frames.
One way to test whether a reference frame is an inertial reference frame, is to put a test body at rest and arrange things so that no net force acts in it. If the reference frame is an inertial frame, the body will remain at rest; if the body does not remain at rest, the reference frame is not an inertial frame. If you put a bowling ball at rest on a merry-go-round, no identifiable forces act on the ball, but it does not remain at rest. Rotating reference frames are not inertial reference frames. Strictly speaking, the earth is therefore also not an inertial frame, however, only if we consider large scale motion such as wind and ocean current do we need to take into account the non inertial character of the rotating earth.
If we exert the same force on several objects with different mass, we will observe different accelerations. For example, one can throw a baseball significantly further (and faster) than a ball of similar size made of lead. The unit of force is the Newton (N), and a force of 1 N is defined as the force that when applied to an object with a mass of 1 kg, produces an acceleration of 1 m/s2. If we apply a force equal to 2 N, the corresponding acceleration is 2 m/s2.
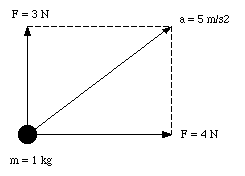
Experiments have shown that the force is a vector. This can be shown by demonstrating that the force has a magnitude and a direction. Suppose, we apply a force of 3 N to our standard object (mass 1 kg). The force is applied such that the resulting acceleration of 3 m/s2 is upwards (positive y-direction). In addition, we apply a force of 4 N in the horizontal direction (this force is applied such that the standard object will accelerate with an acceleration of 4 m/s2 in the direction of the positive x-axis if this is the only force applied). The situation is illustrated in Figure 5.1. If both forces are acting on the standard mass simultaneously, the acceleration of the object is measured to be 5 m/s2, and the direction of the acceleration coincides with the direction of the vector sum of the two forces. The total force is 5 N and is equal to the magnitude of the sum vector of the two forces (if we assume that the direction of the force is equal to the direction of the acceleration). We conclude that indeed the force is a vector and that both the force and the corresponding acceleration have the same direction.

Figure 5.1. The Acceleration of the standard body under the influence of two forces.
The acceleration produced by a certain force depends on the mass of the object. The acceleration of an object with twice the mass of the standard mass under the influence of a certain force is half that of the acceleration of the standard mass due to the same force. The following list summarizes what we have learned so far about forces:
1. Force is a vector.
2. A force acting on an object produces an acceleration. The direction of the acceleration is the same as the direction of the force applied.
3. For a given force, the resulting acceleration of a body with a mass twice that of the standard mass, is half that of the acceleration of the standard mass under the influence of the same force.
The conclusions are summarized in Newton's second law:'
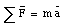
where [Sigma]F is the vector sum of all forces acting on an object with
mass m, and
 is the resulting acceleration (note: the sum includes only external forces).
If we decompose both the force and the acceleration into their individual
components along the x, y and z-axis, we obtain the following relations:
is the resulting acceleration (note: the sum includes only external forces).
If we decompose both the force and the acceleration into their individual
components along the x, y and z-axis, we obtain the following relations:
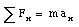
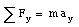
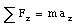
Newton's second law includes a formal statement of Newton's first law: if there is no net force acting on an object ([Sigma]F = 0 N) the acceleration is zero (and the velocity of the object is constant).
Sample Problem 5-1
A student pushes a loaded sled whose mass is 240 kg for a distance of 2.3 m over the frictionless surface of a frozen lake. He exerts a horizontal force equal to 130 N. If the sled starts from rest, what is its final velocity ?
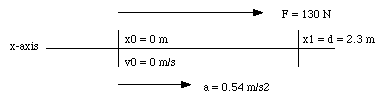
Figure 5.2. Coordinate System Sample Problem 5-1.
This is a one-dimensional problem. The coordinate system is defined such that the origin coincides with the position of the sled at time t = 0 s, and the force is applied in the positive direction (see Figure 5.2). Since the force is constant, the resulting acceleration a is also constant, and can be calculated by applying Newton's second law:
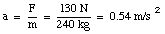
The constant acceleration is only applied over a distance d (= 2.3 m). In the coordinate system chosen, the equation of motion can be written as follows:
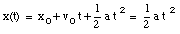
From this equation, the time at which the sled has covered a distance d can be calculated:
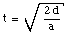
and the velocity of the sled at that time is equal to
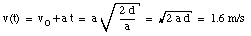
Sample Problem 5-2
In a two dimensional tug war, Alex, Betty and Charles pull on ropes that are tied to an automobile tire. The ropes make angles as shown in Figure 5.3, which is a view from above. Alex pulls with a force FA = 220 N and Charles with a force FC = 170 N. With what force must Betty pull in order to keep the tire stationary ?
Since the tire is stationary, the net force on the tire must be zero. This also means that the net force along the x and y direction must be zero:
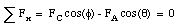
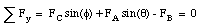
Substituting the known values for FA, FC and [theta] in the first equation, we can calculate [phi]:
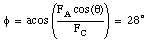
Substituting this value for [phi] into the second equation we can calculate FB:
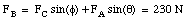
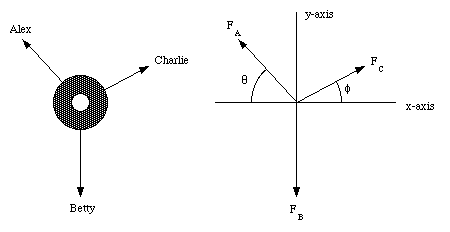
Figure 5.3. Force Diagram Sample Problem 5-2.
If a hammer exerts a force on a nail, the nail exerts an equal but oppositely directed force on the hammer. This is true in general, and is described by Newton's third law:'
" Suppose a body A exerts a force (FBA) on body B. Experiments show that in that case body B exerts a force (FAB) on body A. These two forces are equal in magnitude and oppositely directed:
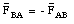
"
Note: Since the two members of an action-reaction pair always act on different bodies, they can not cancel each other.
The mass of a body and the weight of a body are totally different properties.
The mass m of a body is a scalar; its SI unit the kilogram. The mass of
a body can be determined by comparing it to the standard kilogram. Mass is an
intrinsic property of a body; it is the same on the earth's surface, in an
orbiting satellite, on Mars, or in interstellar space. The weight
 of a body is a vector; its SI unit in the Newton. The weight of a body with
mass m is defined as:
of a body is a vector; its SI unit in the Newton. The weight of a body with
mass m is defined as:
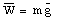
where g is the free-fall acceleration at the location of the body. Since the free-fall acceleration varies from point to point, the weight of an object depends on its location, and is therefore not an intrinsic property of a body.
The mass of a body can be determined via comparison with the standard mass. The equal-arm balance is designed for this purpose (see Figure 5.4). The equal-arm balance is balanced if the force on the left equals the force on the right:
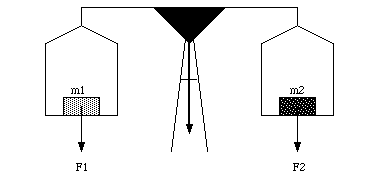
Figure 5.4. Equal-Arm Balance.
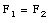
These two forces are the gravitational forces acting on m1 and m2 and can be calculated easily:
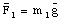
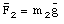
If the free-fall acceleration is constant at the location of the balance, we can conclude that if the arms are balanced:
m1 = m2
Therefore, the equal-arm balance determines the relative mass of two objects by comparing their weight.
The measurement of the weight of an object can be carried out using a spring scale (see Figure 5.5). The spring scale uses a spring to measure the weight of the object. There is a one-to-one relation between the stretch of the spring and the applied force (responsible for the stretch). In general, spring scales are calibrated and show the mass of the object. However, it should be stressed that the mass of the object is obtained from the measured weight, and in this process it is assumed that the free-fall acceleration equals 9.8 m/s2. Therefore, a spring scale will only indicate the correct mass if it is used at a location at which the free-fall acceleration is equal to that at the calibration site (note: a spring scale will incorrectly determine the mass of an object if it is used on the moon, or in an accelerating elevator).
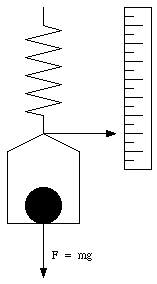
Figure 5.5. Spring Scale.
Sample Problem 5-7
Figure 5.6 shows a block of mass m = 15 kg hanging from three cords. What are the tensions in these cords ?
The mass m experiences a gravitational force equal to mg. Since the mass is at rest, cord C must provide an opposing force equal to mg. Applying Newton's third law, we conclude that cord C exerts a force on the knot whose magnitude is equal to mg (and pointed in the direction shown in Figure 5.6). Since the system is at rest, the net force on the knot must be equal to zero:
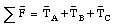
This vector equation can be rewritten in terms of its components along the x-axis and y-axis, using the following information:
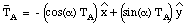
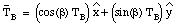
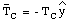
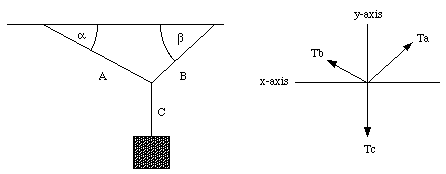
Figure 5.6. Sample Problem 5-7.
Using these expressions we can write down the equations for the x and y-components of the net force:
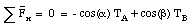
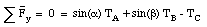
The first expression can be used to express TA in terms of TB:
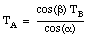
Substituting this expression into the equation for [Sigma]Fy we obtain:
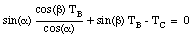
from which we can calculate TB:
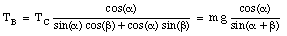
Knowing TB, we can now calculate TA:
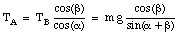
In the case of sample problem 5-6, the tensions in the cords are:
TA = 100 N
TB = 140 N
TC = 150 N
Problem
Figure 5.7 shows a block with mass m on a frictionless plane, tilted by an angle [theta]. What is the acceleration of the block ?
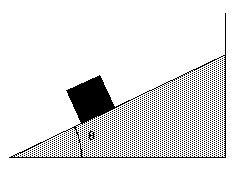
Figure 5.7. Mass m on an inclined plane.
In order to determine the acceleration of the block we have to determine the total force acting on the block along the inclined plane. Two forces act on the block: the gravitational force exerted by the earth on the block, and a force, called the normal force exerted by the plane on the block (see Figure 5.8). This force must be present since in its absence mass m will experience free fall (instead of sliding motion). Since the normal force is normal to the inclined plane it does not have a component along it. The component of the gravitational force along the inclined plane is given by

The acceleration produced by this force can be determined from Newton's second law
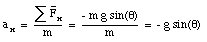
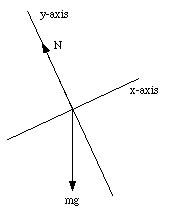
Figure 5.8. Forces acting on mass m.
Sample Problem 5-8
Figure 5.9 shows a block with mass m held by a cord on a frictionless plane, tilted by an angle [theta]. What is the tension in the cord ? What force does the plane exert on the block ?
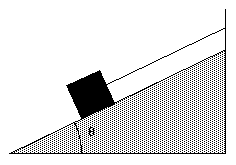
Figure 5.9. Sample Problem 5-8.
This problem can be solved easily if the coordinate system is chosen carefully. The best choice of coordinate system is shown in Figure 5.10. Since the block is at rest, the net force on it must be zero:
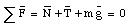
Due to the choice of the coordinate system, both N and T only have components along the y-axis and x-axis, respectively:
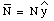
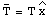
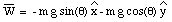
The mass will stay at rest if all components of the net force are zero:
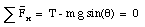

From these equations we can obtain N and T:
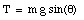
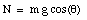
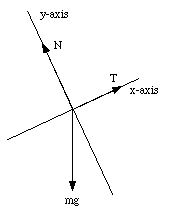
Figure 5.10. Coordinate System # 1 used in Sample Problem 5-8.
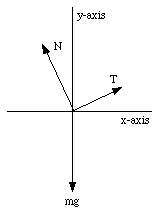
Figure 5.11. Coordinate System # 2 used in Sample Problem 5-8.
The standard choice of coordinate system with the x-axis coinciding with the horizontal direction and the y-axis coinciding with the vertical direction (see Figure 5.11) would have made the problem significantly more difficult. In this coordinate system, N and T have component along both the x and y direction:
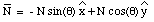
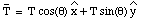
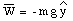
In this case, N and T can be obtained by solving the following equations:
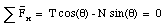
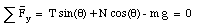
Of course, the solutions for N and T are identical to those derived previously, but the derivation is harder.
Sample Problem 5-10
Two blocks are connected by a cord that passes over a (weightless) pulley (see Figure 5.12). Find the tension in the cord and the (common) acceleration.
The blocks are moving with a constant acceleration. Since the cord is assumed to rigid, the acceleration of mass m has to be equal to the acceleration of mass M. However, since the pulley reverses the direction of motion, the direction of the acceleration of mass m is opposed to the direction of the acceleration of mass M. For each of the masses we can write down the following force equations:
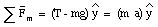
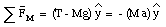
The first equation can be used to express T in terms of a:
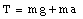
Substituting this expression for T into the second equation, we obtain:
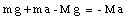
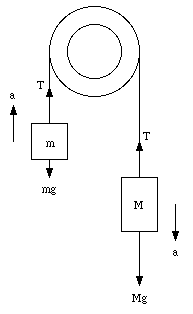
Figure 5.12. Setup Sample Problem 5-10.
The acceleration a can now be calculated:
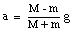
Note that a is positive when M > m, and a is negative when M < m. The acceleration is zero if m = M. This of course agrees with what our expectations. The tension in the cord can now be calculated:
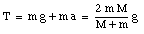
Problem
A block of mass m1 on a smooth inclined plane of angle [theta] is connected by a cord over a small frictionless pulley to a second block of mass m2 hanging vertically (see Figure 5.13). The mass of the cord and the pulley can be neglected.
a) What is the acceleration of each block ?
b) What is the tension in the cord ?
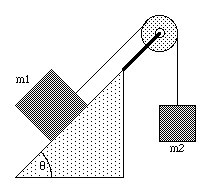
Figure 5.13. Inclined plane and pulley.
In order to determine the acceleration and the tension, we have to identify all forces acting on both masses. The following forces act on m1 (see Figure 5.14):
* The gravitational force W1 = m1 g. This force is
pointing downwards in the vertical direction.
* The normal force N. This force is exerted by the surface of the inclined
plane on the mass and is pointing in a direction perpendicular to the inclined
it.
* Tension T. The cord exerts this force on the mass. Its direction is
parallel to the inclined plane.
In general, the net force acting on m1 will be non-zero and m1 will have a non-zero acceleration. The acceleration will be along the x-axis (see Figure 5.14) and is defined to be positive if the acceleration is in the same direction as the tension T. The components of the net force acting on m1 are given by
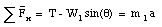
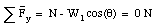

Figure 5.14. Forces acting on m1.
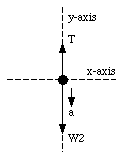
Figure 5.15. Forces acting on m2.
The following forces act on m2 (see Figure 5.15):
* The gravitational force W2 = m2 g. This force is
pointing downwards along the vertical.
* The tension T. The cord exerts this force on the mass. This force is
pointing upwards along the vertical. The tension in the cord is the same at
each point, and the magnitude of this force is therefore equal to the one
acting on m1 although it points in a different direction.
The net force on m2 will be non-zero and the mass will accelerate. Since m1 and m2 are connected via a cord, they will have the same acceleration. If the direction of the acceleration of m1 is along T, the direction of the acceleration on m2 will be along W2 (see Figure 5.15). None of the forces acting on m2 has a component along the x-axis and we will therefore only consider the net force along the y-axis:
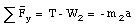
Equations (1) and (3) are two equations with two unknown (T and a), and can be solved. Equation (3) can be rewritten as
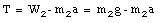
Substituting equation (4) for T in equation (1), we can determine a:
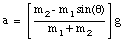
Substituting equation (5) into equation (4) we obtain the tension T: