In mechanics we are interested in trying to understand the motion of objects. In this chapter, the motion of objects in 1 dimension will be discussed. Motion in 1 dimension is motion along a straight line.
The position of an object along a straight line can be uniquely identified by its distance from a (user chosen) origin. (see Figure 2.1). Note: the position is fully specified by 1 coordinate (that is why this a 1 dimensional problem).
Figure 2.1. One-dimensional position.
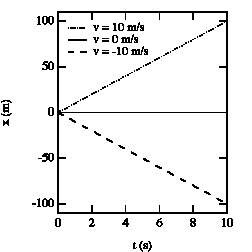
Figure 2.2. x vs. t graphs for various velocities.
For a given problem, the origin can be chosen at whatever point is convenient. For example, the position of the object at time t = 0 is often chosen as the origin. The position of the object will in general be a function of time: x(t). Figure 2.2. shows the position as a function of time for an object at rest, and for objects moving to the left and to the right.
The slope of the curve in the position versus time graph depends on the velocity of the object. See for example Figure 2.3. After 10 seconds, the cheetah has covered a distance of 310 meter, the human 100 meter, and the pig 50 meter. Obviously, the cheetah has the highest velocity. A similar conclusion is obtained when we consider the time required to cover a fixed distance. The cheetah covers 300 meter in 10 s, the human in 30 s, and the pig requires 60 s. It is clear that a steeper slope of the curve in the x vs. t graph corresponds to a higher velocity.
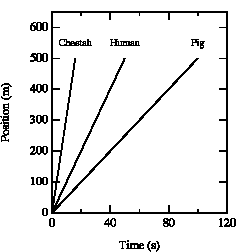
Figure 2.3. x vs. t graphs for various creatures.
An object that changes its position has a non-zero velocity. The average
velocity
 of an object during a specified time interval is defined as:
of an object during a specified time interval is defined as:
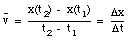
If the object moves to the right, the average velocity is positive. An
object moving to the left has a negative average velocity. It is clear from
the definition of the average velocity that
 depends only on the position of the object at time t = t1 and at
time t = t2. This is nicely illustrated in sample problem 2-1
and 2-2.
depends only on the position of the object at time t = t1 and at
time t = t2. This is nicely illustrated in sample problem 2-1
and 2-2.
Sample Problem 2-1
You drive a beat-up pickup truck down a straight road for 5.2 mi at 43 mi/h, at which point you run out of fuel. You walk 1.2 mi farther, to the nearest gas station, in 27 min (= 0.450 h). What is your average velocity from the time you started your truck to the time that you arrived at the station ?
The pickup truck initially covers a distance of 5.2 miles with a velocity of 43 miles/hour. This takes 7.3 minutes. After the pickup truck runs out of gas, it takes you 27 minutes to walk to the nearest gas station which is 1.2 miles down the road. When you arrive at the gas station, you have covered (5.2 + 1.2) = 6.4 miles, during a period of (7.3 + 27) = 34.3 minutes. Your average velocity up to this point is:
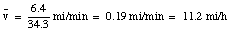
Sample Problem 2-2
Suppose you next carry the fuel back to the truck, making the round-trip in 35 min. What is your average velocity for the full journey, from the start of your driving to you arrival back at the truck with the fuel ?
It takes you another 35 minutes to walk back to your car. When you reach your truck, you are again 5.2 miles from the origin, and have been traveling for (34.4 + 35) = 69.4 minutes. At that point your average velocity is:
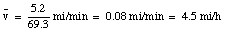
After this episode, you return back home. You cover the 5.2 miles again in 7.3 minutes (velocity equals 43 miles/hour). When you arrives home, you are 0 miles from your origin, and obviously your average velocity is:
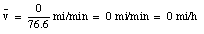
The average velocity of the pickup truck which was left in the garage is also 0 miles/hour. Since the average velocity of an object depends only on its initial and final location and time, and not on the motion of the object in between, it is in general not a useful parameter. A more useful quantity is the instantaneous velocity of an object at a given instant. The instantaneous velocity is the value that the average velocity approaches as the time interval over which it is measured approaches zero:
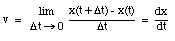
For example: see sample problem 2-5.
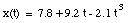
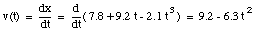
The velocity of the object at t = 3.5 s can now be calculated:
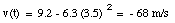
The velocity of an object is defined in terms of the change of position of that object over time. A quantity used to describe the change of the velocity of an object over time is the acceleration a. The average acceleration over a time interval between t1 and t2 is defined as:
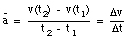
Note the similarity between the definition of the average velocity and the definition of the average acceleration. The instantaneous acceleration a is defined as:
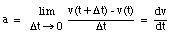
From the definition of the acceleration, it is clear that the acceleration has the following units:
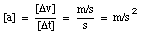
A positive acceleration is in general interpreted as meaning an increase in velocity. However, this is not correct. From the definition of the acceleration, we can conclude that the acceleration is positive if
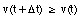
This is obviously true if the velocities are positive, and the velocity is increasing with time. However, it is also true for negative velocities if the velocity becomes less negative over time.
Objects falling under the influence of gravity are one example of objects moving with constant acceleration. A constant acceleration means that the acceleration does not depend on time:
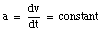
Integrating this equation, the velocity of the object can be obtained:
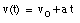
where v0 is the velocity of the object at time t = 0. From the velocity, the position of the object as function of time can be calculated:
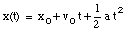
where x0 is the position of the object at time t = 0.
Note 1: verify these relations by integrating the formulas for the position and the velocity.
Note 2: the equations of motion are the basis for most problems (see sample problem 7).
Sample Problem 2-8
Spotting a police car, you brake a Porsche from 75 km/h to 45 km/h over a distance of 88m. a) What is the acceleration, assumed to be constant ? b) What is the elapsed time ? c) If you continue to slow down with the acceleration calculated in (a) above, how much time would elapse in bringing the car to rest from 75 km/h ? d) In (c) above, what distance would be covered ? e) Suppose that, on a second trial with the acceleration calculated in (a) above and a different initial velocity, you bring your car to rest after traversing 200 m. What was the total braking time ?
a) Our starting points are the equations of motion:
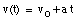
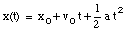
The following information is provided:
* v(t = 0) = v0 = 75 km/h = 20.8 m/s
* v(t1) = 45 km/h = 12.5 m/s
* x(t = 0) = x0 = 0 m (Note: origin defined as position of Porsche at t = 0 s)
* x(t1) = 88 m
* a = constant
From eq.(1) we obtain:
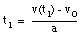
Substitute (3) in (2):
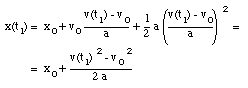
From eq.(4) we can obtain the acceleration a:
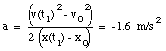
b) Substitute eq.(5) into eq.(3):
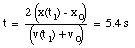
c) The car is at rest at time t2:
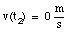
Substituting the acceleration calculated using eq.(5) into eq.(3):
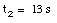
d) Substitute t2 (from eq.(8)) and a (from eq.(5)) into eq.(2):
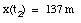
e) The following information is provided:
* v(t3) = 0 m/s (Note: Porsche at rest at t = t3)
* x(t = 0) = x0 = 0 m (Note: origin defined as position of Porsche at t = 0)
* x(t3) = 200 m
* a = constant = - 1.6 m/s2
Eq.(1) tells us:
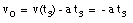
Substitute eq.(10) into eq.(2):
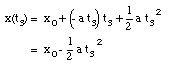
The time t3 can now easily be calculated:
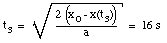
A special case of constant acceleration is free fall (falling in vacuum). In problems of free fall, the direction of free fall is defined along the y-axis, and the positive position along the y-axis corresponds to upward motion. The acceleration due to gravity (g) equals 9.8 m/s2 (along the negative y-axis). The equations of motion for free fall are very similar to those discussed previously for constant acceleration:
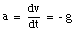
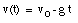
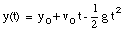
where y0 and v0 are the position and the velocity of the object at time t = 0.
Example
A pitcher tosses a baseball straight up, with an initial speed of 25 m/s. (a) How long does it take to reach its highest point ? (b) How high does the ball rise above its release point ? (c) How long will it take for the ball to reach a point 25 m above its release point.
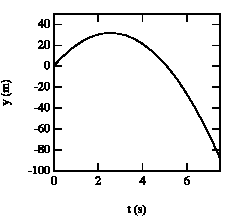
Figure 2.4. Vertical position of baseball as function of time.
a) Our starting points are the equations of motion:
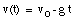
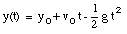
The initial conditions are:
* v(t = 0) = v0 = 25 m/s (upwards movement)
* y(t = 0) = y0 = 0 m (Note: origin defined as position of ball at t = 0)
* g = 9.8 m/s2
The highest point is obtained at time t = t1. At that point, the velocity is zero:
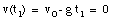
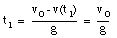
The ball reaches its highest point after 2.6 s (see Figure 2.4).
b) The position of the ball at t1 = 2.6 s can be easily calculated:
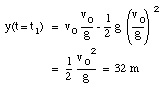
c) The quation for y(t) can be easily rewritten as:
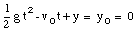
where y is the height of the ball at time t. This Equation can be easily solved for t:
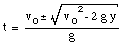
Using the initial conditions specified in (a) this equation can be used to calculate the time at which the ball reaches a height of 25 m (y = 25 m):
t = 1.4 s
t = 3.7 s
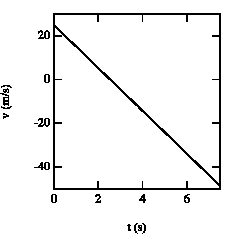
Figure 2.5. Velocity of the baseball as function of time.
The velocities of the ball at these times are (see also Figure 2.5):
v(t = 1.4 s) = + 11.3 m/s
v(t = 3.7 s) = - 11.3 m/s
At t = 1.4 s, the ball is at y = 25 m with positive velocity (upwards motion). At t = 2.6 s, the ball reaches its highest point (v = 0). After t = 2.6 s, the ball starts falling down (negative velocity). At t= 3.7 s the ball is located again at y = 25 m, but now moves downwards.