Physics 121, Final Exam
Do not turn the pages of the exam until
you are instructed to do so.
You are responsible for reading the following rules
carefully before beginning.
Exam rules: You may
use only a writing instrument while
taking this test.
You may not
consult any calculators, computers, books, notes, or each other.
Procedure:
1. Answer the multiple-choice questions (problems 1 – 10) by marking your answer on the scantron form. For each multiple-choice question (problems 1 – 10), select only one answer. Questions with more than one answer selected will be considered incorrect.
2. The analytical problems (11 – 18) must be answered in the blue exam booklets. You must answer problems 11, 12, and 13 in booklet 1, problems 14, 15, and 16 in booklet 2, and problems 17 and 18 in booklet 3. If you do not follow this convention there is no guarantee that the problems that appear in the wrong booklet will be graded.
3. The answer to each analytical problem must be well motivated and expressed in terms of the variables used in the problem. You will receive partial credit where appropriate, but only when we can read your solution. Answers that are not motivated will not receive any credit, even if correct.
4. At the end of the exam, you must hand in the blue exam
booklets, the scantron form, the exam, and the formula sheets. All items must be clearly labeled with
your name and student ID number. If
any of these items is missing, we will not grade your exam, and you will
receive a score of 0 points.
Note: If you do not
answer a question in terms of the variables provided, you will not receive
credit for that question.
Note: Your grade on the final
exam will be based on the numerical sum of the score for the multiple-choice
questions (25 points) and the sum of the scores of 7 best analytical questions
(we will drop the worst result on the analytical questions from the final exam
grade) .
Problem 1 (2.5 points)
Two blocks of the same size but different masses, m1 and m2, are placed on a table side-by-side in contact with each other. Assume that m1 > m2. Let N1 be the normal force between the two blocks when you push horizontally on the free side of m1 (towards m2). Let N2 be the normal force between the two blocks when you push horizontally on the free side of m2 (towards m1). Which of the following statements is true?
1. N1 = N2
2. N1 < N2
3. N1 > N2
Problem 2 (2.5 points)
A ball slides down an inclined track and then rounds a loop-the-loop. The ball is released from an initial height so that it has just enough speed to go around the loop without falling off. At the top of the loop-the-loop, the normal force of the loop on the ball is
1. equal to the weight of the ball and pointing down.
2. equal to the weight of the ball and pointing up.
3. equal to twice the weight of the ball and point up.
4. equal to zero.
Problem 3 (2.5 points)
What is the force that corresponds to the potential energy function U(x, y) = 3xy + 5x2 + 6y3?
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Problem 4 (2.5 points)
Three uniform spheres of radii 2R, R, and 3R are placed in contact next to each other on the x axis in this order (the smallest sphere is in the center, the 2R sphere is located to the left, and the 3R sphere is located to the right). The centers of the spheres are located on the x axis. What is the distance from the center of mass of this system from the center of the smallest sphere, assuming that each sphere has the same density?
1. (7/3)R
2. (1/3)R
3. (3/7)R
4. (65/36)R
Problem 5 (2.5 points)
The precession rate of the a spinning top
1. is proportional to its angular momentum
2. does not depend upon its angular momentum
3. is inversely proportional to its angular momentum
4. is inversely proportional to its kinetic energy
Problem 6 (2.5 points)
For most materials, how is the coefficient of volume
expansion related to the coefficient of linear expansion?
1. The coefficient of volume expansion is equal to the
coefficient of linear expansion.
2. The coefficient of volume expansion is one-third the
coefficient of linear expansion.
3. The coefficient of volume expansion is three times the
coefficient of linear expansion.
4. The coefficient of volume expansion is twice the
coefficient of linear expansion.
Problem 7 (2.5 points)
|
1 |
2 |
3 |
4 |
Match the above shown players with the
following names:
|
A.
Manny Ramirez |
C.
Daisuke Matsuzaka |
|
B.
Jason Varitek |
D.
David Ortiz |
1234 =
1.
ABCD
2.
ACDB
3.
BADC
4.
BDAC
5.
CADB
6.
CABD
7.
DBAC
8. DCBA
Problem 8 (2.5 points)
Consider the following graph, showing position versus time for simple harmonic motion.
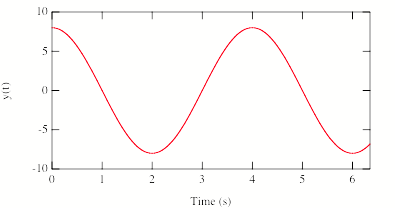
What is the frequency of this motion?
1. 0.25 Hz
2. 0.50 Hz
3. 1.0 Hz
4. 4.0 Hz
Problem 9 (2.5 points)
By what factor does the RMS speed of an ideal gas
change when the absolute temperature of the gas is doubled?
1. 2
2. 4
3. ½
4. Ã2
Problem
10 (2.5
points)
A system consisting of a fixed amount of gas starts at
pressure P1 and
volume V1 and
ends up at pressure P2
and volume V2
after some thermodynamic process.
Which of the following quantities do not depend on the path taken on a
pressure–volume diagram during the process?
1. Work done on the environment by the system during the
process.
2. Work done by the environment on the system during the
process.
3. The heat added to the system during the process.
4. The final temperature of the system.
Problem 11 (25 points) Answer in Exam Booklet 1
The operation of an automobile internal combustion engine can be approximated by a reversible cycle known as the Otto cycle, whose PV diagram is shown in the Figure below. The gas in cylinder at point a is compressed adiabatically to point b. Between point b and point c, heat is added to the gas, and the pressure increases at constant volume. During the power stroke, between point c and point d, the gas expands adiabatically. Between point d and point a, heat is removed from the system, and the pressure decreases at constant volume. Assume the gas is an ideal monatomic gas.
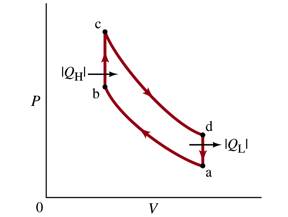
(a) Assuming there are n moles of gas in system, what are the heats |QH| and |QL|? Express your answer in terms of n, R, Ta, Tb, Tc, and Td.
(b) What is the efficiency of the Otto cycle? Express your answer in terms of Ta, Tb, Tc, and Td.
(c) Express the efficiency of the Otto cycle in terms of just the compression ratio Va/Vb and g. Hint: use the fact that during an adiabatic process PVg = constant.
(d) How does the efficiency change when we replace the monatomic gas with a diatomic gas?
Problem 12 (25 points) Answer in Exam Booklet 1
A tunnel is bored through the Earth along a diameter, as shown in the Figure below. Assume that the earth is a homogeneous sphere with total mass M and radius R.
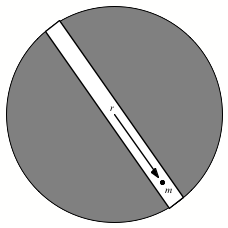
(a) A package with mass m is dropped into the tunnel. Use the shell theorem to calculate the gravitational force acting on the package as function of the distance r from the center of the Earth.
(b) Show that the package will oscillate back and forth with simple harmonic motion.
(c) If the tunnel were used to deliver mail, how long would it take for a letter to travel through the Earth?
Express all your answer in terms of G, m, M, r, and R.
A thin horizontal bar AB of mass m and length L is
pinned to a vertical wall at A and supported at B by a thin wire BC that makes
and angle q with the horizontal.
A block with mass M can be moved
anywhere along the bar. The
distance x is defined as the distance
between the center of mass of the block and the wall (see Figure). The system is in equilibrium.
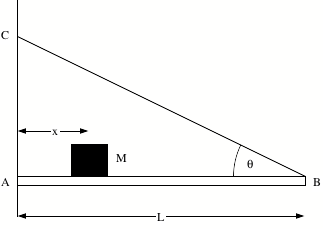
(a) What is the
tension in the thin wire as function of x?
(b) What is the
horizontal component of the force exerted on the bar by the pin at A as
function of x?
(c) What is the
vertical component of the force exerted on the bar by the pin at A as function
of x?
Express all you answers in terms of
m, M, x, L, q, and g.
A bullet of mass m is fired horizontally at two blocks resting on a smooth
table top, as shown in the Figure.
The bullet passes through the first block of mass M1, and embeds itself in a second block of mass M2.
Speeds equal to v1
and v2, respectively, are
thereby imparted on the blocks, as shown in the Figure. The mass removed from the first block
by the bullet can be neglected.
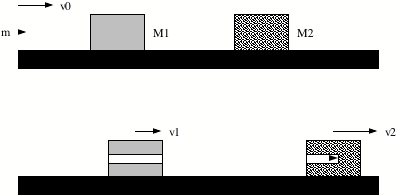
(a) What is the
speed of the bullet immediately after emerging from the first block?
(b) What is the
original speed of the bullet?
(a) A car of
mass m moves at a constant speed v0 on a curved unbanked roadway whose radius of
curvature is equal to R. The car is able to make the turn
without skidding of the road. What
must be the minimum coefficient of static friction µs
between the tires and the roadway?
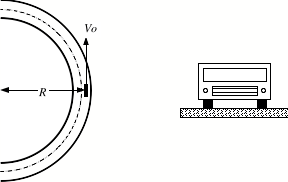
(b) You cannot count
on a sideways frictional force to get your car around a curve if the road is
icy or wet. That is why highways
are banked. Suppose a car of mass m moves at a constant speed v on a curved banked highway whose radius of curvature is
equal to R and whose angle of bank is
equal to q. There is no
friction between the tires and the roadway. What speed must the car have in order to round the curve
without skidding of the road?
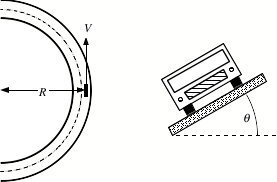
Express all your answers in terms of m, R, q, v0, and g.
Problem 16 (25 points) Answer in Exam Booklet 2
A hoop of mass M and radius R is
rolling down a ramp that slopes at an angle q (see
Figure). The hoop starts from
rest, a distance L up the slope, and
rolls without slipping. The entire
mass of the hoop is distributed uniformly along its rim.
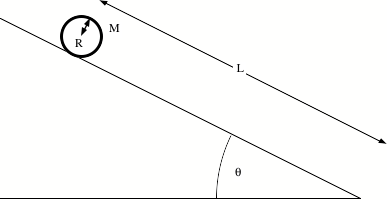
(a) What is the
friction force f between the hoop and
the surface of the slope?
(b) What is the linear
acceleration of the rolling hoop?
(c) How long
does it take the hoop to reach the bottom of the ramp?
(d) What is the
velocity of the hoop at the bottom of the ramp?
(e) What happens
if there is no friction between the ramp and the hoop?
Express all your answers in terms of M, R, q, L, and g.
Consider a composite slab of
material of cross-sectional area A,
consisting of two materials having different thicknesses, L1 and L2,
and different thermal conductivities, k1
and k2. The temperatures of their outer
surfaces are Th and Tc.
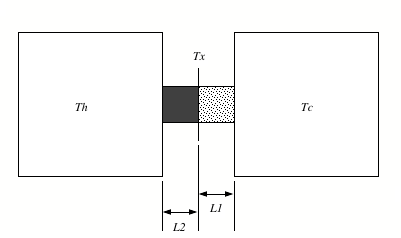
a) What is
the temperature Tx at the
interface between the two materials of the slab?
b) Calculate
the rate of heat transfer through this composite slab.
Problem
18 (25 points) Answer
in Exam Booklet 3
A rigid rod of mass M and length L
rotates in a vertical plane about a frictionless pivot through its center (see
Figure). Two solid spheres of
masses m1 and m2 are attached to the ends of the rod. Assume m1 > m2.
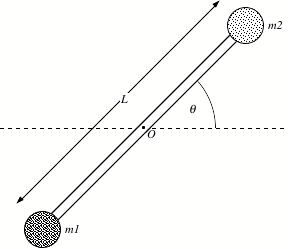
a) Determine
the angular momentum of the system when the angular velocity is equal to w.
b) Determine
the magnitude of the angular acceleration of the system when the rod makes an
angle q with the horizontal.
Express all your answers in terms
of m1, m2, M, L, q, and w



