Physics 121, Midterm Exam #2

Tuesday March 25, 2008

8.00 am – 9.30 am

 

Do not turn the pages of the exam until you are instructed to do so.

 

You are responsible for reading the following rules carefully before beginning.

Exam rules: You may use only a writing instrument while taking this test.  You may not consult any calculators, computers, books, nor each other.

Answer the multiple-choice questions (problems 1 – 10) by marking your answer on the scantron form.  For each multiple-choice question (problems 1 – 10), select only one answer.  Questions with more than one answer selected will be considered incorrect.  Problems 11, 12, and 13 must be answered in the blue exam booklets and need to be well motivated and expressed in terms of the variables used in the problem.  Answer questions 11 and 12 in booklet # 1 and question 13 in booklet # 2.  You will receive partial credit where appropriate, but only when we can read your solution.  Answers that are not motivated will not receive any credit, even if correct.

At the end of the exam, you need to hand in your exam, the blue exam booklets, and your scantron form.  All items must be clearly labeled with your name and student ID number.  If any of these items is missing, we will not grade your exam, and you will receive a score of 0 points.

 

Name:  __________________________________________________

 

ID number:  ______________________________________________

 

Workshop Day/Time:  ______________________________________

Intentionally left blank

Problem 1 (2.5 points)

A force acting on an object accelerates it up to a speed v after starting from rest.  Does accelerating to that speed in a shorter time increase or decrease the amount of work done by the force?

  1. Shorter time means a bigger force so more work is done.
  2. Shorter time means the car travels a shorter distance so less work is done.
  3. Same change in kinetic energy regardless of time, so the same amount of work is done.
  4. More information is needed to answer the question.

 

Problem 2 (2.5 points)

An object moves around a closed path so its displacement for the entire motion is zero.  Can you conclude that the work done is zero?

  1. Yes, no displacement implies no work.
  2. No, the work done in going around a closed path is always negative.
  3. No, the work done in going around a closed path is always positive.
  4. Not enough information is given to determine whether the work is zero, positive, or negative.

 

Problem 3 (2.5 points)

Can an object have a net negative work done on it with a magnitude greater than its kinetic energy?

  1. Yes, there is no limit to the amount of work done on the object.
  2. No, once the kinetic energy is brought to zero, no more negative work can be done on the object.

 

Problem 4 (2.5 points)

An object on which a constant force F is acting starts from rest and reaches a speed v after a distance d.  What force is required to increase its speed from zero to 2v in a distance 2d?

  1. F/2
  2. F/4
  3. 2F
  4. 4F

 

Problem 5 (2.5 points)

Two people on roller blades throw a ball back and forth.  After a couple of throws, they are

1.     Standing where they were initially.

2.     Standing further away from each other.

3.     Moving away from each other.

4.     Moving towards each other.

 

Problem 6 (2.5 points)

A cart on an air track is moving at 0.5 m/s when the air is suddenly turned off.  The cart comes to rest after traveling 1 m.  The experiment is repeated, but now the same cart is moving at 1 m/s when the air is turned off.  How far does the cart now travel before coming to rest?

1.     1 m.

2.     2 m.

3.     3 m.

4.     4 m.

5.     5 m.

6.     Impossible to determine.

 

Problem 7 (2.5 points)

Two carts are put back-to-back on a track.  Cart A has a spring-loaded piston; cart B, which has twice the inertial mass of cart A, is entirely passive.  When the piston is released, cart A pushes against cart B, and the carts move apart.  How do the magnitudes of their final momenta p and kinetic energies K compare?

1.     pA > pB, KA > KB.

2.     pA > pB, KA = KB.

3.     pA > pB, KA < KB.

4.     pA = pB, KA > KB.

5.     pA = pB, KA = KB.

6.     pA = pB, KA < KB.

7.     pA < pB, KA > KB.

8.     pA < pB, KA = KB.

9.     pA < pB, KA < KB.

 

Problem 8 (2.5 points)

The linear density of a long thin rod, of length L, decreases from a value of d at the left end to zero at the right end.  How far from the left end is the rodŐs center-of-mass located?

  1. L/5
  2. L/3
  3. (2/3) L
  4. (4/5) L

 

Problem 9 (2.5 points)

Which of the following units may be used to describe linear momentum?

  1. Ns
  2. N/s
  3. Nm
  4. N/m

 

Problem 10 (2.5 points)

 

1

2

3

4

Match the above shown players of the best baseball team in the world with the following names:

A.  Jose Molina

C.  Bobby Abreu

B.  Derek Jeter

D.  Joba Chamberlain

1234 =

1.     ABCD

2.     ACDB

3.     BADC

4.     BDAC

5.     CADB

6.     CABD

7.     DBAC

8.     DCBA

Problem 11  (25 points)                                                                         Answer in Exam Booklet 1

A ball of mass m is projected with speed vi into the barrel of a spring gun of mass M, initially at rest on a frictionless surface (see Figure below).  The ball sticks in the barrel at the point of maximum compression of the spring.  No energy is lost due to friction.

 

 

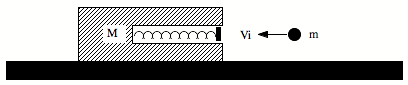
a)   What is the speed of the spring gun after the ball comes to rest in the barrel?

b)   What fraction of the initial kinetic energy of the ball is stored in the spring?

 

Express all your answers in terms of m, M, and vi.

 

Problem 12  (25 points)                                                                         Answer in Exam Booklet 1

A steel ball of mass m is fastened to a cord of length L and is released when the cord is horizontal (see Figure).  At the bottom of its path the ball strikes a block of mass M (M > m), initially at rest.  The kinetic friction coefficient between the block and the surface is equal to µk (neglect static friction).  The collision is elastic.

 

 

 

 

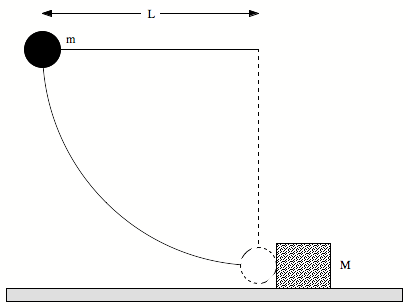
a)   Find the velocity of the ball just before the collision.

b)   What is the tension in the cord just before the collision?

c)   Find the velocity of the ball and block just after the collision.

d)   What is the tension in the cord just after the collision?

e)   What is the maximum height the ball reaches after the collision?

f)   Calculate the distance traveled by the block before coming to rest.

 

Express all your answers in terms of m, M, L, g, and µk.

 

Problem 13  (25 points)                                                                         Answer in Exam Booklet 2

A small block of mass m slides along a frictionless loop-the-loop track as shown in the Figure below.  The block is released from rest at point P.

 

 

 

 

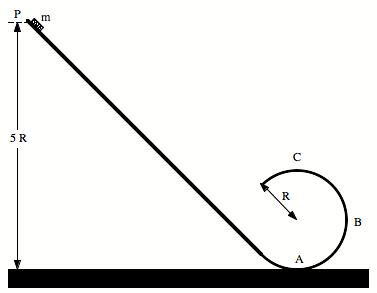
a)   Draw a force diagram of all forces acting on the block at point A.

b)   What is the velocity of the block at point A?

c)   Draw a force diagram of all forces acting on the block at point B.

d)   What is the net force acting on the block at point B?  Specify the magnitude and the direction of the net force.

e)   At what height above the bottom of the loop should the block be released so that it is in the verge of losing contact with the track at the top of the loop (point C)?

 

Express all your answers in terms of m, g, and R.

SCRATCH PAPER

SCRATCH PAPER

SCRATCH PAPER

SCRATCH PAPER

Geometry/Trigonometry:

 

 

 

 

 

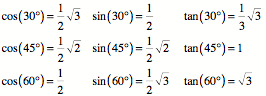
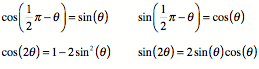
Integrating and Differentiating:

 

 

 

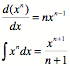
Linear Motion in One Dimension (general):

 

 

 

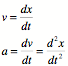
Linear Motion in One Dimension (special case):

 

 

 

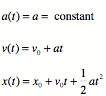
Linear Motion in Two/Three Dimensions:

 

 

 

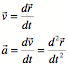
Circular Motion:

 

 

 

Force Laws:

 

 

 

Friction:

 

 

 

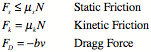
NewtonŐs Gravitational Law:

 

 

 

KeplerŐs Third Law (Law of Periods):

 

 

 

Work Done by a Force:

 

 

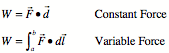
Translation Kinetic Energy:

 

 

Work-Energy Theorem:

 

 

Potential Energy:

 

 

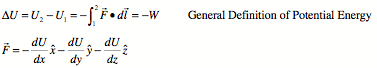
Conservation of Energy:

 

 

Power:

 

 

Linear Momentum and NewtonŐs Second Law:

 

 

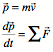
Collision Impulse:

 

 

Elastic Collisions in One Dimension:

 

 

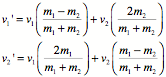
Center of Mass:

 

 

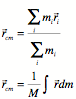
Motion of the Center of Mass:

 

 

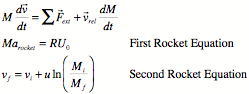
Rocket Equations: