The Physics of the Soda Can Crumple Zone

May 5, 2003 ^˜ PHYSICS BY INQUIRY

By: Dan Bobkoff and Kelly McNamee

Abstract

Collisions are a fact of life. People walk into others on the street. Cars crash into each other. Molecules collide. Every collision is physics in action. In our class, we created controlled collisions to measure the effects of motion and energy in such cases. We crashed rolling carts with students on them into each other. Standardized, emptied soda cans mounted on the front of the vehicles absorbed the energy.

In completing this exercise, we found that the energy required to deform the cans is directly proportional to the level of deformation squared.

Theory

Momentum is conserved in collisions, whereas some energy is always lost. This is the expected and found conclusion of a day’s worth of collision and days of analysis. Momentum is the speed (velocity) of an object multiplied by the mass and taking into account direction. The formula for energy is (0.5)mv². This formula is useful in determining the loss of energy in such collisions.

Experiment

The experiment commenced on the University of Rochester quad where we set up two identical carts with four identical empty soda cans securely mounted on the front of each. The carts are positioned at opposite ends of a straight track with the cans opposing each other. A member of the class sat on each cart, and a member was assigned to push the students as necessary. Each student was weighed and each can was measured before and after the deformation.

We carried out a variety of collision situations. Some sent the carts towards each other at varying rates. Others left one cart at rest, while the other was pushed into it. Each collision was videotaped in the same manner for later analysis.

Analysis was completed over several days. Using special software called VideoPoint, we established the velocities before and after the collisions for each cart. The software works by having the user tell the computer a fixed distance on the image to use as a reference. Then, for each frame of the video, the experimenter tells the computer the amount the cart moved. This is done by clicking on a part of the cart that moves. The same part of the cart must be used to get accurate results. For example, many clicked on the front wheels. The computer then produced tables and graphs from the result. The process is imperfect because of the limitations of the video and computer systems, and natural human error. From this data, we used formulas and extrapolation to find momentum and energy and analyzed using spreadsheet software.

Data Analysis

While VideoPoint is inexact, it does provide a multitude of information. It gives velocity data for every frame and every cart. The amount of data expands quickly. We, however, wished to look at only a small portion of the data—that being the information immediately before the collision between the two carts, and that immediately after the collision.

VideoPoint gave us a velocity graph for each of the carts. We pinpointed the three points before and after the collision and found an average for each. Two example graphs from Run #3 are shown below.

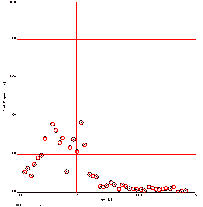
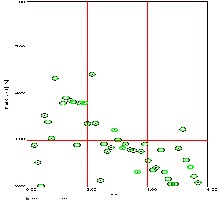
In most of the runs, more than one person analyzed the velocity information. Therefore, we had to find averages and error readings for velocity-initial of the right cart and velocity-initial of the left cart, as well as the final velocity of the left and right carts. We did this by first finding the averages and then, to find the error, we subtracted the smallest velocity of that category from the largest velocity and divided this result by 2.

Then we used these averages to find the initial momentum and final momentum of each run. The errors of each velocity were important when we had to find our momentum error calculations. First, the way we found momenta was to multiply mass by velocity. Since we had two different velocities and masses to work with when we were finding each momentum reading, we took mass₁multiplied by velocity₁ and added this to mass₂ multiplied by velocity₂. For example, in Run #3, our first run together, we found initial momentum by multiplying the initial velocity of the right cart (-1.524) by the mass of the right student (135) (note that the carts cancel each other out so their rate is moot) and added this result to the initial of the left cart (2.528) multiplied by the mass of the left student (174) to bring us to the initial momentum (234.113). The final momentum is calculated in the same manner using the final velocity in place of the initial. We then found the error of the momentum by finding out what the maximum momentum would be when we take into account the error in the velocity measures. This was subtracted from the minimum of the velocity measures. The answer was divided by 2 lending us our error measurement for momentum. We did this by finding momentum with velocities plus their errors, and then subtracting this by the result of finding momentum with velocities minus their errors. Then, we took this result and divided by 2 to find our momentum errors.

Because of the high level of error in our velocity results, and therefore our momentum results, it is difficult to state whether momentum is conserved or not. When forced to give an answer the best estimate we can provide is that momentum is conserved. We believe this is true because we see no reason for momentum not to be conserved and it is possible to say this within our error estimates.

Next, we found the initial kinetic energy, the final kinetic energy, and the loss of kinetic energy for each collision and the corresponding error reading for each. First we found the initial kinetic energy with this formula:

((0.5)mass_left*velocity_initial-left²) +((0.5)mass_right*velocity_{initial-right}²)

Final energy uses the same formula, except that it substitutes final velocities for the initial shown in this formula. The kinetic energy lost is found by taking the final kinetic energy and subtracting the initial final kinetic energy.

We found the error of the initial and final kinetic energy the same way. We used the same energy equation, but substituted the error of the velocity that corresponds to the velocity in the above formula:

((0.5)mass_left*error of velocity_initial-left²) +((0.5)mass_right*error of velocity_{initial-right}²)

We found the error of the kinetic energy lost by taking the maximum of what the error lost would be when taking into account the errors in the finals and initial kinetic energy. Then, we subtracted the minimum. This result was divided by 2 lending us our error:

MAX = (E_final + error) – (E_initial– error)

MIN = (E_final – error) – (E_initial+ error)

Error of Energy Lost =

(MAX – MIN) / 2

Then, we found out how much each can deformed in each collision. This was done by taking the standardized 10.4cm length measurement and subtracting the final measurements of the length of each can. We then added these measurements together to find the totals for each collision. This total was then squared. We found this total and squared it to try and find which of the two models we were given explained the relationship between the deformation of the cans and the loss of kinetic energy. One model was that the deformation of the cans had a linear relationship to the loss in kinetic energy. The second model was that the deformation of the can squared had a linear relationship to the loss of kinetic energy. To establish this, we graphed both the deformation versus the loss of kinetic energy and the total deformation squared versus the loss of kinetic energy. The charts are shown below.

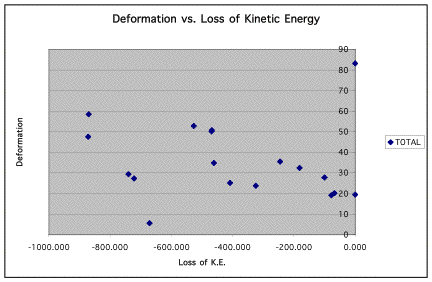
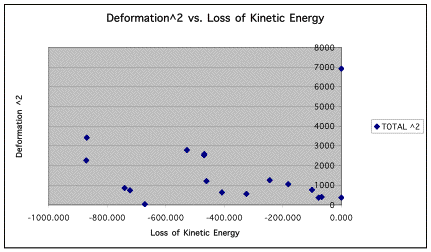
Although neither is a true linear relationship, the deformation²graph provides a more consistently measurable line that goes through the origin. Three points seem like outliers. These three points are the ones to the bottom left of the graph. They are inconsistent with the rest of the points because, as deformation increases, loss of kinetic energy should also increase. These points do not show this to be true. We could find no consistent error in calculations to explain this anomaly. The only reason we can attempt is that the more cans that were deformed in each collision, the better the data seems to be. These three runs, 1,3, and 9, had fewer deformed cans than other runs.

Accompanying this lab report is the spreadsheet containing all of our data.

Conclusion

As well as our equipment and experience can conclude, momentum does seem to be conserved in violent collisions between two objects. The loss of energy seems to be proportional to the deformation². A more accurate video and computer system would help further prove this finding, but with the large amount of data we worked with and the careful error calculations, we are fairly confident in standing by that result.

Remarks

This experiment was the culmination of weeks of hands-on physics education. This activity allowed us to be a real part of the experiment (quite literally) and then get practice analyzing large amounts of data in a manner that built on our past experiences in the class.