Graphs and the Scientific Method

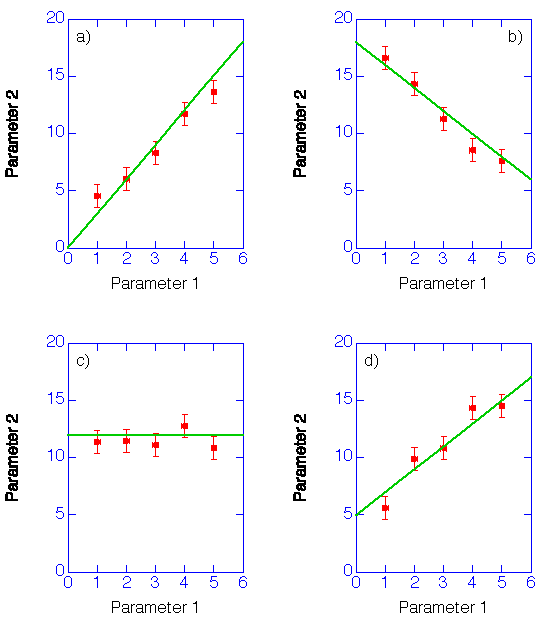
Graphs play a crucial role in many discoveries in basic science. Graphs are used as a tool to observe correlations between various experimental parameters. The simplest correlation between two experimental parameters is the linear correlation. If 2 parameters, parameter 1 and parameter 2, have a linear correlation, their graph can be described by a straight line. The following graphs all show parameters that have a linear correlation, although the nature of the correlation is different in each case.

These graphs have the following properties:

• Graph a. Data are described by a line that goes to the origin of the graph (parameter 1 = 0 and parameter 2 = 0). For such a relation between parameter 1 and parameter 2 you will observe that if you double parameter 1, you also double parameter 2. In example of such a relation is the relation between mass and volume: mass = density x volume. In this case you will observe that the ratio of parameter 1 and parameter 2 for each of the measurements shown is roughly constant (within the measurement errors).
• Graph b. This graph shows that parameter 2 decreases when parameter 1 increases. If parameter 1 is zero, parameter 2 is not zero, and clearly parameter 1 and parameter 2 are not proportional to each other (and their ratio is not constant).
• Graph c. This graphs shows that parameter 2 is constant (and independent) of parameter 1.
• Graph d. This graph shows that parameter 2 increases when parameter 1 increases. Although there is a linear dependence between parameter 1 and parameter 2, their ratio is not a constant.

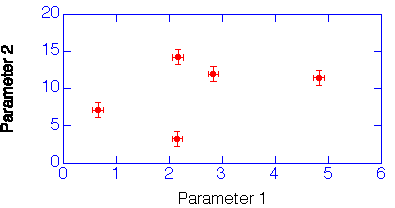
Of course, there does not always have to be a relation between two parameters. The following graph shows the results of a number of measurements which are uncorrelated.

Once a correlation is observed between parameters, the graph can be used to make predictions about the outcome of future measurements, as long as one of the two parameters is controlled by the experimenter. To get a feel for the accuracy with which you can make predictions based on an observed correlation, you can play around with the Applet below, which allows you to make predictions for different observed correlations between parameter 1 (in this case the horizontal distance x) and parameter 2 (in this case the vertical distance y).

To explore how to manipulate the parameters to be graphed in order to establish linear relations, you can carry out the following exercises.

• Measure the area of a disk.
• Relation between the orbital radius and the orbital period of the planets.

© Frank L. H. Wolfs, University of Rochester, Rochester, NY 14627, USA

Last updated on Sunday, February 11, 2001 21:52