Statistical Errors
Purpose
To understand statistical distributions and their appropriate errors by
calculating a binomial distribution and comparing it to the Poisson and
Gaussian (normal) distributions.
Introduction
Probability distributions are widely used primarily in experiments which
involve counting. The sampling errors which occur in counting experiments are
called statistical errors. Statistical errors are one special kind of error in
a class of errors which are known as random errors. You will find that
what you learn in this laboratory is relevant not only in the natural and
social sciences, but also in every day life. Please read the theory section
that follows, and then the file on Error Analysis before proceeding to
do the prelab. Bring the completed error analysis prelab with you.
This section will help the student with the prelab homework. You are probably
familiar with polls conducted before a presidential election. If the sample of
people who are polled is carefully chosen to represent the general population,
then the error in the prediction depends on the number of people in the sample.
The larger the number of people, the smaller the error. If the sample is not
properly chosen, it would result in a bias (i.e. an additional systematic
error).
If a fraction p of the population will vote Democratic and a fraction q
= (1-p) will vote Republican, then one expects that in a sample of N
people, one will find on average
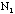 =
=
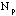 people who say that they will vote Democratic, and
people who say that they will vote Democratic, and
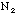 =
=
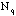 = N(1 - p) who say that they will vote Republican. If this poll is taken many
times for different samples one will find that the distribution of the results
for x (which is the number of people who say they will vote Democratic)
follows a binomial distribution with the mean of x =
= N(1 - p) who say that they will vote Republican. If this poll is taken many
times for different samples one will find that the distribution of the results
for x (which is the number of people who say they will vote Democratic)
follows a binomial distribution with the mean of x =
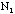 =
=
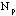 .
The probability distribution B(x) for finding x in a sample of N
is a function of the probabilities p and q, and is given by the
binomial distribution as follows:
.
The probability distribution B(x) for finding x in a sample of N
is a function of the probabilities p and q, and is given by the
binomial distribution as follows:
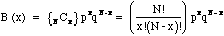 (1.1)
(1.1)
where x = 0,1,2,...,N and N! = N(N-1)(N-2)...1. 0! =1 by definition. Here
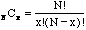 is the number of combinations for x objects taken from a sample of
N, px is the probability of getting x number of Democratic voters, and
qN-x is the probability of having the remain N-x voters be Republican. The
above equation acts as a model that can provide the probability of having a
particular x value. Often, the most needed information provided by this
distribution is the mean of x and its standard deviation,
is the number of combinations for x objects taken from a sample of
N, px is the probability of getting x number of Democratic voters, and
qN-x is the probability of having the remain N-x voters be Republican. The
above equation acts as a model that can provide the probability of having a
particular x value. Often, the most needed information provided by this
distribution is the mean of x and its standard deviation,
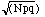 .
(1.2)
.
(1.2)
For example, if p = 0.51 and q = 0.49 and N = 900, one
expects that the poll will indicate a number close to 50% for the fraction who
say that they will vote Democratic. The pollster will find a number x
close to Np = 900x0.51 (i.e. around 459) with a standard deviation expected to
be
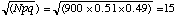 .
.
If in a particular poll the pollster finds x = 450, he will claim that the poll
indicates that 50% (450/900) will vote Democratic with a margin of error of
1.7% (15/900) (another way to calculate the margin of error is given in an
optional section at the end of this section). It is not likely that the
pollster will find a number such as 40%. This is because 900x0.4 = 360, which
is 99 away from the expected number of 459. It is possible but very unlikely
that the results will be six (99/15) standard deviations away from the expected
value.
For large N and small p, the binomial distribution approaches a
Poisson distribution. The Poisson distribution is more commonly applied
to phenomenon which occur at a random fixed rate. For example, suppose you
stand outside and count the number of people walking by. You stand for 1 hour
and count n = 900. If you repeated the experiment many times, you would
find the mean of the number of people passing by in one hour is M. The
standard deviation of the Poisson distribution is given by,
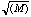 .
(1.3)
.
(1.3)
The Poisson distribution for measuring n = x when the expected mean is M
is given by,
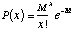 .
(1.4)
.
(1.4)
where e = 2.71828, and x = 1, 2, 3.... Note that the mean M, does not
need to be an integer.
For large values of N (the total number for the case of the binomial
distribution), and also for large values of M for the case of the
Poisson distribution (say M greater than 10 - 30) both binomial and the Poisson
distributions approach a Gaussian (normal or Bell curve) distribution.
The normal distribution has a mean M and a standard deviation
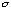 ,
which are independent. It is a continuous probability distribution G(x) given
by,
,
which are independent. It is a continuous probability distribution G(x) given
by,
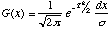 , (1.6)
, (1.6)
where
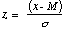
If you take the point in the normal distribution that is one standard deviation
below the mean and the point that is one standard deviation above the mean, the
area under the curve between the two points is 0.6827, or 68.27%. That is, the
probability of a single measurement falling within one standard deviation of
the mean is 68.27%. The probabilities of it to fall between +/-2 and +/-3
standard deviations are 0.9545 and 0.9973, respectively. To the extent that
the binomial and Poisson distributions can be approximated by a normal
distribution, these probabilities are indicative of how likely or unlikely for
a measurement to fall outside one, two or three standard deviations of the
mean.
Distribution Mean Standard Deviation
-------------------------------------------------------------
binomial Np 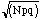 Poisson M
Poisson M 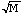 normal(Gaussian) M
normal(Gaussian) M 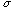 -------------------------------------------------------------
-------------------------------------------------------------
Table 1.1
Prelab Homework
Before you do this prelab, read this lab, and the file on Error
Analysis. The prelab homework must be done at home and handed to the lab
TA before you start the lab.
In order to do this prelab you need to understand the concept of a
standard deviation for a binomial distribution.
Questions
It is the month of August and a group of students are having dinner. They are
discussing a recent Campus Times article on a medical study which reported that
1 in 10 of the general population suffers from allergies to ragweed pollen.
Two of the students were sneezing and rubbing their eyes during the dinner.
They lamented the fact that this was ragweed season and they were really
suffering.
- One student noticed that sitting around the table, there were 2
students who were allergic to ragweed and 8 students who were not. He commented
that it was a ratio of 2/10 = 0.20, in contrast to the medical study claiming
that the ratio should be 1/10= 0.10. He said that this indicated that
students at the U of R were twice as likely to be allergic to ragweed than the
national average.
- What is the standard deviation expected from the binomial
distribution and the sample size of ten students?
- How many standard deviations away from the national average are the
results of this experiment?
- Are the results of this experiment consistent with the national
average?
- The rumor quickly spread around campus, and people began to worry
about the allergy cluster in Lattimore Hall. Some people commented that
exposure to chemicals can increase the likelihood of developing allergies, and
that those people were most likely chemistry majors. Not having access to the
original source of the rumor, some students decided to conduct their own
independent studies. Student A stood for one hour outside Wilson Commons and
asked students if they were allergic to ragweed. After one hour he found that
61 students did not have allergies and 3 students did. He calculated that the
ratio of the two groups was 3/64 = 0.047, and concluded that at the U of R the
ragweed allergy rate was actually half of the national average.
Are the results of this experiment consistent with the national average? Can
you offer a likely explanation for the result? Be quantitative, use
the concept of standard deviation.
- Two other students decided to do a more elaborate study. Student C
stood outside Wilson Commons for a full day and student D did a similar survey
in Marketplace Mall. Student C found that there were 40 students with this
allergy and 605 students without and obtained a ratio 40/645 = 0.062. Student
D's sample consisted of 702 people with no allergy and 81 people with allergy
to ragweed for a ratio of 81/783 = 0.103.
What conclusion should student C and student D conclude from their joint
venture? Can you offer some likely explanation for their results? Be
quantitative; use the concept of standard deviation.
- A comment by a student on one of the 1992 student TA evaluation
questionnaires: "Why do we have to learn about errors? The physics department
should just buy good and accurate equipment." What can you say about this
student's comment?
The Experiment
You will need to bring to this lab:
- A scientific calculator.
- Linear graph paper
- A completed error analysis pre-lab assignment
Procedure
The experiment consists of measuring the fraction of galvanized
(silver or nickel color) washers in a mixture of both galvanized and non
galvanized (yellow brass color) 1/4-20 brass washers. The 10"x17" plastic
bucket contains 24 lb (about 4500) of yellow brass washers, and 8 lb (about
1500) of galvanized (silver color) washers. The washers have been mixed, so
the probability of getting a galvanized washer is about 1500/6000 = 0.25. The
TA should give each student a small 6" metal bucket containing a random sample
of 100 washers from the mixed large bucket (obtained by weight). The TA should
do the experiment as one of the students.
Check List
Each student (including the TA) is given:
- A 6" metal bucket containing 0.5 lb. of washers. The bucket should
contain 100 washers.
- A 3" clear plastic cup containing total of 11 plastic washers to be
used as spacers.
- A 9" long aluminum rod which is threaded at both ends.
- Two 1/4-20 wings nuts.
A. Setting up the Data Sample:
- Remove one of the nuts from the end of the aluminum rod. Place one
plastic washer on the rod.
- Mix the 100 washers in your metal bucket.
- Without looking directly at the cup, take one metal washer at a time
and put it on the rod. When you have counted 10 metal washers, place a plastic
washer on the rod as a spacer.
- Repeat until you have ten groups of 10 metal washers spaced by
plastic washers. This consists of your data sample. If you have extra metal
washers left over, return them to the TA. If you do not have enough, ask the TA
for more.
B. Obtaining Data for a Binomial Distribution with n=10:
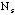 =
number of students in the lab =
=
number of students in the lab =
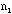 =
number of silver washers in a group of 10 =
=
number of silver washers in a group of 10 =
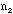 =
number of brass washers in a group of 10 =
=
number of brass washers in a group of 10 =
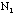 =
total number of silver washers you have =
=
total number of silver washers you have =
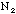 =
total number of brass washers you have =
=
total number of brass washers you have =
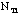 =
total number of silver washers in class =
=
total number of silver washers in class =
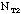 =
total number of brass washers you have =
=
total number of brass washers you have =
- N = 100 = total number of washers you have
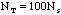 =
total number of washers in class =
=
total number of washers in class =
- p = fraction of any sample that is silver =
- q = 1 - p = fraction of any sample that is brass =
- Check your rod and record the number of combinations that you see on
the rod. Silver-color/yellow color: (
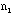 /
/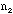 ,
with
,
with
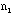 +
+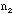 = 10).
= 10).
Individual Totals:
0/10 1/9 2/8 3/7 4/6 5/5 6/4 7/3 8/2 9/1 10/0 Total
Record the # of combinations under each combination above. You should have a
total of 10 samples. You should give this data to the TA.
- Total number of students (about 20) in the class (including the TA):
Ns =
- The TA should ask each student how many
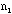 /
/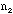 combinations she or he has and add up the total number of combinations
combinations she or he has and add up the total number of combinations
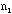 /
/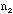 for all the students in the class for a total of 10xNs(about 200) samples.
for all the students in the class for a total of 10xNs(about 200) samples.
- Record the data for each student in the data sheet at the end of this
lab.
- Copy the totals for the 10xNs samples in the class silver/yellow : (
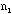 /
/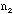 ,
with
,
with
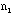 +
+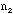 = 10).
= 10).
Class Totals
0/10 1/9 2/8 3/7 4/6 5/5 6/4 7/3 8/2 9/1 10/0 Total
- Record # of combinations(under each combination above). You should
have a total of about 200 (= 10x Ns) samples.
C. Obtaining Data for a Binomial Distribution with n=100:
Data Analysis
The following data analysis is to be done in the lab after the experiment is
completed. You need the data from the other students in order to complete the
analysis. The lab report is to be handed in within one week. The entire
laboratory is expected to take one hour, with one additional hour for the data
analysis.
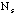 =
number of students in the lab =
=
number of students in the lab =
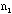 =
number of silver washers in a group of 10 =
=
number of silver washers in a group of 10 =
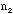 =
number of brass washers in a group of 10 =
=
number of brass washers in a group of 10 =
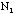 =
total number of silver washers you have =
=
total number of silver washers you have =
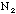 =
total number of brass washers you have =
=
total number of brass washers you have =
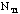 =
total number of silver washers in class =
=
total number of silver washers in class =
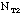 =
total number of brass washers in class =
=
total number of brass washers in class =
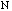 =100:
total number of washers you have
=100:
total number of washers you have
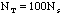 :
total number of washers in class
:
total number of washers in class
- p = fraction of any sample that is silver
- q = 1 - p = fraction of any sample that is brass
- Determine p = (#silver/total) and q = (#yellow/total)
for the sample taken by the entire class (as done below). Determine the
uncertainty (standard deviation) in p and q:
Using the entire class sample:
Mean values for p and q:
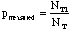 and
and
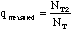
Expected error in p = expected error in q =
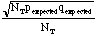
Required input / calculation:
- Total number of silver washers in class sample =
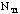 = _________
= _________
- Total number of yellow washers in class sample
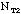 = _________
= _________
- Total number of washers in the class sample (
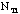 +
+ 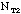 )
=
)
=
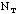 =
_________
=
_________
(Should be 100xNs or about 2000)
- p (measured) =______
- q(measured) = ______
- The expected standard deviation for
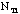 given p=0.25 and q =0.75 should be
given p=0.25 and q =0.75 should be
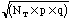 .
Use this expression to obtain the error in p(measured) and q(measured):
.
Use this expression to obtain the error in p(measured) and q(measured):
Expected error in p =______
Expected error in q =______
- How many standard deviations is p away from expectation?
Using your own sample of 100 washers:
Mean values for p and q:
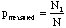 and
and
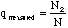
Expected error in p = expected error in q =
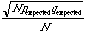
Required input / calculation:
- Tests of the binomial distribution with N=100.
- Make a table and then plot the distribution of
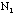 silver using the Ns samples of the class.
silver using the Ns samples of the class.
Mean of
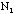 :
:
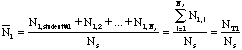
standard deviation of
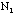 :
:
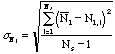
- Find the mean of
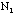 ,
and the standard deviation of the distribution for the data taken by the
class. For the calculation of standard deviation of the sample use the formula
from the file on Error Analysis. Note that if there are 20 students
there should be 20 samples of
,
and the standard deviation of the distribution for the data taken by the
class. For the calculation of standard deviation of the sample use the formula
from the file on Error Analysis. Note that if there are 20 students
there should be 20 samples of
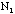 .
.
Is the standard deviation consistent with the expected standard deviation?
A better estimate of the expected standard deviation from a set of 20
measurements is given by the standard deviation of the sample times
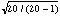 (see file on Error Analysis).
(see file on Error Analysis).
Let u=x+
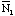 -25
-25
Let v=
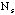 y
y
Then plot u vs. v
- For the distribution of
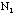 (mean should be around
(mean should be around
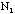 =25)
the normal distribution should be a good approximation to the Poisson and
binomial distributions. Plot a normal distribution with a mean equal to the
data, but with a standard deviation of 5. Use the attached table of the values
of the normal distribution for mean = 25, and standard deviation of 5. Shift
the x position of the plotted curve such that it agrees with the mean
for the data. The attached table is a probability distribution which is
normalized to 1.0. Therefore, the y values need to be multiplied by Ns
in order to normalize the distribution to the total number of samples.
=25)
the normal distribution should be a good approximation to the Poisson and
binomial distributions. Plot a normal distribution with a mean equal to the
data, but with a standard deviation of 5. Use the attached table of the values
of the normal distribution for mean = 25, and standard deviation of 5. Shift
the x position of the plotted curve such that it agrees with the mean
for the data. The attached table is a probability distribution which is
normalized to 1.0. Therefore, the y values need to be multiplied by Ns
in order to normalize the distribution to the total number of samples.
- Tests of the binomial distribution with N=10 (using 10xNs
samples).
- Repeat the same analysis as the previous example 14(a) but now do it
for the distribution of
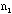 (mean should be about 2.5), using the 10xNs samples of ten washers each.
(mean should be about 2.5), using the 10xNs samples of ten washers each.
Mean of
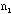 :
:
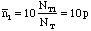
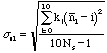 ,
where
,
where
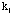 is the number of groups of ten washers in the class having i silver
washers in them.
is the number of groups of ten washers in the class having i silver
washers in them.
- The attached tables gives the binomial distribution for N=10, p =
0.25 and q = 0.75. They also give the Poisson distribution for M = 2.5, and the
Gaussian distribution with mean = 2.5 and standard deviation =
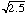 Plot the binomial, Poisson and Gaussian distributions with a mean of 2.5 and
compare to the data.
Plot the binomial, Poisson and Gaussian distributions with a mean of 2.5 and
compare to the data.
Note that the probability distributions must be multiplied by the number in the
sample (about 200). In order to get an idea of how well the distribution fits
the data, you must plot the data with error bars. For the measured
distribution, the error in each point on the distribution can be obtained by
assuming that the error on k is
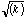 where k is the number of samples with that value of
where k is the number of samples with that value of
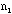 .
This makes the assumption that counting experiments are Poisson distributed and
have a typical error of
.
This makes the assumption that counting experiments are Poisson distributed and
have a typical error of
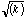 .
.
Multiply y values of the binomial, Poisson, and Gaussian data by
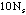 and plot on the graph of experimental points (
and plot on the graph of experimental points (
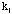 vs. i)
vs. i)
- Have your plots and data sheet signed by the TA. These
should be handed in as part of your lab report.
Lab Homework (Due one week after the lab)
Finish a complete lab report for this experiment. Follow the
example given in the file Writing a Lab Report. In addition, hand in the
following Lab homework :
- Read the file on Error Analysis and learn to do combination
of errors either by differentiation or by using the error table at the end of
the file. Learn the difference between statistical and systematic errors.
- For g=[2s/t2 ] what is the contribution to the error in
g (
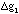 )
from an error in s ([[Delta]]s), and what is the contribution to
the error in g (
)
from an error in s ([[Delta]]s), and what is the contribution to
the error in g (
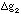 )
from an error in t ([[Delta]]t). What is the total error in
g ([[Delta]]g total)?
)
from an error in t ([[Delta]]t). What is the total error in
g ([[Delta]]g total)?
- The error [[Delta]]t in a single measurement of time for
a falling body is 2 seconds. Four measurements of the time are performed and
averaged. What is the error of the mean, the average of the four times?
(a) If [[Delta]]t is a random error. (b) If [[Delta]]t is a systematic (e.g.
scale) error. (Hint: You should get real values (in seconds) and (a) is less
than (b).)
- Optional
There is another way of calculating margin of error for the presidential
poll result described in the beginning of this lab. We chose the case in which
the total number of people sampled is 900, and there is a probability of p =
0.5 of voting Democratic and q = 0.5 of voting Republican.
If the sampling number N, (or 900 in our example), is not fixed, but is chosen
randomly, then one can say that
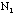 and
and
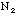 are independent variables and are randomly distributed. Therefore,
are independent variables and are randomly distributed. Therefore,
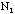 and
and
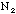 are two independent measurements and each is Poisson distributed with
standard errors
are two independent measurements and each is Poisson distributed with
standard errors
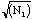 and
and
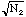 ,
respectively. The fraction of people voting Democratic is
,
respectively. The fraction of people voting Democratic is
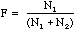 .
.
By taking the derivative of F with respect to
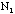 and with respect to
and with respect to
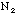 and by adding the errors in F from
and by adding the errors in F from
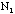 and
and
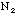 in quadrature (i.e., using the standard rules for the addition of independent
errors), one finds that the standard error in F is equal to
in quadrature (i.e., using the standard rules for the addition of independent
errors), one finds that the standard error in F is equal to
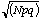 .
The details are left as an exercise for the student.
.
The details are left as an exercise for the student.
References
1. Schaum's outline series, "Statistics" by Murray R. Spiegel, McGraw
Hill Book Company.
2. Data and Error analysis in the introductory "Physics Laboratory", by
William Lichten, Allyn and Bacon Inc. Newton, MA. 1988.
3. See also references in file: Error Analysis.
DATA SHEET FOR RECORDING CLASS SAMPLE
(record number of combinations for each student in the class)
Combination: (Silver-Color/Yellow-Color)
0/10, 1/9, 2/8, 3/7, 4/6, 5/5, 6/4, 7/3, 8/2, 9/1, 10/0,(?=10) Silver
Student 1: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 2: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 3: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 4: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 5: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 6: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 7: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 8: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 9: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 10: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 11: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 12: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 13: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 14: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 15: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 16: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 17: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 18: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 19: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 20: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 21: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 22: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 23: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 24: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 25: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
Student 26: ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
TOTAL : ____, ____, ____, ____, ____, ____, ____, ____, ____, ____, ____:____,: ____
* Check that the sum total is 10xNs, where Ns is the number of
students.
* Copy the results of the Total to Section B.
Examples of various distribution with a mean of 2.5
Binomial Distribution:

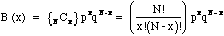
where
N=10
p=0.25
q=0.75
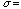
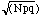
Poisson Distribution:
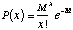
where
M=2.5
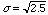
Gaussian Distribution:
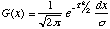
where
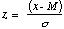
M=2.5
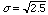
Binomial, Poisson, and Gaussian Distributions with
mean=2.5
Data Points
x binomial Poisson Gaussian
0 0.056314 0.082085 0.072289
1 0.187712 0.205212 0.160882
2 0.281568 0.256516 0.240008
3 0.250282 0.213763 0.240008
4 0.145998 0.133602 0.160882
5 0.058399 0.066801 0.072289
6 0.016222 0.027834 0.021773
7 0.003090 0.009941 0.004396
8 0.000386 0.003106 0.000595
9 0.000029 0.000863 0.000054
10 0.000001 0.000216 0.000003
Gaussian Distribution(mean=25, dx=
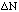 =1,
=1,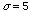 )
)
x y x y
0 0.000000 26 0.078209
1 0.000001 27 0.073654
2 0.000002 28 0.066645
3 0.000005 29 0.057938
4 0.000012 30 0.048394
5 0.000027 31 0.038837
6 0.000058 32 0.029945
7 0.000122 33 0.022184
8 0.000246 34 0.015790
9 0.000477 35 0.010798
10 0.000886 36 0.007095
11 0.001583 37 0.004479
12 0.002717 38 0.002717
13 0.004479 39 0.001583
14 0.007095 40 0.000886
15 0.010798 41 0.000477
16 0.015790 42 0.000246
17 0.022184 43 0.000122
18 0.029945 44 0.000058
19 0.038837 45 0.000027
20 0.048394 46 0.000012
21 0.057938 47 0.000005
22 0.066645 48 0.000002
23 0.073654 49 0.000001
24 0.078209 50 0.000000
25 0.079788
Send comments, questions and/or suggestions via email to wolfs@nsrl.rochester.edu.
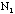 =
=
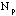 people who say that they will vote Democratic, and
people who say that they will vote Democratic, and
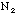 =
=
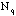 = N(1 - p) who say that they will vote Republican. If this poll is taken many
times for different samples one will find that the distribution of the results
for x (which is the number of people who say they will vote Democratic)
follows a binomial distribution with the mean of x =
= N(1 - p) who say that they will vote Republican. If this poll is taken many
times for different samples one will find that the distribution of the results
for x (which is the number of people who say they will vote Democratic)
follows a binomial distribution with the mean of x =
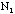 =
=
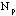 .
The probability distribution B(x) for finding x in a sample of N
is a function of the probabilities p and q, and is given by the
binomial distribution as follows:
.
The probability distribution B(x) for finding x in a sample of N
is a function of the probabilities p and q, and is given by the
binomial distribution as follows: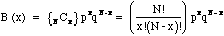 (1.1)
(1.1)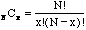 is the number of combinations for x objects taken from a sample of
N, px is the probability of getting x number of Democratic voters, and
qN-x is the probability of having the remain N-x voters be Republican. The
above equation acts as a model that can provide the probability of having a
particular x value. Often, the most needed information provided by this
distribution is the mean of x and its standard deviation,
is the number of combinations for x objects taken from a sample of
N, px is the probability of getting x number of Democratic voters, and
qN-x is the probability of having the remain N-x voters be Republican. The
above equation acts as a model that can provide the probability of having a
particular x value. Often, the most needed information provided by this
distribution is the mean of x and its standard deviation,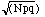 .
(1.2)
.
(1.2) 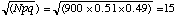 .
.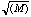 .
(1.3)
.
(1.3)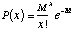 .
(1.4)
.
(1.4)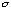 ,
which are independent. It is a continuous probability distribution G(x) given
by,
,
which are independent. It is a continuous probability distribution G(x) given
by,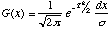 , (1.6)
, (1.6) 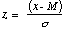
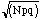 Poisson M
Poisson M 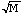 normal(Gaussian) M
normal(Gaussian) M 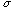 -------------------------------------------------------------
-------------------------------------------------------------
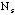 =
number of students in the lab =
=
number of students in the lab = 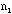 =
number of silver washers in a group of 10 =
=
number of silver washers in a group of 10 = 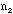 =
number of brass washers in a group of 10 =
=
number of brass washers in a group of 10 = 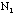 =
total number of silver washers you have =
=
total number of silver washers you have = 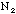 =
total number of brass washers you have =
=
total number of brass washers you have = 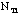 =
total number of silver washers in class =
=
total number of silver washers in class = 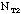 =
total number of brass washers you have =
=
total number of brass washers you have = 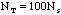 =
total number of washers in class =
=
total number of washers in class =
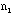 /
/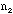 ,
with
,
with
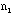 +
+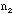 = 10).
= 10).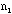 /
/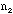 combinations she or he has and add up the total number of combinations
combinations she or he has and add up the total number of combinations
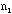 /
/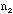 for all the students in the class for a total of 10xNs(about 200) samples.
for all the students in the class for a total of 10xNs(about 200) samples. 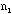 /
/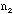 ,
with
,
with
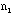 +
+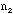 = 10).
= 10).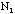 = _______.
= _______.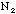 = _______.
= _______.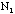 /
/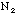 (with
(with
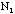 +
+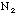 = 100) values for each person.
= 100) values for each person. 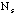 =
number of students in the lab =
=
number of students in the lab = 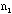 =
number of silver washers in a group of 10 =
=
number of silver washers in a group of 10 =
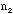 =
number of brass washers in a group of 10 =
=
number of brass washers in a group of 10 =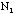 =
total number of silver washers you have =
=
total number of silver washers you have =
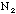 =
total number of brass washers you have =
=
total number of brass washers you have =
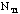 =
total number of silver washers in class =
=
total number of silver washers in class =
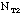 =
total number of brass washers in class =
=
total number of brass washers in class = 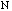 =100:
total number of washers you have
=100:
total number of washers you have
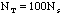 :
total number of washers in class
:
total number of washers in class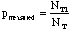 and
and
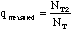
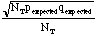
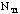 = _________
= _________ 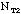 = _________
= _________ 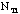 +
+ 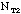 )
=
)
=
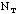 =
_________
=
_________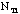 given p=0.25 and q =0.75 should be
given p=0.25 and q =0.75 should be
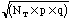 .
Use this expression to obtain the error in p(measured) and q(measured):
.
Use this expression to obtain the error in p(measured) and q(measured):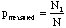 and
and
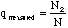
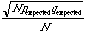
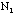 and
and
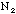 ).
).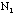 = _________
= _________ 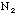 = _________
= _________ 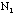 +
+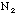 )
= N =__________
)
= N =__________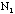 given p=0.25 and q =0.75 should be
given p=0.25 and q =0.75 should be
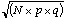 .
Use this expression to obtain the error in p(measured) and q(measured):
.
Use this expression to obtain the error in p(measured) and q(measured):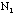 silver using the Ns samples of the class.
silver using the Ns samples of the class. 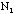 :
:
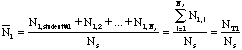
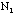 :
:
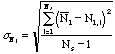
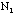 ,
and the standard deviation of the distribution for the data taken by the
class. For the calculation of standard deviation of the sample use the formula
from the file on Error Analysis. Note that if there are 20 students
there should be 20 samples of
,
and the standard deviation of the distribution for the data taken by the
class. For the calculation of standard deviation of the sample use the formula
from the file on Error Analysis. Note that if there are 20 students
there should be 20 samples of
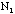 .
.
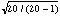 (see file on Error Analysis).
(see file on Error Analysis).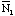 -25
-25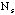 y
y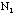 (mean should be around
(mean should be around
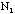 =25)
the normal distribution should be a good approximation to the Poisson and
binomial distributions. Plot a normal distribution with a mean equal to the
data, but with a standard deviation of 5. Use the attached table of the values
of the normal distribution for mean = 25, and standard deviation of 5. Shift
the x position of the plotted curve such that it agrees with the mean
for the data. The attached table is a probability distribution which is
normalized to 1.0. Therefore, the y values need to be multiplied by Ns
in order to normalize the distribution to the total number of samples.
=25)
the normal distribution should be a good approximation to the Poisson and
binomial distributions. Plot a normal distribution with a mean equal to the
data, but with a standard deviation of 5. Use the attached table of the values
of the normal distribution for mean = 25, and standard deviation of 5. Shift
the x position of the plotted curve such that it agrees with the mean
for the data. The attached table is a probability distribution which is
normalized to 1.0. Therefore, the y values need to be multiplied by Ns
in order to normalize the distribution to the total number of samples.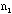 (mean should be about 2.5), using the 10xNs samples of ten washers each.
(mean should be about 2.5), using the 10xNs samples of ten washers each.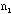 :
:
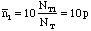
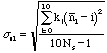 ,
where
,
where
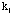 is the number of groups of ten washers in the class having i silver
washers in them.
is the number of groups of ten washers in the class having i silver
washers in them.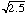 Plot the binomial, Poisson and Gaussian distributions with a mean of 2.5 and
compare to the data.
Plot the binomial, Poisson and Gaussian distributions with a mean of 2.5 and
compare to the data.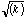 where k is the number of samples with that value of
where k is the number of samples with that value of
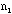 .
This makes the assumption that counting experiments are Poisson distributed and
have a typical error of
.
This makes the assumption that counting experiments are Poisson distributed and
have a typical error of
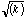 .
.
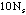 and plot on the graph of experimental points (
and plot on the graph of experimental points (
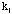 vs. i)
vs. i)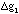 )
from an error in s ([[Delta]]s), and what is the contribution to
the error in g (
)
from an error in s ([[Delta]]s), and what is the contribution to
the error in g (
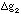 )
from an error in t ([[Delta]]t). What is the total error in
g ([[Delta]]g total)?
)
from an error in t ([[Delta]]t). What is the total error in
g ([[Delta]]g total)?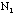 and
and
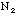 are independent variables and are randomly distributed. Therefore,
are independent variables and are randomly distributed. Therefore,
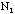 and
and
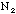 are two independent measurements and each is Poisson distributed with
standard errors
are two independent measurements and each is Poisson distributed with
standard errors
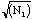 and
and
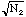 ,
respectively. The fraction of people voting Democratic is
,
respectively. The fraction of people voting Democratic is
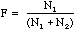 .
.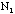 and with respect to
and with respect to
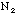 and by adding the errors in F from
and by adding the errors in F from
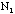 and
and
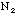 in quadrature (i.e., using the standard rules for the addition of independent
errors), one finds that the standard error in F is equal to
in quadrature (i.e., using the standard rules for the addition of independent
errors), one finds that the standard error in F is equal to
 .
The details are left as an exercise for the student.
.
The details are left as an exercise for the student.
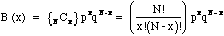
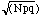
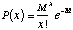
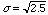
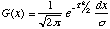
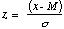
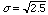
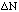 =1,
=1,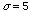 )
)