(2.1)NOTE
This manual describes the laboratory experiment used during the 1996 - 1997 academic year. Significant changes have been made since then, and the manual used during the current academic year is in NOT available yet on the WEB. Hardcopies can be purchased at the bookstore.
The purpose of this lab is to measure the constant acceleration g due to gravity near the earth's surface by two different methods. The value of g at the University of Rochester is 9.8039 m/s2. You will do this by performing two different experiments:
1. Experiment 2A - Freely Falling Body (room B267)
2. Experiment 2B - The Atwood Machine (room B266)
The acceleration of an object due to the earth's gravitation is,
(2.1)
where G is Newton's gravitational constant, 
is the mass of the earth and r is the distance to the center of
the earth. Inasmuch as the radius of the earth is very large compared
to laboratory dimensions, an object near the surface of the earth,
r is approximately constant and equal to the radius of the earth,
. Thus an object near the surface of the
earth will experience a nearly constant acceleration,
(2.2)
(There are instruments which are sensitive enough to measure the difference in g due to the difference in Re of a few meteres. The experiments that you are going to do in this laboratory, needless to say, are not that sensitive).
You will consider the effects of constant acceleration g . It is useful to recall the result due to any constant acceleration a . If the body, initially at rest, is subject to a constant acceleration a , then its subsequent displacement s, is given by,
(2.3)
where t is the length of time over which the acceleration has been acting. By measuring the displacement as a function of time elapsed after starting from rest, the acceleration can be determined.
In Experiment 2A, Freely Falling Body, the acceleration a is g and is determined by measurement of s and t.. In Experiment 2B, The Atwood Machine, the acceleration of gravity is "slowed down" so that one measures a smaller acceleration a (presumably more accurate). This acceleration is related to g by the equation given below (2.4).
The prelab homework must be done at home and handed to the
lab TA before you start the lab.
1. a) Using the known values of the mass of the earth and the radius of the earth. Calculate the value of g.
b) What is the change in g( 
)
if the measuring apparatus is raised in height by 1 meter?
2. Derive equation 2.3 for the distance that a body moves under an acceleration a. .
3. For Atwood's machine, derive the formula,
(2.4)
where M1 and M2 are the two masses, a is the acceleration of the masses and g is the acceleration due to gravity.
While this may seem to be the most obvious method of measuring g, it was not practical until the advent of modern electronic timers. The acceleration of gravity is measured by allowing a steel ball to fall, after starting at rest, and then applying the equation for accelerated motion. A free fall timer is used in this experiment.
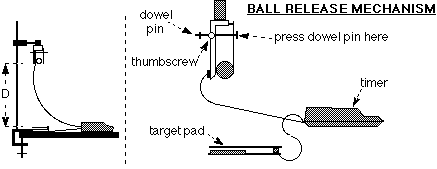
Figure 2.1
1. The ball release mechanism should be clamped to a stand.
2. Position the target pad directly under the ball release mechanism.
3. Place the timer so that it will not be hit by a falling ball.
4. Now make a test run by clamping a ball into the release mechanism. Close the release mechanism by pushing on the dowel pin as shown, and then tightening the thumbscrew to lock the ball in place. Turn the timer on and press reset. Finally, turn the thumbscrew counter-clockwise to release the ball which should then drop on the middle of the target pad. The ball falls a distance measured from the bottom of the ball to the top of the plate.
5. Remember to hit reset between each measurement.
For five different arbitrary distances (measured from the bottom of the ball in the ball release to the top of the pad) measure five free fall times. Measure the distance each time also(i.e. you make pairs of measurements of t and h.).
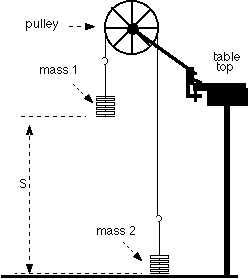
Figure 2.2
Atwood's machine is shown in the diagram Figure 2.2. The arrangement of the weights minimizes the effects of random errors so this is a fairly accurate method for measuring g. Since this experiment can be done without the use of electronic timers, it was one of the original ways to measure g accurately. (Had accurate timers been available it is doubtful that this method would have found favor. So, this method is mainly of historic interest).
Ideally, the pulley would be firmly supported and frictionless. The cord connecting the two masses would be unstretchable and massless. To the extent that the cord does not stretch, the motion of the system is determined by the motion of either weight alone.(i.e. The length of the cord is constant.) The acceleration due to gravity can be found from the formula,
(2.5)
where M1 and M2 are the masses
, and a is the acceleration of the masses.
Because g is constant, we see that a must be constant. The formula,
,
can be applied to find a, and thus we can calculate g.
The experiment works best when the sum of the masses is large when compared to the difference between the masses. As is shown in the diagram, start off with the heavier mass (labeled M1) above the lighter mass. Practice letting M1 fall a few times before starting to take real measurements.
1) For one combination of M1 and M2,
use a meterstick and a stopwatch to make four measurements
of the time it takes for a weight starting at rest to traverse
a distance s( again measure s everytime you measure t ), Keep
in mind that the difference in masses should be kept small (no
more than 80g) while keeping the sum of the two masses large (400g
to 500g). It is best if the same person who starts and stops the
timer also drops the mass. The other person should measure the
distance. You should have a table of t and s pairs. Also record
and 
.
2) Now change 
and
and repeat the above procedure three
more times, giving you a total of four sets of measurements.
Keep the sum of the two masses constant, while changing
the difference between the two masses by moving weights from one
to the other.
1) Calculate the average time 
and
the uncertainty 
(i.e. the
standard deviation of t ). Also calculate 
and s . Do this for each sample of five measurements.
2) Plot 
including error bars,
, (i.e. the standard deviation) on the y-axis
versus the square of 
including the
error bars on the x-axis. (How is the standard deviation of the
square oft related to the standard deviation of t , (See Appendix,
Error Analysis). Using a ruler, find and draw the "best"
straight line through the points. The slope is g/2.
3) Now calculate g from the data for each of the four distances and find average g +/- [Delta]g. Compare this average and error to the value from the slope and to the accepted value of g.
1) By how many standard deviations do your answers differ from the accepted value?
2) Does the plot intercept the origin, and if not, what are possible explanations for this?
1) For each of the four sets (i.e. different 
,
) compute 
,
and 
, 
.
2) From the data compute 
and 
for each of the four data sets. (See Appendix
on Propagation of Errors.)
3) Plot a vs. (M1 - M2)/(M1
+ M2). Show the uncertainty in a but you may
assume that there is no uncertainty in 
or 
. Fit a line through the points making sure
the fit line passes close to the error bars of all the points.
Although the line should pass through the origin, do not force
it to. The slope of the "best" line through these points
is g .
1) How does the value of g from the slope compare to the accepted value?
2) Are there any systematic errors to be considered(Hint: friction in pulley)?
3) Does your "best" straight line go through the origin? If not, what errors are indicated?