
NOTE
This manual describes the laboratory experiment used during the 1996 - 1997 academic year. Significant changes have been made since then, and the manual used during the current academic year is in NOT available yet on the WEB. Hardcopies can be purchased at the bookstore.
The purpose of this lab is to observe the conversion of energy from one form to another.
In experiment A you will measure the proportional relationship of mechanical energy to thermal energy, which is known as Joule's constant [4.184 J/cal (Joules per calorie)].
In experiment B you will, using a light bulb, convert electrical energy into heat from which you will determine Joule's constant again for this process. You will then repeat this experiment but now allowing some of the energy to escape in the form of light. From this experiment you will be able to calculate the efficiency of conversion of electrical energy to light.
In particular you will do:
* Experiment 5A- Mechanical Energy into Heat (room B267)
* Experiment 5B- Electrical Energy (room B266)
1. Conversion of Electrical Energy into Heat
2. Conversion of Electrical Energy into Heat and Light
One of the most fundamental principles of physics is the Conservation of Energy. According this principle, energy can not be created or destroyed but may be transformed from one form to another. An early application of this principle was to explain the conversion of work to heat by Joule. This was soon extended to other experiments such as the conversion of electrical energy to work, heat, or light. Einstein' s famous equation E=mc2 is a statement of this principle. So strong is this principle that Pauli in 1931 confidently predicted the existence of a massless particle, the neutrino, to explain certain experiments. Direct confirmation was not obtained until 1953!
This must be done prior to coming to laboratory and handed to the TA .
1. A 90Kg person jumps from a 49m tower into a tub of water at 20 degrees Centigrade and volume 3.0 cubic meters. Assuming all of the energy is converted into heat, what is the final temperature of the water?
2. A 25 watt light bulb is immersed in .012 cubic meters of water. Assume that 20% of this power is converted to light and that the rest is absorbed by the water. If the bulb is turned on for 23 minutes, what will be the rise in the temperature ofthe water?

In this experiment you will convert mechanical energy into heat. The mechanical energy will come from friction. The heat will be observed by measuring the increase in temperature of known masses of known specific heat
capacity.
The common experience with friction is direct evidence for a relation between mechanical and thermal energy. When two reasonably rough objects are rubbed together they tend to warm up. Consider, for example, two hands on a cold Rochester morning or two dry sticks in the care of a skillful Boy/Girl Scout.
Joule noticed this fact and conjectured that the mechanical
work W done in rubbing is directly proportional to the quantity
of heat ![]() produced,
produced,
![]() (5.1)
(5.1)
where J is Joule's constant of proportionality. Joule devised elegant experiments that confirmed this relationship. He also showed that W could be any form of energy, not just work against friction, provided it is all converted to heat.
In this experiment you will recreate one of Joule's experiments
involving friction. Mechanical work is the product of a force
times the distance through which it acts, but how can one measure
heat? Heat changes a body to which it is added; for instance,
its temperature may rise or there maybe a phase change (e.g.,
from solid to liquid or liquid to gas). As long as there is no
change of phase and the temperature changes are small, to a first
approximation, the change in heat ![]() of a body is directly proportional to the change in its temperature.
Furthermore, since a body can be (conceptually) broken up into
smaller ones and the change in heat of the whole is the sum of
the heat changes of the parts, a given temperature change should
require an amount of heat directly proportional to the mass. Therefore,
of a body is directly proportional to the change in its temperature.
Furthermore, since a body can be (conceptually) broken up into
smaller ones and the change in heat of the whole is the sum of
the heat changes of the parts, a given temperature change should
require an amount of heat directly proportional to the mass. Therefore,
![]() (5.2)
(5.2)
where m is the mass and Ti and Tf are the initial and final temperatures, respectively. The constant of proportionality C, called the specific heat relates the temperature change of a given body to the quantity of heat that produces it. It is a characteristic of the material of which the body is composed. This relationship (C independent of temperature) is an approximation that is good over small temperature ranges.
The C.G.S. unit of heat, called the calorie, is defined as the quantity of heat required to raise one gram of water from a temperature of 14.5deg.C to 15.5deg.C. Hence, by definition, water has a specific heat of 1 cal/gm deg.C at that temperature. The specific heats of other materials are determined by comparison with water and are tabulated for many common materials. For instance, the tabulated value of the specific heat of brass is
![]() (5.3)
(5.3)
which you will need in analyzing your experiment.
This experiment consists of a moving part which rotates against a stationary brass mass (containing a thermometer). These two parts exert frictional forces on each other which generate heat. The stationary mass is constrained from rotating only by a measured force F applied at a radius r from its center. This situation is shown in a schematic way in Figure 5.1.
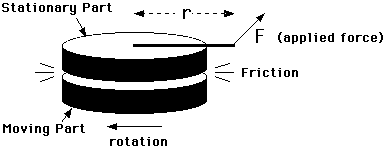
Figure 5.1
The moving part is rotated at a rate so that the frictional force transmitted to the stationary part just balances a constant torque applied to it and keeps it from moving. Under these conditions, all the work done to keep the moving part rotating is converted to heat by friction.
What is the rate at which mechanical energy is converted into
heat? Well, it does not matter which part moves and which is stationary
(except for the convenience of doing the experiment); the relative
motion is what produces the friction that balances the applied
torque. So, imagine that the moving part was stopped. The same
balance would occur when the stationary part rotates under the
influence of the applied torque such that the relative motion
is the same as before; that is, at the same rate that the moving
part was turning. The rate at which work would be done by the
applied force in this hypothetical situation is F s, where s is
the linear displacement parallel to the direction of the force.
In N revolutions the force effectively acts over a distance s
= ![]() , so that the work done, which is the rate
at which mechanical energy is converted into heat in both situations
is,
, so that the work done, which is the rate
at which mechanical energy is converted into heat in both situations
is,
![]() (5.4)
(5.4)
Thus by measuring the applied force F and the radius of the
point of application r , you can determine the frictional work
done W by counting the number of revolutions N. When F is expressed
in Newtons and r in meters then W is in Joules. This heat is absorbed
by the friction producing assembly and raises its temperature.
By measuring the resulting change in temperature ![]() T
with the thermometer, the heat absorbed by each of the parts is
T
with the thermometer, the heat absorbed by each of the parts is
![]() (5.5)
(5.5)
where ![]() is the heat absorbed by the ith
part with mass mi and specific heat Ci,
can be accounted for.
is the heat absorbed by the ith
part with mass mi and specific heat Ci,
can be accounted for.
Now the thermometer itself consists of both mercury and glass, and these substances have different specific heats. However, by fortunate coincidence the product of density and specific heat is,
![]() (5.6)
(5.6)
and is nearly the same for both glass and mercury. So, for the thermometer,
![]() (5.7)
(5.7)
where Vt is the effective volume of the thermometer. Since glass is a poor conductor of heat and the mercury column is very fine, there will not be much heat conducted up the thermometer during the experiment. Consequently, Vt amounts to only that portion of the volume of the thermometer in direct thermal contact with the heat producing assembly.
The total heat absorbed can then be obtained by adding together the partial heats,
![]() (5.8)
(5.8)
To do this the parts must be weighed and their specific heats known and the effective thermometer volume must be measured. Then, from these results, Joule's constant, J = W / [Delta]Q, can be calculated to give the relationship between mechanical energy and heat.
With this experiment, the rubbing parts are a plastic disk squeezed between a pair of brass cores. Tension screws can be adjusted to vary the amount of friction. The plastic disk is turned by a hand crank. A spring scale is attached by a wire to a winding screw on the periphery of one of the cores. This wire rides in a groove on the diameter of this core, to which it applies a measured force. In use, the plastic disk should be cranked at a rate so that the frictional forces exactly counterbalance the torque applied by the spring and the cores remain stationary.
The tension screws should be adjusted until the frictional load is around 1kg (+/-0.5kg) at a rate of one or two rotations per second; adjust them carefully and do not over-tighten them. After making these adjustments you should let the assembly cool to room temperature equilibrium before you do the experiment. To determine N, you must keep count the number of revolutions as you crank.
The heat produced by friction is measured by determining the change in temperature of the brass core assembly. This temperature change at several time intervals (every 50 rotations or so) is measured with a thermometer inserted in the core; it rests horizontally on a thermometer holder on the apparatus. Smear a small amount of grease on the thermometer bulb to insure good thermal contact with the brass core. The accuracy will decrease if you exceed about 10deg.C above ambient because then too much heat will leak to the surrounding air and the plastic friction disk.
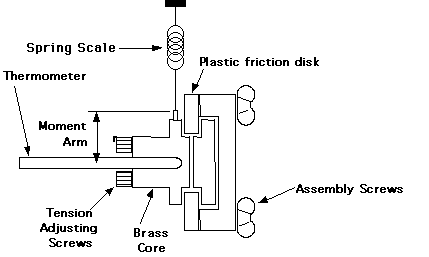
Figure 5.2. Mechanical Equivalent Apparatus
The items that are heated up consist of the brass core assembly
(both pieces of the core, the two tension screws and the wire
mounting screw) and the thermometer. The plastic disk has a very
low thermal conductivity so the heat it absorbs can be neglected.
Then the total heat generated ![]() is,
is,
![]() (5.9)
(5.9)
where
![]()
and the quantities
mc = mass of brass core assembly (in grams) and
Vt = volume of thermometer in core (in cm3)
must be measured after the experiment. Putting everything together yields,
![]() (5.10)
(5.10)
where [Delta]T is the change in temperature in N revolutions. You must also determine r the radius of core by measuring the diameter of the core with a pair of calipers.
Spend some time familiarizing yourself with your particular apparatus. You should practice coordinating between yourself and your lab partner the tasks of reading the thermometer at the right times, cranking at the proper speed, etc..
1. Before starting the experiment you must allow the apparatus to reach thermal equilibrium with the lab environment.
2. When ready, start the timer and start cranking the apparatus simultaneously. Remember that you should crank as steadily as possible and just vigorously enough to keep things stationary.
3. Take time and temperature readings and note the number of revolutions at about 30 sec. intervals but do not stop cranking.
4. Stop cranking when the temperature reaches about 8deg.C above the initial temperature. Record the final number of revolutions executed and note the time t when you do so.
5. Continue to take temperature readings at 30 sec intervals until your timer reads greater than 2t. This is done in order to adjust your data to include the effects of radiant cooling.
6. Measure the mass and dimensions of the brass. To do so, disassemble the apparatus by removing the assembly screws and the tension screws.
7. Estimate the inserted volume of the thermometer in the core by measuring the dimensions.
1. Plot all your data, temperature vs. time, on graph paper
and correct for radiant cooling as follows. Note that ![]() is
the maximum temperature at time t (not necessarily exactly at
the time that you stop doing work), and
is
the maximum temperature at time t (not necessarily exactly at
the time that you stop doing work), and ![]() is the temperature at time equals 2t. When plotting, draw two
"best" straight lines through the points for time <
t and for time between t and 2t. The intersection determines the
time t when the temperature is at its maximum value (T=
is the temperature at time equals 2t. When plotting, draw two
"best" straight lines through the points for time <
t and for time between t and 2t. The intersection determines the
time t when the temperature is at its maximum value (T= ![]() ).
See Figure 5.4.
).
See Figure 5.4.
The temperature change produced by doing work is apparently
![]() . But during the time t heat was being lost
to the environment by radiant cooling. An estimate of this heat
loss in time t is provided by the temperature drop
. But during the time t heat was being lost
to the environment by radiant cooling. An estimate of this heat
loss in time t is provided by the temperature drop ![]() .
Thus
.
Thus ![]() is not taken to be
is not taken to be ![]() but,
but,
![]() (5.11)
(5.11)
2. Calculate J, corrected for radiant cooling. If one estimates the error in J to be 1/2 of the correction to J which you made to J for radiant cooling then
![]() .
.
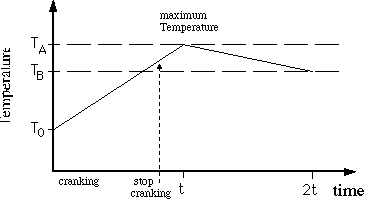
Figure 5.3
1. Is your answer compatible with J = 4.19 joules/cal, the accepted value?
2. Discuss other possible sources of error in the experiment and their relative importance (qualitative) in the final answer.
3. What are sources of the radiant cooling?
4. Why does the temperature rise from TB to TA without cranking
Another form of energy that we use in everyday is electrical. When a "light" switch is flipped on electricity flows through the filament of the lamp. The particles of electricity (electrons) collide with the nucleus of the lattice causing them to vibrate with larger amplitude (this is what we identifying with "heat"). Eventually the vibrated energy is radiated away as electromagnetic waves called photons (light particles). The spectrum consists of the infrared, the visible and the ultraviolet. This is the energy that escapes from the light bulb. Infrared is absorbed by the water causing the water temperature to increase. Visible light passes through water.
The amount of electrical energy ( E) consumed by the light
bulb is calculated by multiplying the power (P) used, by the amount
of time ( ![]() t) the light bulb is on. The power is found by
multiplying the voltage (V) with the electric current (I) going
through the light bulb[If V is in Volts, and I is in Amps, then
P is in Watts; the energy E will then be in Joules]. We then have
t) the light bulb is on. The power is found by
multiplying the voltage (V) with the electric current (I) going
through the light bulb[If V is in Volts, and I is in Amps, then
P is in Watts; the energy E will then be in Joules]. We then have
![]() (5.12)
(5.12)
If the light bulb is surrounded by material that will absorb almost all of the photons and whose specific heat is known, the total heat can be found again by using equation 5.8. (This is made with the assumption that a thermometer can be used with this material to measure its change in temperature.) Putting these together, the solution for the electrical equivalent of heat (Je) can be found:
![]() (5.13)
(5.13)
However if in a second experiment the material absorbs all the radiaton except the visible part of the spectrum, the efficiency of the lamp in producing light can be calculated from the following,
![]() (5.14)
(5.14)
The light bulb produces the energy, (5.12), and the water absorbs
the energy and is ![]() QJ. Here we now must
assume the value of J is known (4.184 J/cal).
QJ. Here we now must
assume the value of J is known (4.184 J/cal).
In the first experiment , we are assuming all energy produced by the light bulb is absorbed by the water when calculating Je. In particular a 35 Watt incandescent lamp is immersed in a known quantity of water and a few drops of India ink are added the water so it is opaque to visible light. The temperature of the water is measured. By monitoring the temperature of the water, the heat produced by the lamp can also be calculated. The ratio between the electrical energy that flows into the lamp and the heat energy produced by the lamp determines the electrical equivalent of heat.

Figure 5.4. Schematic of light bulb in EEH jar.
In a second experiment, the efficiency of the incandescent lamp is measured. The details are similar to the main part, but no India ink is added to the water. Without the ink, some of the energy from the lamp is absorbed into the water, where some visible light energy escapes. To determine the amount of energy that was released as light, the heat transferred into the water is subtracted from the total electrical energy that flowed into the lamp. The ratio between the light energy and the electrical energy gives the efficiency of the bulb.
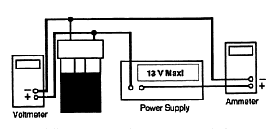
Figure 5.5
1. Measure and record the room temperature (Tr).
2. Weigh the EEH Jar assembly and the lid, and record its mass (Mj).
3. Remove the lid of the Jar and fill it to the indicated water. DO NOT OVERFILL (Filling beyond this level can significantly reduce the life of the lamp).
4. Add about 10 drops of India ink to the water; enough so the lamp filament is just barely visible when the lamp is illuminated.
5. Make sure electrical connections and setup corresponds to the following Figure 5.5.
6. Using leads with banana plug connectors, attach your power
supply to the terminals of the jar. Turn on the power supply and
quickly adjust the power supply voltage to about 8.5 volts, and
the ammeter should read about 4 amp, then shut the power off.
This is to allow the temperature of water come to an equilibrium.
DO NOT LET THE POWER EXCEED 35 WATTS! ![]() .
.
7. Insert the jar into one of the Styrofoam Calorimeters.
8. Insert your thermometer through the hole in the top of the jar. Stir the water gently with the thermometer while observing the temperature (you may want to swirl jar slightly while in contact with table to reach an equilibrium temperature)
9. Turn the power supply on. Record the starting time (t1) and the temperature (T1).
10. Record the current, I, voltage, V, and temperature of water
versus time. Keep an eye on the ammeter and voltmeter throughout
the experiment to be sure these values do not change significantly.
If they do change, use an average value of the power, ![]() ,
in your later calculations.
,
in your later calculations.
11. When the temperature increases about ![]() ,
shut off the power. Be sure to note this time, t2.
Continue stirring or swirling the water gently. Record the thermometer
readings until the temperature peaks, T2 , and starts
to drop. Continue the measurement until the temperature has dropped
several degrees below its maximum.
,
shut off the power. Be sure to note this time, t2.
Continue stirring or swirling the water gently. Record the thermometer
readings until the temperature peaks, T2 , and starts
to drop. Continue the measurement until the temperature has dropped
several degrees below its maximum.
12. Remove the thermometer from the jar. Note how much of the thermometer is immersed in the water. Estimate the volume of thermometer that was immersed.
13. Remove the EEH Jar from the Calorimeter. Weigh the EEH Jar assembly including the water, Mwj.
1) Plot the temperature of the water vs time on linear paper. [You will find this useful later]
2) In order to calculate the electrical equivalent of heat
(Je), you will need to determine both the total electrical
energy (E) that flowed into the lamp and the total heat absorbed
by the water ![]() . The electrical energy
is given by
. The electrical energy
is given by ![]() . The quantity of heat
absorbed by the water, EEH Jar assembly and thermometer is given,
by
. The quantity of heat
absorbed by the water, EEH Jar assembly and thermometer is given,
by ![]() = heat absorbed by water + heat absorbed
by EEH Jar + heat absorbed by thermometer. Then
= heat absorbed by water + heat absorbed
by EEH Jar + heat absorbed by thermometer. Then
![]() (5.15)
(5.15)
where
![]() = mass of water = mass of the jar assembly
with water [Mwj] - mass of the jar assembly alone [Mj]
= mass of water = mass of the jar assembly
with water [Mwj] - mass of the jar assembly alone [Mj]
![]() = specific heat of water =
= specific heat of water = ![]() ,
23
,
23 ![]() is the heat capacity of the jar assembly
alone
is the heat capacity of the jar assembly
alone
![]() is the specific heat of the thermometer.
is the specific heat of the thermometer.
![]() can be written as
can be written as
![]() (5.16)
(5.16)
therefore,
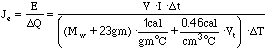 (5.17)
(5.17)
where t = t2 - t1, T = T2 - T1, and Mw = Mwj - Mj.
1. How does your answer for Je compare with the experimental and expected values for J in Part A(mechanical equivalent of heat)? Explain why? (What should you expect for Je?)
2. One of the errors is the loss of heat during the warming
portion of the experiment. From the temperature vs time curve
after the power was shut off, estimate the loss of heat and the
possible error in the value of ![]() that you
determined. Is this a systematic error.
that you
determined. Is this a systematic error.
3. Discuss any other possible errors.
After the light bulb assembly has cooled, you will repeat steps 3 through 13 of 5B.1 without India Ink and Styrofoam Calorimeter. (i.e. You wish to allow visible light to escape.) You will be able to calculate the efficiency of conservation of electrical energy into light. The efficiency of the light bulb is discussed on pg 10.
1) Plot the temperature of water vs time on a linear paper. [You will find this useful later]
2) Find the efficiency of the incandescent lamp as outlined above.
1) Is the incandescent lamp more efficient as a light bulb or as a heater? Explain why?
2) If the power increases, will the efficiency increase?