APPENDIX D

Exponential Decay

Exponential decay occurs whenever a quantity, call it Q(t), changes at a rate,

, (1)

proportional to the value of Q(t) itself. This equation can be integrated (this is an exercise for the reader) to obtain,

, (2)

where = Q(0), the value of Q at t = 0. This characteristic functional evolution accounts for the name: exponential decay.

Figure 1

This is a common type of behavior. Such exponential decay occurs in a wide variety of different physical situations; whenever something changes at a rate proportional to itself.

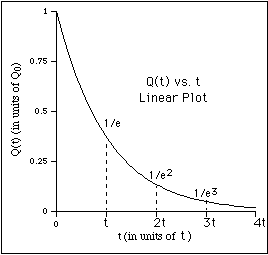
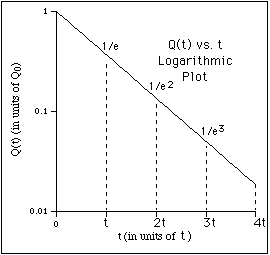
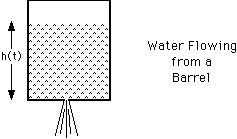
For example, suppose there is a barrel of water with a small hole on the bottom as shown in the figure below. Water will flow out of the hole at a rate proportional to the pressure P of the water at the bottom of barrel. If Q is the volume of water in the barrel, where the constant k depends on things like the size of the hole. Now , where r is the density of water, g is the acceleration of gravity and h(t) is the height of the water at time t. The volume of the water is , where A is the area of the base of the barrel. Therefore, the pressure is proportional to Q(t) and so,

. (3)

Figure 2

This is just the kind of situation under consideration, where the rate of change of a quantity is proportional to itself. Therefore,

(4)

where Q0 is the volume of water in the barrel at time t = 0 and .

It was convenient to write the proportionality constant as 1/t because it is the reciprocal of the constant of proportionality, t, called the time constant or lifetime, which has direct physical significance.

In the case of the water barrel, the lifetime is the time it takes for the water (volume) to drop by a factor of

1/e (~ 0.37). This can be seen by evaluating Q(t) at t = t to obtain,

. (5)

Another useful quantity is called the half-life T1/2. Again, in the case of the water barrel, this is the time it takes the volume of the water to drop to half of what it was at t=0; that is,

. (6)

Taking the logarithm

, (7)

so

, (8)

gives the relation between the time constant and the half-life.

A classic example, where the concepts of lifetime and half-life are commonly used, is the description of radioactive decay. In this case, Q(t) is the number of atomic nuclei at given time. Since the probability of decay per nucleus is a constant, the rate of decrease of the nuclei is proportional to the number of nuclei and the result is exponential decay.

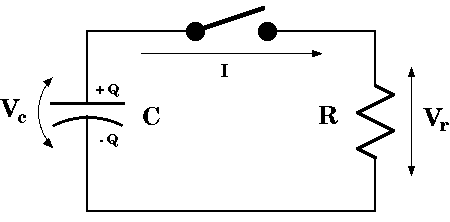
A resistor-capacitor circuit is another example. The voltage on a capacitor is proportional to its charge, . The voltage across a resistor is proportional to the current through it, . If a resistor is connected across an initially charged capacitor (the switch in the diagram is closed) then the charge will flow through the resistor, , and dissipate. Thus, since the voltages across the resistor and capacitor will be equal,

. (9)

This is just exponential decay with a time constant given by t = RC.

Figure 3

Leakage from a charged ball, such as that used in a Coulomb's Law experiment, is another example of exponential decay. The charge will gradually leak off the ball as ions in the air combine with the charges on the ball to neutralize them and/or current flows off through resistive paths (as in the

Figure 4

previous example). Given the density of ions in the air (which will vary with the humidity) the recombination rate of the ions will be proportional to the electric field attracting them to the surface of the ball. And the resistive current flowing off the ball will be proportional to its voltage. But both the electric field at the surface of the ball and the voltage of the ball are proportional to the charge on the ball. Thus the rate at which charge leaks off the ball will be proportional to the charge on the ball and an exponential decay can be expected. The characteristic time constant should depend on the weather conditions and the cleanliness of the apparatus.

In the discussion of exponential decay, it was convenient to think of the independent variable as time. This is often the case, as it was in all the above examples, but the independent variable could be anything.

As a final example of exponential decay, in this instance for a variable that is not time, consider the earth's atmosphere. The pressure at a given height h is given by the perfect gas law

, (10)

in terms of the density r(h) at that height and the average molecular mass M of the atmosphere. But the force of gravity on a small section of the atmosphere

Figure 5

must be balanced by the pressure forces on it if it is to be in equilibrium. For a section of area A and height [Delta]h, then,

, (11)

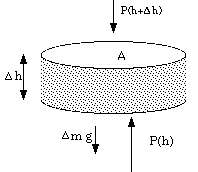
therefore,

, (12)

or, in the limit,

.

This is making the (very poor, in this context!) assumption that the acceleration due to gravity does not depend on height. Combining this with the previous result gives,

, (13)

the rate of change of the pressure with height to be proportional to itself. Thus, the pressure of the atmosphere decays exponentially with height as

, (14)

where is the distance in which the atmospheric pressure decreases by a factor of e and = P(0) is the pressure at h = 0 (say, ground level).

Send comments, questions and/or suggestions via email to wolfs@nsrl.rochester.edu.